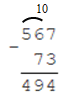Вычитание что это такое в математике
Вычитание натуральных чисел
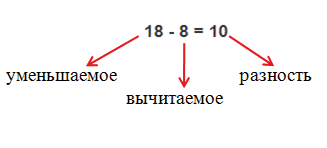
Понятие «вычитание»
Обозначения
Свойства вычитания натуральных чисел
1) При вычитании натуральных чисел уменьшаемое всегда должно быть больше вычитаемого.
2) Разность показывает на сколько больше уменьшаемое больше вычитаемого.
34 больше, чем 7 на 17 единиц.
3) Если вычитаемое равно 0, разность равна уменьшаемому.
4) Если от любого числа вычесть 1, то получим число предшествующее данному.
5) Вычитание натурального числа из суммы натуральных чисел.
Чтобы вычесть натуральное число из суммы натуральных чисел, необходимо сначала сложить числа, а затем вычесть данное натуральное число, или первым действием вычесть данное натуральное число из любого слагаемого, а к разности прибавить оставшееся слагаемое.
6) Вычитание суммы чисел из натурального числа.
Чтобы вычесть сумму чисел из натурального числа, необходимо сначала сложить два числа, после этого вычесть полученную сумму из данного числа, или вычесть из данного числа любое из слагаемых, поле этого вычесть второе.
Вычитание чисел с разными разрядами
Для того чтобы вычесть числа с разным разрядом, необходимо разложить числа по разрядам.
567 = 500 + 60 + 7 = 400 + 100 + 60 + 7
Из единиц вычтем единицы, из десятков десятки, из сотен сотни и т.д.
Поскольку из 60 нельзя вычесть 70, разложим 500 на 400 и 100, прибавим 100 к 60
Полученное число: 400 + 90 + 4 = 494.
Вычитание в столбик
Многозначные числа удобнее всего вычитать в столбик. Для того чтобы вычесть число из числа в столбик, необходимо:
1. Правильно записать числа. Первым записываем уменьшаемое, под уменьшаемым пишем вычитаемое, так чтобы каждый разряд вычитаемого находился строго под соответствующим разрядом вычитаемого. Слева поставим знак «-» под столбиком, состоящим из уменьшаемого и вычитаемого проводим черту
2. Справа налево последовательно вычитаем из разряда уменьшаемого соответствующий разряд вычитаемого. Результат запишем под чертой, это будет разность.
3 Если разряд уменьшаемого окажется меньше разряда вычитаемого занимаем 10 у разряда стоящего слева (см. рисунок).
Вычитание с помощью координатного луча
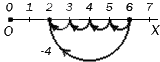
Для вычитания с помощью координатного луча, отметим точку соответствующую уменьшаемому, в нашем примере, это число 12. Для вычитания отсчитываем влево количество единичных отрезков равных вычитаемому (8). Получившаяся точка будет являться разницей (4).
Поделись с друзьями в социальных сетях:
Как найти разность чисел в математике
Содержание:
Само слово «разность» мы часто употребляем в нашей повседневной речи, объясняя им различие чего либо. Например, говоря о различии разных мнений и взглядов можно сказать о «разности» в них. Часто этот термин употребляется в науках, им обозначают разные количественные показатели, скажем разность электрических потенциалов, атмосферного давления или количества сахара в крови человека. Но прежде всего «разность» – это математический термин и об этой его ипостаси мы поговорим в нашей статье.
Арифметические действия с числами
Все основные арифметические действия с числами делятся на четыре большие группы:
Результат каждого из этих действий в свою очередь имеет свое уникальное название:
Роль в математике
Исходя из выше написанного, несложно дать определение того, что такое разность чисел, причем это понятие можно обозначить сразу несколькими способами:
Все эти определение разности являются правильными.
Как найти разность величин
Разность – это результат вычитания одного числа из другого. Первое из этих чисел, с которого делается вычитание, называют уменьшаемым, а второе число называется вычитаемым, его как раз вычитают из первого числа. Итак, чтобы найти значение разности чисел нужно просто от уменьшаемого отнять вычитаемое.
Тут все предельно просто, но при этом у нас появилось еще два дополнительных термина, которые также надо знать:
Итого, для того, чтобы найти разность необходимо знать значение уменьшаемого и вычитаемого, они должны быть известны.
Порой необходимо решить задачу обратную, при известной разности найти уменьшаемое или вычитаемое число. Сделать это тоже просто:
Примеры нахождения
Пример 1. Найти разницу двух величин.
Дано: 20 — уменьшаемое, 15 — вычитаемое.
Решение: 20 — 15 = 5
Ответ: 5 — разница величин.
Пример 2. Найти уменьшаемое.
Дано: 48 — разность, 32 — вычитаемое значение.
Решение: 32 + 48 = 80
Ответ: 80.
Пример 3. Найти вычитаемое значение.
Дано: 7 — разность, 17 — уменьшаемая величина.
Решение: 17 — 7 = 10
Ответ: 10.
И немного более сложных примеров, ведь в математике зачастую высчитывают разность с использованием не только двух, но и гораздо большего количества компонентов, в которых могут быть к тому же не только лишь целые числа, но и дробные, рациональные, иррациональные числа.
Пример 4. Найти разницу трех значений.
Даны целые значения: 56, 12, 4.
56 — уменьшаемое значение, 12 и 4 — вычитаемые значения.
Решение можно выполнить двумя способами.
1 способ (последовательное отнимание вычитаемых значений):
1) 56 — 12 = 44 (здесь 44 — получившаяся разница двух первых величин, которая во втором действии будет уменьшаемым);
2) 44 — 4 = 40.
2 способ (отнимание из уменьшаемого суммы двух вычитаемых, которые в таком случае называются слагаемыми);
1) 12 + 4 = 16 (где 16 — сумма двух слагаемых, которая в следующем действии будет вычитаемым);
2) 56 — 16 = 40.
Ответ: 40 — разница трех значений.
Пример 5. Найти разницу величин 7 и 18.
Дано: 7 — уменьшаемое значение, 18 — вычитаемое.
Вроде все просто, но ведь вычитаемое у нас больше уменьшаемого, как быть в таком случае? В таком случае действует следующее правило: если вычитаемое больше уменьшаемого, то разность окажется отрицательной или другими словами, она будет числом со знаком минус.
Решение: 7 — 18 = —11
Ответ: —11 — отрицательное число со знаком минус.
Вычитание натуральных чисел: правила, примеры и решения
Ранее мы изучали, что такое натуральные числа и какие существуют свойства для того, чтобы производить вычитание. В данной статье представлены основные правила, которые помогут нам выполнять вычитание натуральных чисел. Для того, чтобы информация была понятна и быстро запомнилась, мы снабдили теоретический материал подробно разобранными упражнениями и типичными примерами.
Как связаны сложение и вычитание
Сложение и вычитание тесно связаны. Вычитание – это действие, обратное для сложения. Чтобы усвоить эту информацию, следует рассмотреть подробный пример.
Преобразуем данное утверждение и получим важное правило.
Теперь мы можем отчетливо увидеть, что сложение и вычитание неразрывно связаны. Исходя из этого факта, можно вывести понятие.
Вычитание – это действие, с помощью которого находится одно слагаемое, когда известна сумма и другое слагаемое.
Данное определение зачастую применяется в различных примерах и задачах.
Как выполнять вычитание с помощью таблицы
Таблица сложения зачастую может быть использована для нахождения суммы двух чисел и для нахождения одного слагаемого в том случае, если известна сумма и другое слагаемое.
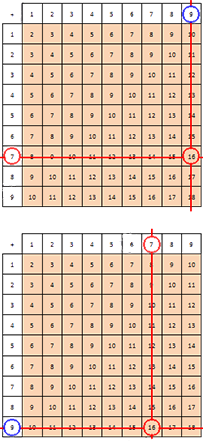
Это может быть выполнено двумя способами. Воспользуемся графической иллюстрацией, на которой известные числа выделены красным, а найденные – синим.
Рассмотрим несколько способов.
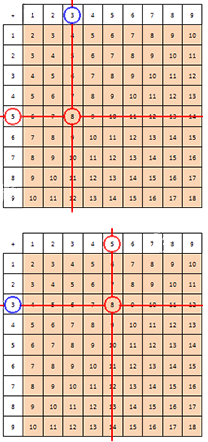
Первый способ. Необходимо найти строку в таблице, известное слагаемое расположено в крайней левой ячейке (берем известное число 5 ). После этого необходимо найти столбец, пересекающийся с найденной строкой в ячейке. Эта строка должна содержать известную сумму (согласно примеру, число 8 ). Число, которое нам необходимо найти, расположено в верхней ячейке найденного столбца. Делаем вывод, что число 3 – это и есть искомое слагаемое.
Второй способ. Необходимо найти в таблице сложения столбец, в верхней ячейке которого располагается известное слагаемое. Находим строчку, пересекающуюся с известным столбцом в ячейке, который соответствует известной сумме. Делаем вывод, что слагаемое, которое требуется найти, расположено в крайней левой ячейке этой строки.
Так, как мы знаем, что сложение и вычитание тесно связаны, эта таблица может быть использована и для поиска разности натуральных чисел. Подробно рассмотрим данную теорию на примере.
Для того, чтобы пользоваться данной таблицей, рекомендуем заучить информацию и довести процесс нахождения чисел по таблице до автоматизма.
Как производить вычитание разрядов чисел
Если вспомнить, что одна сотня – это 10 десятков, одна тысяча – это 10 сотен, то мы можем вычислять разность, десятков, сотен, тысяч и других чисел.
Вычитание натурального числа из суммы чисел
Чтобы найти разность суммы двух чисел и числа, необходимо сначала вычислить сумму, из которого вычитается число. Чтобы упростить процесс вычитания, можно воспользоваться определенным свойством вычитания. Рассмотрим несколько примеров.
Вычитание суммы чисел из натурального числа
Чтобы вычесть сумму двух чисел из натурального числа, необходимо вычислить сумму, после чего провести вычитание.
Можно использовать свойство вычитания, приведенное выше. Рассмотрим несколько примеров.
Используя свойство вычитания и сочетательное свойство сложения, можно найти разность суммы двух, трех и более чисел.
Краткая запись решения имеет вид: 1 000 − ( 900 + 90 + 1 ) = ( 1 000 − 900 ) − ( 90 + 1 ) = 100 − ( 90 + 1 ) = ( 100 − 90 ) − 1 = 10 − 1 = 9
Вычитание единиц из десятков, сотен, тысяч
Рассмотрев вычитание единиц из десятков, перейдем к вычитанию единиц из сотен.
Чтобы из 100 вычесть число от 1 до 10 нужно 100 представить, как 90+10 90 + 10 и прибегнуть к правилу.
Перейдем к вычитанию единиц из тысяч.
Необходимо вычесть из 7 000 единицу.
Используя данный пример, мы сможем вычитать любые числа, также тысячные и десятитысячные.
Вычитание единиц из произвольных чисел
Будем считать, что уменьшаемое можно представить в виде суммы разрядных слагаемых. Подобные случаи мы рассматривали в предыдущих параграфах.
Чтобы вычесть из такого числа однозначное число, нужно уменьшаемое разложить по разрядам, после чего вычесть число из суммы.
Рассмотрим типичные примеры, которые помогут усвоить материал.
Закрепим навыки еще одним примером.
Вычитание из произвольных натуральных чисел
Чтобы вычесть десятки, сотни из числа, нужно уменьшаемое представить как сумму и выполнить вычитание. Разберем данный процесс на нескольких примерах.
Пользуемся этим правилом в аналогичных случаях.
Воспользуемся схожим принципов для вычисления сотен, тысяч и других.
Данное правило можно использовать для вычисления. Запомнить его, оно еще не раз вам пригодится.
Вычитание произвольных чисел
Рассмотрим правило, когда вычитаемое раскладывается по разрядам. После представления числа в виде суммы разрядных слагаемых используется свойство вычитания, описанное выше. Вычитание начитается с единиц, потом десятков, сотен и так далее.
Усвоив предыдущие правила, вы легко выполните это.
Все решение удобно записывать в виде цепочки равенств:
45 − 32 = 45 − ( 2 + 30 ) = ( 45 − 2 ) − 30 = ( ( 40 + 5 ) − 2 ) − 30 = = ( 40 + ( 5 − 2 ) ) − 30 = ( 40 + 3 ) − 30 = ( 40 − 30 ) + 3 = 10 + 3 = 13
Немного усложним пример.
Тогда ( 85 − 8 ) − 10 = 77 − 10 = ( 70 + 7 ) − 10 = ( 70 − 10 ) + 7 = 60 + 7 = 67
Для закрепления материала разберем решение еще одного примера.
Вычитание чисел на координатном луче
Проверка результата вычитания сложением
Теперь мы можем сформулировать правило, позволяющее проверить результат вычитания сложением: нужно к полученной разности прибавить вычитаемое, при этом должно получиться число, равное уменьшаемому. Если полученное число не равно уменьшаемому, то при вычитании допущена ошибка.
Осталось лишь разобрать решения нескольких примеров, в которых выполняется проверка результата вычитания при помощи сложения.
Необходимо определить разность 1 024 − 11 и проверить результат.
Теперь выполняем проверку:
1 013 + 11 = ( 1 000 + 10 + 3 ) + ( 10 + 1 ) = = 1 000 + 10 + 10 + 3 + 1 = 1 000 + 20 + 4 = 1 024
Проверка результата вычитания вычитанием
Правильность результата вычитания натуральных чисел можно проверить не только с помощью сложения, но и с помощью вычитания. Для этого нужно от уменьшаемого отнять найденную разность. При этом должно получиться число, равное вычитаемому. В противном случае в вычисления была допущена ошибка.
Это число равно вычитаемому, вычитание выполнено верно.
Вычитание натуральных чисел: свойства, примеры
Операции вычитания между любыми натуральными числами присущ ряд особенностей, называемых свойствами. В данной статье мы рассмотрим основные свойства натуральных чисел и приведем разъясняющие примеры.
Свойство вычитания равных натуральных чисел
Это самое простое свойство. Число ноль указывает на отсутствие чего либо. Если из множества каких-то объектов вычесть такое же множество объектов, получится ноль. Например, у Пети было 15 яблок, он решил угостить Машу и отдал ей все 15 штук. Теперь у Пети ноль яблок.
Переместительный закон (не выполняется для вычитания)
Известно, что при сложении чисел от перемены мест слагаемых сумма не меняется. Так же, как и при умножении произведение не меняется при перестановке множителей. Эта особенность называется переместительным, или коммутативным законом. Однако при вычитании коммутативный закон работает только в одном случае: когда вычитаемое число равно уменьшаемому.
В случаях, когда уменьшаемое число становится меньше вычитаемого, теряется сам смысл вычитания натуральных чисел. Например:
Свойства вычитания натуральных чисел
Для операции вычитания натуральных чисел переместительный закон не выполняется!
Вычитание суммы двух чисел из натурального числа
Сформулируем свойство, а затем рассмотрим пример, который даст глубокое понимание и поможет осмыслить сказанное.
Свойство вычитания суммы двух чисел из натурального числа
Вычитание суммы двух натуральных чисел из другого натурального числа равносильно последовательному вычитанию из числа сначала одного слагаемого суммы, а затем другого.
Математически это запишется так:
Обратимся к примеру. У Пети и у Васи было по 8 монет. Петя сразу купил напиток за две монеты и конфету за одну монету. Вася сначала купил напиток, а потом подумал, и тоже купил конфету. В итоге, у обоих осталось по пять монет. Операции с монетами Пети и Васи можно соответственно записать так:
Важно отметить, что данная операция для натуральных чисел имеет смысл только тогда, когда уменьшаемое число больше или равно сумме чисел, которые из него вычитают.
В соответствии с рассмотренным свойством и сочетательным законом, можно вычитать из натурального числа сумму двух, трех и более чисел.
Вычитание числа из суммы
Количество конфет в итоге остается неизменным и справедливы равенства:
Теперь можно сформулировать правило вычитания числа из суммы других натуральных чисел.
Свойство вычитания натурального числа из суммы двух чисел
Вычитание натурального числа из суммы других натуральных чисел эквивалентно последовательному вычитанию данного числа из одного слагаемого и сложению полученной разности с другим слагаемым.
В буквенной форме свойство имеет следующий вид:
Свойство вычитания натурального числа из суммы трех и более чисел формулируется аналогично и вытекает из свойства вычитания числа из суммы двух чисел.
Пример. Вычитание числа из суммы
Как найти разность чисел в математике?
Вычесть значит отнять одно число от другого. Вычитание есть такое действие, в котором отнимают меньшее число от большего. При вычитании целых чисел большее число уменьшается на столько единиц, сколько их содержится в меньшем.
Вычитание
В вычитании два данных числа называются уменьшаемым и вычитаемым, а искомое — разностью.
Уменьшаемым называют большее число, от которого отнимают другое. Оно уменьшается от вычитания.
Вычитаемым называют меньшее число, которое отнимают от большего.
Разностью называют вывод, полученный от вычитания. Разность определяет, чем одно число больше другого или показывает разницу между двумя числами.
Знак вычитания. Действие вычитания обозначается знаком — (минус).
Вычитание однозначных чисел
Чтобы обозначить, что из 9 нужно вычесть 6, пишут эти числа рядом, отделяя их знаком — (минус):
Разность между этими числами будет 3, и ход вычисления выражают словесно:
девять без шести равно трем.
Большее число 9 будет уменьшаемым, меньшее 6 вычитаемым, число 3 остатком.
Способы вычитания
Можно двумя способами вычесть одно число из другого:
Число единиц, которое нужно прибавить к меньшему числу, чтобы уравнять его с большим, определяет разность.
Меньшее число с разностью должно равняться большему числу, следовательно, меньшее число и разность суть слагаемые, а большее — их сумма. На этом основано другое определение вычитания:
В этом случае данная сумма есть уменьшаемое, данное слагаемое — вычитаемое, а искомаяразность — другое слагаемое.
Вычитание многозначных чисел
Вычитание многозначных чисел основывается на том свойстве чисел, по которому вычесть число все-равно, что вычесть все его части. Из этого свойства видно, что вычесть какое-нибудь число все-равно, что вычесть последовательно все его единицы, десятки, сотни и т. д. Чтобы обозначить, что из числа 7228 нужно вычесть 3517, пишут:
Чтобы облегчить вычитание, подписывают меньшее число под большим так, чтобы единицы одинаковых порядков находились в одном вертикальном столбце, проводят черту, слева ставят знак вычитания — и под чертою подписывают разность.
Ход вычисления выражают словесно:
Ход вычисления выражают письменно:
Пример. Из 17004 вычесть 6025.
Из 4 нельзя вычесть 5. Занимаем единицу у десятков, следующего высшего порядка, но в этом порядке единиц нет; занимаем у сотен, — и сотен нет; занимаем у тысяч и обозначаем это точкой над цифрой 7.
Единица четвертого имеет 10 единиц третьего порядка. Взяв из них одну для десятков, оставляем их в сотнях только 9. Присоединив 10 к 4, имеем 14.
Производя вычитание, получим:
Для десятков тысяч имеем 1, ибо эту цифру уменьшаемого переносим в разность без изменения.
Ход вычисления выразится письменно:
Из предыдущих примеров выводим правила вычитания:
Зависимость между данными и искомыми вычитания
Из примера 9 — 6 = 3 видно, что
Арифметическое дополнение. Разность между числом и ближайшей большей единицей называется арифметическим дополнением. Так, арифметическими дополнениями чисел 7, 79, 983 будут числа:
Арифметическим дополнением иногда пользуются для облегчения арифметических вычислений.
Вычитание чисел
Вычитание – это арифметическое действие обратное сложению, посредством которого из одного числа вычитают (отнимают) столько единиц, сколько их содержится в другом числе.
Число, из которого вычитают, называется уменьшаемым, число, которое указывает сколько единиц будет вычтено из первого числа, называется вычитаемым. Число, получаемое в результате вычитания, называется разностью (или остатком).
Рассмотрим вычитание на примере. На столе лежит 9 конфет, если съесть 5 конфет, то их останется 4. Число 9 является уменьшаемым, 5 – вычитаемым, а 4 – остатком (разностью):
Для записи вычитания используется знак — (минус). Он ставится между уменьшаемым и вычитаемым, при этом уменьшаемое записывается слева от знака минус, а вычитаемое – справа. Например, запись 9 — 5 означает, что из числа 9 вычитается число 5. Справа от записи вычитания ставят знак = (равно), после которого записывают результат вычитания. Таким образом, полная запись вычитания выглядит так:
Эта запись читается так: разность девяти и пяти равняется четырём или девять минус пять равно четыре.
Чтобы в результате вычитания получить натуральное число или 0, уменьшаемое должно быть больше вычитаемого или равно ему.
Рассмотрим, как, используя натуральный ряд, можно выполнить вычитание и найти разность двух натуральных чисел. Например, нам необходимо вычислить разность чисел 9 и 6, отметим в натуральном ряду число 9 и отсчитаем от него влево 6 чисел. Получим число 3:
Вычитание также можно использовать для сравнения двух чисел. Желая сравнить между собой два числа, мы задаёмся вопросом, на сколько единиц одно число больше или меньше другого.
Чтобы узнать это, надо из большего числа вычесть меньшее. Например, чтобы узнать, на сколько 10 меньше 25 (или на сколько 25 больше 10), надо из 25 вычесть 10.
Тогда найдём, что 10 меньше 25 (или 25 больше 10) на 15 единиц.
Проверка вычитания
где 15 – это уменьшаемое, 7 – это вычитаемое, а 8 – разность. Чтобы узнать правильно ли было выполнено вычитание, можно:
Что такое разность чисел в математике?
Для многих точные науки, вроде математики, воспринимаются как нечто более простое, чем сферы, требующие рассуждений, предполагающие большую вариативность. Однако все предметы имеют свои сложности, в том числе и технические.
Вычитание
Для того, чтобы понять, чем является разность, необходимо разобраться в ряде математической терминологии. В первую очередь, нужно выяснить, чем является вычитание.
По-другому это понятие называют убавлением, и по такому названию понять смысл процесса несколько проще. По своей сути вычитание является одной из математических операций.
Что же это за операции? Как правило, под ними понимают определенные арифметические или логические действия. Встает логичный вопрос – в чем же суть арифметических действий?
Понятие арифметики появилось достаточно давно. Оно зародилось в древнегреческом языке, где переводилось как «число». Сегодня это раздел математики, который изучает числа, их отношения друг к другу, а также свойства.
Итак, вычитание – это операции с числами, относящиеся к бинарным. Суть бинарных операций в том, что в них используются два аргумента (параметра), и получается один результат.
Стоит рассмотреть, как найти разность какого-то числа. В первую очередь, необходимы два аргумента, то есть два числа. Затем необходимо уменьшить значение первого числа на значение второго.
Когда данная операция выражается письменно, используется знак «минус». Это выглядит так: а – б = с, где а является первым числовым значением, б – вторым, а с – разностью чисел.
Как правило, у учеников возникает гораздо больше проблем именно с вычитанием, нежели со сложением. Отчасти это связано со свойствами данных математических операций.
Всем известно, что от перемены мест слагаемых значение суммы не меняется. В вычитании же всё гораздо сложней. Если поменять числа местами, получится совершенно другой результат.
Схожим свойством в прибавлении и убавлении является то, что нулевой элемент не меняет исходное число.
В вычитании всё относительно просто, если первое число больше второго, однако в школе будут рассматриваться и противоположные примеры. В этом случае возникает понятие отрицательного числа.
Например, если нужно вычесть из 5 число 2, то всё несложно. 5-2=3, таким образом разность числа составит 3. Однако, что делать, если необходимо посчитать, сколько будет два минус пять?
В выражении 2-5 разность уйдет в минус, то есть в отрицательное значение. Из двойки легко можно вычесть двойку, получив таким образом ноль, однако от пятерки остается ещё три. Таким образом, результатом данного выражения будет отрицательное число три. То есть, 2-5=-3.
Что такое разность чисел: уменьшаемое, вычитаемое, разность — правило
Статья познакомит читателя с понятиями «разность чисел», «вычитаемое» и «уменьшаемое».
В арифметике существует всего четыре основных действия, которые мы называем сложением, умножением, вычитанием и делением.
Такие действия являются основой всей математики – они позволяют нам осуществлять все вычисления: как простые, так и самые сложные.
Самыми простыми действиями считаются сложение и вычитание, которые противоположны друг другу. Правда, слово «сложение» мы также используем и в обычной жизни.
Мы можем встретить фразу «сложить усилия, например, когда нам нужно сделать какую-нибудь работу всем вместе. Но вот с термином «вычитание» дело обстоит немного сложнее, и в разговоре оно встречается реже.
Мы редко услышим такие выражения, как «уменьшаемое», «вычитаемое», «разность». Но в сегодняшней статье мы подробно поговорим о них с точки зрения математики.
Что значит число уменьшаемое, число вычитаемое и разность чисел?
Что значит число уменьшаемое, число вычитаемое и разность чисел? Как известно, многие научные термины и выражения взяты из других языков, чаще греческого и латинского. Но те слова, которые будут рассмотрены ниже, имеют русское происхождение, потому нам будет проще их разобрать.
Например, что можно сказать о разности чисел? Если мы обратим внимание на корень слова «разность», то нам представится, например, его однокоренное слово «разница».
А если речь идет о математике, то тут и думать нечего – слово «разность» означает разницу между какими-то цифрами, а точнее, двумя числами.
Разница нам показывает, насколько одна величина больше другой или, наоборот, вторая меньше первой. Строго в математике это выглядит как результат вычитания.
Сразу же приведем пример. Допустим, буфетчица несет на подносе восемь пирожков. Пять из них она раздала посетителям. Сколько пирожков останется у буфетчицы на подносе? Если из 8 вычесть 5, то получится — 3. Теперь запишем это математически:
То есть разница между восемью и пятью – это три. Теперь нам понятно, что такое термин «разница».
Внимание: Если два числа равны друг другу, то разницы между ними не существует, она равна нулю (8 – 8 = 0).
Теперь нам следует выяснить, что такое вычитаемое и уменьшаемое. Снова представим значение слов по их смыслу. Чем может являться число уменьшаемое? Уменьшаемое – это то число, которое уменьшается при вычитании. От этого числа отнимают другое число. А что такое вычитаемое? Вычитаемым как раз и является том числом, которые мы отнимаем от уменьшаемого.
Вернемся к примеру с буфетчицей. Мы помним, как от восьми отнимали пять, и у нас получилось три. Мы выяснили, что тройка является разницей между двумя этими числами. Теперь нам уже не сложно понять, что 8 – это число уменьшаемое, а 5 – это число вычитаемое.
Как найти уменьшаемое и вычитаемое число?
Как в математике найти разницу чисел мы уже разобрались. Это довольно просто. Но сможем ли мы найти уменьшаемое и вычитаемое число, если одно число неизвестно? Конечно можем, так как нам будут известны два других числа. Например, как мы можем найти уменьшаемое число? Если мы знаем значение разницы и вычитаемого, то сумма этих двух чисел равняется уменьшаемому:
Вычитаемое находится так же просто. Если мы знаем разницу и уменьшаемое, значит вычитаемое мы получим, отняв от уменьшаемого числа разность:
Что такое разность чисел в математике и как найти разность чисел
В этой статье мы рассмотрим, что такое разность чисел в математике, и как человеку, интересующемуся этой наукой, найти разность чисел.
Что такое разность чисел в математике
Вычитание является одной из 4 арифметических операций. Для его обозначения служит математический знак «−» (минус). Вычитание противоположно по смыслу операции сложения.
Операция вычитания в общем случае записывается следующим образом:
Число Математическое название
| A | Уменьшаемое |
| B | Вычитаемое |
| C | Разность чисел |
Здесь разностью чисел будет являться число 4. Следовательно, разность между любыми числами A и B это такое число C, которое при прибавлении к B даст в сумме A (4 при прибавлении к 2 дает 6 — значит, 4 это разность 6 и 2).
Как найти разность чисел
Уже из самого определения следует, как вычислить разность между двумя числами. При небольших числах можно делать это в уме. Детей в начальной школе учат следующим образом. Представьте, что у Вас есть 5 яблок, и 3 из них забрали. Сколько у Вас осталось? Правильно — 2 яблока. Постепенно Вы доведете вычисления до автоматизма и будете сразу выдавать ответ.
Однако для чисел выше 50 такое наглядное представление перестает работать. Большое количество предметов тяжело представить в уме, поэтому здесь на помощь приходит другой способ:
Вычисление разности в столбик
Школьники изучают этот способ в рамках курса математики, обычно во втором или третьем классе. Взрослые люди, пользующиеся калькулятором, зачастую забывают, как считать в столбик. Однако калькулятор не всегда бывает под рукой. Освежите в памяти школьные знания, посмотрев это видео.
Вычисление разности в столбик – видео
Этот способ применим и тогда, когда Вам нужно вычесть большее число из меньшего. В реальной жизни такое обычно не требуется, но может пригодиться при решении математических задач.
Допустим, в примере «A − B = C» B больше, чем A. Тогда C будет отрицательным. Чтобы вычислить разность, «разверните» пример: посчитайте значение B − A.
Когда Вы закончите считать эту разность, у вас получится число C, только с противоположным знаком: оно будет больше нуля. Чтобы завершить вычисления, припишите к нему спереди знак минус.