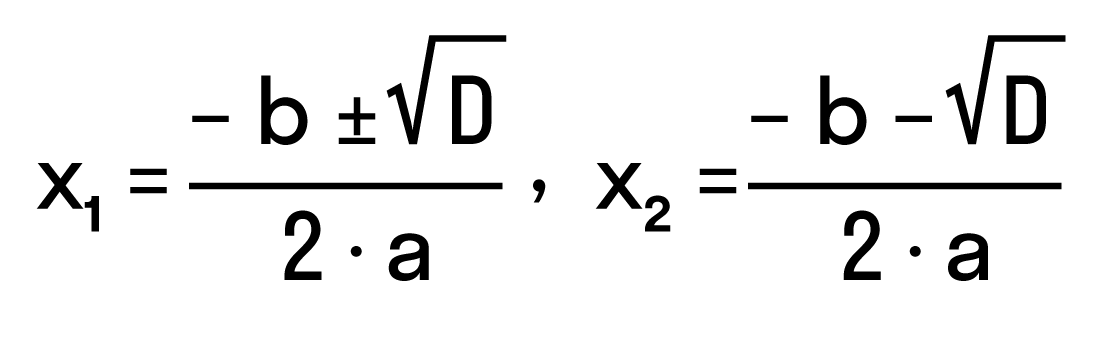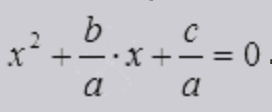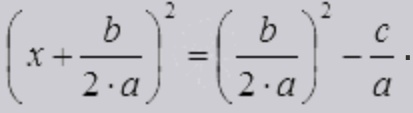квадратные уравнения какой класс
Разработка раздела образовательной программы по теме «Квадратные уравнения»
Ищем педагогов в команду «Инфоурок»
Муниципальное бюджетное общеобразовательное учреждение
Методическая разработка раздела
образовательной программы по математике
«Квадратные уравнения» (8 класс)
Выполнила учитель математики
МБОУ Велетьминской школы
Тюрина Нина Александровна
Психолого-педагогическое объяснение специфики восприятия и освоения учебного материала учащимися в соответствии с возрастными особенностями……………………..5
Психолого-педагогические особенности подросткового возраста…………………. 6
Уровни усвоения учебной информации у подростков………………………………. 6
Ожидаемые результаты освоения раздела программы………………………………………7
Обоснование используемых в образовательном процессе по разделу программы образовательных технологий, методов, форм организации деятельности учащихся………………………………………………………………………………………..8
Система знаний и система деятельности……………………………………………………11
Календарно–тематическое планирование по разделу «Квадратные уравнения»………. 13
Результаты апробации содержания раздела «Квадратные уравнения»…………………..19
Методическая разработка образовательного раздела «Квадратные уравнения» предназначена для обучающихся 8 класса, составлена на основе
Программы. Математика. 5-6 классы. Алгебра. 7-9 классы. Алгебра и начала анализа. 10-11 классы/ авт. – сост. И.И. Зубарева, А.Г. Мордкович. – М.: Мнемозина, 2009.
Алгебра. 8 класс. В 2ч. Ч.1. Учебник для учащихся общеобразовательных учреждений / А.Г. Мордкович. – 11–е изд., испр. – М.: Мнемозина, 2009.
Алгебра. 8 класс. В 2ч. Ч.2. Задачник для учащихся общеобразовательных учреждений / [А.Г. Мордкович и др.]; под ред. А.Г. Мордковича. – 11-е изд., испр. и доп. – М.: Мнемозина, 2009.
Раздел «Квадратные уравнения» изучается во втором полугодии, на формирование основных понятий по данному разделу отводится 21 час. Изложение учебного материала в учебниках данных авторов в основном достаточно традиционно. Учащиеся должны: научиться решать полные квадратные уравнения выделением квадрата двучлена, графически, по общей формуле и формуле с четным вторым коэффициентом; знать виды уравнений (полное, неполное, приведенное, неприведенное); уметь решать неполные квадратные уравнения, рациональные, биквадратные; раскладывать квадратный трехчлен на множители; применять теорему Виета; решать текстовые задачи с помощью квадратных уравнений.
Раздел программы содействует сохранению единого образовательного пространства, не сковывая творческой инициативы учителя, предоставляет широкие возможности для реализации различных подходов к построению учебного курса с учетом индивидуальных способностей и потребностей учащихся, материальной базы школы. Темы занятий в планировании распределены по принципам: систематичности, последовательности, доступности.
Цели и задачи раздела «Квадратные уравнения»
Цель: освоение учащимися понятий квадратное уравнение, полное и неполное квадратное уравнение, формирование умений решать квадратные уравнения различными способами, решать задачи, в которых математической моделью являются квадратные уравнения.
продолжение формирования центральных математических понятий;
обеспечить усвоение знаний и правильное употребление терминов, связанных с квадратными уравнениями;
ознакомить с алгоритмом нахождения корней квадратного уравнения;
формирование навыков решения квадратных уравнений различными способами и выработка умений выбрать научный, рациональный способ решения уравнения;
ознакомить с алгоритмом решения рациональных и иррациональных уравнений;
научить использовать квадратные уравнения при решении математических и практических задач;
научить переносить приобретенные знания на другие области (геометрия, физика, химия).
развитие логического мышления, памяти, внимания;
развивать у школьников умение выделять главное в изучаемом материале, учить анализировать, сравнивать, строить аналогии, обобщать и систематизировать полученные знания;
развитие интеллектуальных и творческих способностей учащихся, познавательной активности, интереса к изучению математики;
овладение математическими знаниями и умениями, необходимыми для применения в повседневной жизни.
воспитание математической культуры обучающихся;
воспитание качеств личности, необходимых человеку для развития его способностей, в том числе коммуникативных.
Психолого-педагогическое объяснение специфики восприятия и освоения учебного материала обучающимися в соответствии с возрастными особенностями
Для того чтобы развивать познавательную деятельность обучающихся, формировать интерес к процессу познания необходимо учитывать индивидуальные особенности ребенка.
В 8 классе обучается 7 человек: 6 девочек и 1 мальчик. Рассматривая отношение обучающихся к учебной деятельности, можно выделить следующие группы ребят:
У двоих обучающихся высокий уровень развития. Отношение к учёбе положительное, активное, инициативное. Умеют анализировать, сравнивать, делать выводы самостоятельно. Речь хорошо развита, большой словарный запас. Для них характерны мотивы совершенствования способов учебно-познавательной деятельности. Они понимают связь результатов деятельности со своими возможностями, применяют знания в знакомых условиях.
У троих обучающихся средний уровень развития. У них преобладает механическая память. Речь хорошо развита, большой словарный запас. Они не сразу усваивают учебный материал. Эти дети не умеют анализировать, сравнивать, обобщать, находить различия. Понимают и выполняют учебные задачи, но рассуждают и делают выводы с помощью учителя.
У двоих обучающихся низкий уровень развития. У них непроизвольное внимание, отсутствует способность к длительной и стойкой сосредоточенности, быстро появляется утомление. Эти дети нуждается в постоянном контроле со стороны учителя. Речь развита слабо, есть недостатки в произношении, часто затрудняются выражать свои мысли, задания выполняют только по образцу.
В эмоционально-волевой сфере класс в целом уравновешенный.
Для обучающихся 8 класса, продолжающих изучение математики, актуальной является задача, связанная с развитием и поддержанием устойчивого интереса к предмету. По отношению ко всем обучающимся важно решение задач, связанных с развитием таких качеств, как самостоятельность, инициативность, самооценка, умение работать в коллективе, развитие общеучебных умений, осознания возможности, развития у обучающихся умения выражать личностное отношение к воспринимаемой информации.
Психолого – педагогические особенности подросткового возраста
Быстрый рост, развитие и перестройка организма ребенка
Активный интерес к познанию
Увеличение объема памяти, избирательность внимания
Активное усвоение и развитие мыслительных операций
Формирование активного самостоятельного, творческого мышления.
Стремление к познанию, активность, инициативность, упорство в достижении цели.
Уровни усвоения учебной информации у подростков
Алгебра и начала математического анализа. 10 класс
Конспект урока
Алгебра и начала математического анализа, 10 класс
Урок №3. Квадратные уравнения, неравенства и их системы.
Перечень вопросов, рассматриваемых в теме:
Ткачева М. В., Федорова Н. Е. Алгебра и начала математического анализа. Тематические тесты. 10 класс. Базовый и профильный уровни. 2016.
Шабунин М. И., Ткачева М. В., Фёдорова Н.Е. и др. Алгебра и начала математического анализа. Дидактические материалы. 10 класс. Профильный уровень. 2016.
Теоретический материал для самостоятельного изучения
В курсе средней школы будут рассматриваться показательные, логарифмические, тригонометрические уравнения и неравенства. Чтобы облегчить дальнейшее изучение специальных уравнений, нужно уметь решать квадратные уравнения и неравенства, устанавливать и объяснять зависимость вида решения от его коэффициентов и дискриминанта, представлять геометрическую интерпретацию задач.
На уроке будем рассматривать различные способы решения квадратных уравнений.
Как определить, сколько корней имеет уравнение, подскажет дискриминант.
Дискриминант – это число, которое находим по формуле
Если D 0 два корня.
Рассмотрите пример. Решить уравнение
Шаг 1. Выпишем коэффициенты a, b, c.
Шаг 2. Найдем дискриминант. D=16.
Шаг 3. Запишем формулу корней и подставим значения. Вычислим значения корней:
1.Перед решением квадратного уравнения привести его к стандартному виду.
3. Если в уравнении есть дробные коэффициенты, умножьте уравнение на общий знаменатель.
4. Проверяйте корни по теореме Виета. Это просто, когда a=1.
Рассмотрите другие формулы:

Приведенное квадратное уравнение 
Уравнение (х-3) (х+5) =0 является квадратным. Для его решения воспользуйтесь свойством: произведение равно 0, когда один из множителей равен 0.
Осталось вспомнить, как решаются неполные квадратные уравнения. Неполные — значит один или два коэффициента равны нулю.
Для решения систем уравнений применяются все методы решения: подстановки, сложения, графический.
Рассмотрим несколько примеров:
Если из одного из уравнений можно выразить х или у, применяем метод подстановки. Выразите х из первого уравнения и подставьте во второе. Решите и найдите корни.
Применяем метод сложения. Выполнив сложение, получаем уравнение 
Пример 3. Иногда проще ввести новые переменные.
Пусть xy=u, x+y=v. Тогда систему можно записать в более простом виде:
Решение смотри в примере 1.
Часть 2. Квадратные неравенства.
Теперь, когда мы разобрали решение квадратных уравнений, переходим к решению квадратных неравенств
ax^2+ bx + c больше или меньше нуля.
Шаг 1. Запишем соответствующее неравенству квадратное уравнение и найдем его корни. Отметим корни на оси OХ и схематично покажем расположение ветвей параболы «вверх» или «вниз».
Шаг 2. Расставим на оси знаки, соответствующие знаку квадратичной функции: там, где парабола выше оси, ставим +, а там, где ниже –.
Шаг 3. Выписываем интервалы, соответствующие знаку неравенства. Если неравенство нестрогое, корни входят в интервал, если строгое не входят.
Вспомните возможные случаи расположения корней на оси и ветвей параболы в зависимости от коэффициента а и дискриминанта.
Метод интервалов упрощает схему решения. По-прежнему находим корни квадратного трехчлена, расставляем на числовой прямой. Определяем знаки на интервалах + или – по схеме:
Далее рассмотрим схему решения системы неравенств.
Алгоритм решения системы неравенств.
1.Решить первое неравенство системы, изобразить его графически на оси x.
2.Решить второе неравенство системы, изобразить его графически на оси x.
3.Выбрать в ответ те участки, в которых решение первого и второго неравенств пересекаются. Записать ответ.
Теперь, когда мы разобрали решение квадратных уравнений и неравенств переходим к решению самых сложных заданий с параметрами. Если в уравнении или неравенстве некоторые коэффициенты заданы не числовыми значениями, а обозначены буквами, то они называются параметрами, а само уравнение или неравенство параметрическим.
Второй шаг – определить допустимые значения.
Если в задаче требуется определить знаки корней квадратного уравнения, то, как правило, удобнее использовать теорему Виета.
Но прежде, чем применять теорему Виета, обязательно нужно проверить, что уравнение имеет корни! Для этого вычисляем дискриминант.
Рассмотрите примеры решения неравенства с параметром.
Графический метод решения обладает несомненным преимуществом – можно представить решение наглядно.
Для любого свойства, сформулированного на алгебраическом языке, нужно уметь давать геометрическую интерпретацию и, наоборот, по поведению графика параболы дать общую оценку коэффициентов квадратного трехчлена и его корней.
Например, если старший коэффициент квадратного трехчлена меньше 0, то ветви параболы направлены вниз. Если дискриминант больше 0, то трехчлен имеет различные действительные корни и парабола пересекает ось абсцисс в двух точках и т.д.
Мы рассмотрели лишь некоторые примеры, иллюстрирующие применение графического метода к решению квадратных уравнений и неравенств. Более подробно с методами решения квадратных уравнений, неравенств, их систем вы можете, поработав с интерактивными моделями.
Задания тренировочного модуля с разбором.
При каких значениях параметра, а квадратное уравнение

Находим дискриминант D=25-4∙2∙5a=25-40a. Уравнение имеет один корень, если D=0, т.е. 25-40a=0, а=5/8.
Определите, на каком интервале значения квадратного трехчлена 
Решаем неравенство: 

Как решать квадратные уравнения
Понятие квадратного уравнения
Уравнения — это математическое равенство, в котором неизвестна одна или несколько величин. Значения неизвестных нужно найти так, чтобы при их подстановке в пример получилось верное числовое равенство.
Например, возьмем выражение 3 + 4 = 7. При вычислении левой части получается верное числовое равенство, то есть 7 = 7.
Уравнением можно назвать выражение 3 + x = 7, с неизвестной переменной x, значение которой нужно найти. Результат должен быть таким, чтобы знак равенства был оправдан, и левая часть равнялась правой.
Степень уравнения можно определить по наибольшей степени, в которой стоит неизвестное. Если неизвестное стоит во второй степени — это квадратное уравнение.
Квадратное уравнение — это ax2 + bx + c = 0, где a — первый или старший коэффициент, не равный нулю, b — второй коэффициент, c — свободный член.
Чтобы запомнить месторасположение коэффициентов, давайте потренируемся определять их.
Есть три вида квадратных уравнений:
Чтобы определить, сколько корней имеет уравнение, нужно обратить внимание на дискриминант. Чтобы его найти, берем формулу: D = b 2 − 4ac. А вот свойства дискриминанта:
С этим разобрались. А сейчас посмотрим подробнее на различные виды квадратных уравнений.
Приведенные и неприведенные квадратные уравнения
Квадратное уравнение может быть приведенным или неприведенным — все зависит от от значения первого коэффициента.
Приведенное квадратное уравнение — это уравнение, где старший коэффициент, тот который стоит при одночлене высшей степени, равен единице.
Неприведенным называют квадратное уравнение, где старший коэффициент может быть любым.
Давайте-ка на примерах — вот у нас есть два уравнения:
В каждом из них старший коэффициент равен единице (которую мы мысленно представляем при x 2 ), а значит уравнение называется приведенным.
Каждое неприведенное квадратное уравнение можно преобразовать в приведенное, если произвести равносильное преобразование — разделить обе его части на первый коэффициент.
Пример 1. Превратим неприведенное уравнение: 8x 2 + 20x — 9 = 0 — в приведенное.
Для этого разделим обе части исходного уравнения на старший коэффициент 8:
Ответ: равносильное данному приведенное уравнение x 2 + 2,5x — 1,125 = 0.
Полные и неполные квадратные уравнения
В определении квадратного уравнения есть условие: a ≠ 0. Оно нужно, чтобы уравнение ax 2 + bx + c = 0 было именно квадратным. Если a = 0, то уравнение обретет вид линейного: bx + c = 0.
Что касается коэффициентов b и c, то они могут быть равны нулю, как по отдельности, так и вместе. В таком случае квадратное уравнение принято назвать неполным.
Неполное квадратное уравнение —— это квадратное уравнение вида ax 2 + bx + c = 0, где оба или хотя бы один из коэффициентов b и c равен нулю.
Полное квадратное уравнение — это уравнение, у которого все коэффициенты отличны от нуля.
Такие уравнения отличны от полного квадратного тем, что их левые части не содержат либо слагаемого с неизвестной переменной, либо свободного члена, либо и того и другого. Отсюда и их название — неполные квадратные уравнения.
Решение неполных квадратных уравнений
Как мы уже знаем, есть три вида неполных квадратных уравнений:
Давайте рассмотрим по шагам, как решать неполные квадратные уравнения по видам.
Как решить уравнение ax 2 = 0
Начнем с решения неполных квадратных уравнений, в которых b и c равны нулю, то есть, с уравнений вида ax 2 = 0.
Уравнение ax 2 = 0 равносильно x 2 = 0. Такое преобразование возможно, когда мы разделили обе части на некое число a, которое не равно нулю. Корнем уравнения x 2 = 0 является нуль, так как 0 2 = 0. Других корней у этого уравнения нет, что подтверждают свойства степеней.
Таким образом, неполное квадратное уравнение ax 2 = 0 имеет единственный корень x = 0.
Пример 1. Решить −6x 2 = 0.
Как решить уравнение ax 2 + с = 0
Обратим внимание на неполные квадратные уравнения вида ax 2 + c = 0, в которых b = 0, c ≠ 0. Мы давно знаем, что слагаемые в уравнениях носят двусторонние куртки: когда мы переносим их из одной части уравнения в другую, они надевает куртку на другую сторону — меняют знак на противоположный.
Еще мы знаем, что если обе части уравнения поделить на одно и то же число (кроме нуля) — у нас получится равносильное уравнение. Ну есть одно и то же, только с другими цифрами.
Держим все это в голове и колдуем над неполным квадратным уравнением (производим «равносильные преобразования»): ax 2 + c = 0:
Ну все, теперь мы готовы к выводам о корнях неполного квадратного уравнения. В зависимости от значений a и c, выражение — c/а может быть отрицательным или положительным. Разберем конкретные случаи.
Неполное квадратное уравнение ax 2 + c = 0 равносильно уравнению ax 2 + c = 0, которое:
Пример 1. Найти решение уравнения 8x 2 + 5 = 0.
Ответ: уравнение 8x 2 + 5 = 0 не имеет корней.
Как решить уравнение ax 2 + bx = 0
Осталось разобрать третий вид неполных квадратных уравнений, когда c = 0.
Неполное квадратное уравнение ax 2 + bx = 0 можно решить методом разложения на множители. Как разложить квадратное уравнение:
Разложим на множители многочлен, который расположен в левой части уравнения — вынесем за скобки общий множитель x.
Теперь можем перейти от исходного уравнения к равносильному x * (ax + b) = 0. А это уравнение равносильно совокупности двух уравнений x = 0 и ax + b = 0, последнее — линейное, его корень x = −b/a.
Таким образом, неполное квадратное уравнение ax 2 + bx = 0 имеет два корня:
Пример 1. Решить уравнение 0,5x 2 + 0,125x = 0
0,5x = 0,125,
х = 0,125/0,5
Ответ: х = 0 и х = 0,25.
Формула Виета
Если в школьной геометрии чаще всего используется теорема Пифагора, то в школьной алгебре ведущую роль занимают формулы Виета. Теорема звучит так:
Сумма корней x 2 + bx + c = 0 равна второму коэффициенту с противоположным знаком, а произведение корней равняется свободному члену.
Если дано x 2 + bx + c = 0, где x₁ и x₂ являются корнями, то справедливы два равенства:
Знак системы, который принято обозначать фигурной скобкой, означает, что значения x₁ и x₂ удовлетворяют обоим равенствам.
Рассмотрим теорему Виета на примере: x 2 + 4x + 3 = 0.
Пока неизвестно, какие корни имеет данное уравнение. Но в соответствии с теоремой можно записать, что сумма этих корней равна второму коэффициенту с противоположным знаком. Он равен четырем, значит будем использовать минус четыре:
Произведение корней по теореме соответствует свободному члену. В данном случае свободным членом является число три. Значит:
Необходимо проверить равна ли сумма корней −4, а произведение 3. Для этого найдем корни уравнения x 2 + 4x + 3 = 0. Воспользуемся формулами для чётного второго коэффициента:
2 + 4x + 3 = 0″ height=»215″ src=»https://lh5.googleusercontent.com/E_X403ETh_88EANRWdQN03KRT8yxP2HO4HoCrxj__c8G0DqmNJ1KDRqtLH5Z1p7DtHm-rNMDB2tEs41D7RHpEV5mojDTMMRPuIkcW33jVNDoOe0ylzXdHATLSGzW4NakMkH2zkLE» width=»393″>
Получилось, что корнями уравнения являются числа −1 и −3. Их сумма равняется второму коэффициенту с противоположным знаком, а значит решение верное.
2 + 4x + 3 = 0″ height=»52″ src=»https://lh5.googleusercontent.com/VzGPXO9B0ZYrr9v0DpJfXwuzeZtjYnDxE_ma76PUC8o7jVWwa8kZjTJhq2Lof0TiJXAp_ny3yRwI_OyRzeucv9xUZ63yoozGPP4xd4OxvElVT7Pt-d6xL5w17e_mQNs5qZJQiwfG» width=»125″>
Произведение корней −1 и −3 по теореме Виета должно равняться свободному члену, то есть числу 3. Это условие также выполняется:
2 + 4x + 3 = 0″ height=»52″ src=»https://lh4.googleusercontent.com/Cq-LCFmY3YGNSan1VF3l3CqIeojoJYAvGAiTBWnzyoZu_xJFrF5NfQ3xCe59apJklw6uYbmQ4lAkBTeC-TJmEGicN3rgGtsezhuqdNiOWjZT39NziOB5uOmQr3cr9-5fNnepdZDo» width=»112″>
Результат проделанных вычислений в том, что мы убедились в справедливости выражения:
Когда дана сумма и произведение корней квадратного уравнения, принято начинать подбор подходящих корней. Теорема, обратная теореме Виета, при таких условиях может быть главным помощником. Вот она:
Обратная теорема Виета
Если числа x1 и x2 таковы, что их сумма равна второму коэффициенту уравнения x 2 + bx + c = 0, взятому с противоположным знаком, а их произведение равно свободному члену, то эти числа и есть корни x 2 + bx + c = 0.
Обычно вся суть обратных теорем в том самом выводе, которое дает первая теорема. Так, при доказательстве теоремы Виета стало понятно, что сумма x1 и x2 равна −b, а их произведение равно c. В обратной теореме это и есть утверждение.
Пример 1. Решить при помощи теоремы Пифагора: x 2 − 6x + 8 = 0.
2 − 6x + 8 = 0″ height=»59″ src=»https://user84060.clients-cdnnow.ru/uploads/5fc101ce2e346034751939.png» width=»117″>
Чтобы проще подобрать корни, нужно их перемножить. Число 8 можно получить путем перемножения чисел 4 и 2 либо 1 и 8. Но значения x1 и x2 надо подбирать так, чтобы они удовлетворяли и второму равенству тоже.
Можно сделать вывод, что значения 1 и 8 не подходят, так как они не удовлетворяют равенству x1 + x2 = 6. А значения 4 и 2 подходят обоим равенствам:
Как разложить квадратное уравнение
С помощью теоремы Виета можно получить формулу разложения квадратного трехчлена на множители. Выглядит она так:
Формула разложения квадратного трехчлена
Если x1 и x2 — корни квадратного трехчлена ax 2 + bx + c, то справедливо равенство ax 2 + bx + c = a (x − x1) (x − x2).
Дискриминант: формула корней квадратного уравнения
Чтобы найти результат квадратного уравнения, придумали формулу корней. Выглядит она так:
где D = b 2 − 4ac — дискриминант квадратного уравнения.
Эта запись означает:
Чтобы легко применять эту формулу, нужно понять, как она получилась. Давайте разбираться.
Выводим формулу корней квадратного уравнения
Продолжим изучать формулу корней квадратного уравнения.
Пусть перед нами есть задача решить квадратное уравнение ax 2 + bx + c = 0. Выполним ряд равносильных преобразований:

после чего уравнение примет вид
Так, мы пришли к уравнению 
Отсюда выводы про корни уравнения 
И еще один вывод: есть у уравнения корень или нет, зависит от знака выражения в правой части. При этом важно помнить, что знак этого выражения задается знаком числителя. Потому выражение принято называть дискриминантом квадратного уравнения и обозначается буквой D.
По значению и знаку дискриминанта можно сделать вывод, есть ли действительные корни у квадратного уравнения, и сколько.
Алгоритм решения квадратных уравнений по формулам корней
Теперь мы знаем, что при решении квадратных уравнения можно использовать универсальную формулу корней — это помогает находить комплексные корни.
В 8 классе на алгебре можно встретить задачу по поиску действительных корней квадратного уравнения. Для этого важно перед использованием формул найти дискриминант и убедиться, что он неотрицательный, и только после этого вычислять значения корней. Если дискриминант отрицательный, значит уравнение не имеет действительных корней.
Алгоритм решения квадратного уравнения ax 2 + bx + c = 0:
Чтобы запомнить алгоритм решения квадратных уравнений и с легкостью его использовать, давайте тренироваться!
Примеры решения квадратных уравнений
Как решать квадратные уравнения мы уже знаем, осталось закрепить знания на практике.
Пример 1. Решить уравнение −4x 2 + 28x — 49 = 0.
Ответ: единственный корень 3,5.
Пример 2. Решить уравнение 54 — 6x 2 = 0.
Ответ: два корня 3 и — 3.
Пример 3. Решить уравнение x 2 — х = 0.
Ответ: два корня 0 и 1.
Пример 4. Решить уравнение x 2 — 10 = 39.
Ответ: два корня 7 и −7.
Пример 5. Решить уравнение 3x 2 — 4x+94 = 0.
D = (-4) 2 — 4 * 3 * 94 = 16 — 1128 = −1112
В школьной программе за 8 класс нет обязательного требования искать комплексные корни, но такой подход может ускорить ход решения. Если дискриминант отрицательный — сразу пишем ответ, что действительных корней нет и не мучаемся.
Формула корней для четных вторых коэффициентов
Рассмотрим частный случай. Формула решения корней квадратного уравнения 
2 + 2nx + c = 0″ height=»705″ src=»https://user84060.clients-cdnnow.ru/uploads/5fc11a460e2f8354381151.png» width=»588″>
Самые внимательные уже заметили, что D = 4D1, или D1= D/4. Проще говоря, D1 — это четверть дискриминанта. И получается, что знак D1 является индикатором наличия или отсутствия корней квадратного уравнения.
Сформулируем правило. Чтобы найти решение квадратного уравнения со вторым коэффициентом 2n, нужно:
Упрощаем вид квадратных уравнений
Если мы ходили в школу всегда одной тропинкой, а потом вдруг обнаружили путь короче — это значит теперь у нас есть выбор: упростить себе задачу и сократить время на дорогу или прогуляться по привычному маршруту.
Так же и при вычислении корней квадратного уравнения. Ведь проще посчитать уравнение 11x 2 — 4 x — 6 = 0, чем 1100x 2 — 400x — 600 = 0.
Часто упрощение вида квадратного уравнения можно получить через умножение или деление обеих частей на некоторое число. Например, в предыдущем абзаце мы упростили уравнение 1100x 2 — 400x — 600 = 0, просто разделив обе части на 100.
Такое преобразование возможно, когда коэффициенты не являются взаимно простыми числами. Тогда принято делить обе части уравнения на наибольший общий делитель абсолютных величин его коэффициентов.
А умножение обеих частей квадратного уравнения отлично помогает избавиться от дробных коэффициентов. Умножать в данном случае лучше на наименьшее общее кратное знаменателей его коэффициентов. Например, если обе части квадратного уравнения
умножить на НОК (6, 3, 1) = 6, то оно примет более простой вид x 2 + 4x — 18 = 0.
Связь между корнями и коэффициентами
Мы уже запомнили, что формула корней квадратного уравнения выражает корни уравнения через его коэффициенты:
Из этой формулы, можно получить другие зависимости между корнями и коэффициентами.
Например, можно применить формулы из теоремы Виета:
Можно активно использовать уже записанные формулы и с их помощью получить ряд других связей между корнями и коэффициентами квадратного уравнения. Таким образом можно выразить сумму квадратов корней квадратного уравнения через его коэффициенты:
А еще найти корни квадратного уравнения можно с помощью онлайн-калькулятора. Пользуйтесь им, если уже разобрались с темой и щелкаете задачки легко и без помощников:
Бесплатный марафон: как самому создавать игры, а не только играть в них (◕ᴗ◕)
Записаться на марафон
Бесплатный марафон: как самому создавать игры, а не только играть в них (◕ᴗ◕)