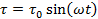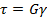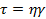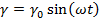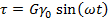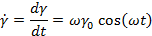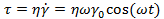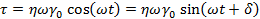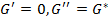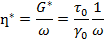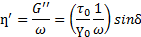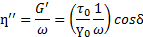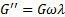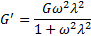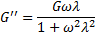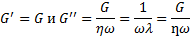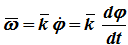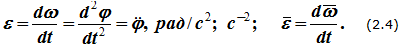чем больше угловая скорость тем комплексный модуль g
Тема 10. Испытания в режиме вынужденных колебаний
Большую популярность приобрел метод, который заключается в том, что вместо приложения к образцу постоянного напряжения и измерения реологических характеристик в режиме установившегося течения образец подвергают осциллирующим напряжениям или деформациям. В реометрах, в режиме CS, приложенное напряжение может быть описано синусоидальной функцией времени:
При динамических испытаниях получают данные о вязкой и упругой реакциях образца в зависимости от скорости воздействия на него, иными словами, получают зависимость осциллирующего напряжения или деформации от заданной угловой скорости или частоты. Поскольку обычные измерения проводят не толькопри одной заданной частоте, а в широком диапазоне частот, они занимают довольно много времени.
В то время как измерение динамической вязкости ньютоновской жидкости в режиме установившегося ротационного течения (после достижения заданного уровня температуры) занимает одну или две минуты, измерение вязкоупругости полимера может занять в десять раз больше времени как в режиме динамических испытаний, так и при испытаниях ползучести и восстановления.
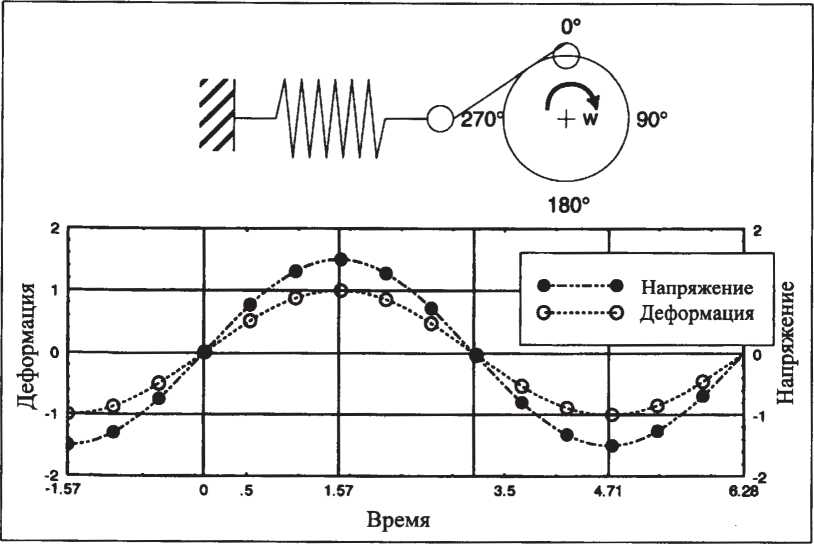
Следует иметь в виду, что при работе в области линейной вязкоупругости динамические испытания могут быть проведены как на CS-, так и на CR-реометрах с идентичными результатами. Проведение динамических испытаний на ротационном вискозиметре означает, что ротор, верхняя плита или конус больше не вращаются с постоянной скоростью в одном направлении, а попеременно отклоняются по синусоидальной временной функции* на малый угол ф вправо и влево. Это вызывает аналогичную синусоидальную деформацию образца, помещенного в измерительный зазор, и соответствующую синусоидальную картину изменения напряжений, амплитуда которых связана с природой испытуемого образца.
Чтобы не выйти за пределы области линейной вязкоупругости, угол отклонения ротора почти всегда очень мал, часто не более 1° (рис. 36).
 Угловая скорость (1/с) Рис. 36. Динамические испытания: задание осциллирующих деформаций или напряжений Угловая скорость (1/с) Рис. 36. Динамические испытания: задание осциллирующих деформаций или напряжений |
Из этого следует очень важный вывод, касающийся динамических испытаний и сферы их применения: в процессе динамических испытаний вязкоупругих жидкостей и даже твердых тел не только не происходит механического разрушения образцов, но и сохраняется их внутренняя структура. С реологической точки зрения структура испытуемых образцов находится как бы в “состоянии покоя”.
Некоторые теоретические аспекты динамических испытаний
Чтобы создать некую основу для интерпретации результатов динамических испытаний, проведем теоретическое обсуждение, используя модели спираль-демпфер (теоретически менее подготовленными читателями оно может быть опущено).
Как уже было показано, спираль моделирует упругую реакцию образца, определяемую как
Демпферы моделируют реакцию ньютоновской жидкости, которая определяется следующим образом:
Упомянутые основные реологические элементы – как сами по себе, так и их различные сочетания – обсуждаются на этот раз с точки зрения динамических испытаний.
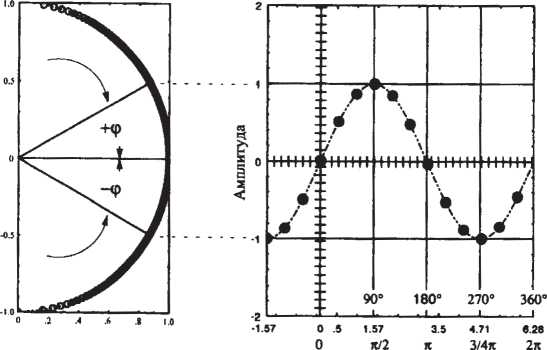
Модель спирали (рис. 37). Этот рисунок показывает, как спираль может подвергаться осциллирующей деформации, когда конец кривошипа, закрепленный на коленчатом валу, поворачивается на один полный оборот, а второй конец сжимает и растягивает пружину. Если угловая скорость равна со, а максимальная деформация пружины γ0, то изменение деформации в функции времени можно записать как
а зависимость напряжения в функции времени будет иметь вид
Эти зависимости в графическом виде представлены на рис. 37, откуда видно, что в случае этой модели деформация и напряжение совпадают по фазе: при максимальной деформации и результирующее напряжение также максимально.
Модель демпфера(рис. 38). Если заменить спираль на демпфер и двигать поршень с помощью аналогичного кривошипа, можно получить следующее уравнение:
Подставляя это выражение в уравнение демпфера, получим
Рис. 37. Динамическое испытание: измерение напряжения в зависимости от заданной деформации для упругого твердого тела (пружины).
Рис. 38. Динамическое испытание: измерение напряжения в зависимости от заданной деформации для ньютоновской жидкости (демпфера).
Из рис. 38 очевидно, что напряжение (реакция демпфера на сдвиг) отстает от деформации на 90°. Это отставание также может быть выражено через угол сдвига фаз δ = 90°, на который заданная деформация опережает измеренное напряжение.
Уравнение может быть переписано следующим образом:
Всякий раз, когда деформация демпфера достигает максимума, скорость изменения деформации становится равной нулю (у = 0); когда же величина деформации, проходя через ноль, меняет знак с положительного на отрицательный, скорость ее изменения самая высокая, что приводит к максимальной величине напряжения.
Полученные на этом этапе результаты необходимо преобразовать в вязкую и упругую компоненты вязкоупругого поведения образца. Это лучше всего сделать посредством метода численного сглаживания Гаусса, часто используемого в математике и физике.
Рис. 42. Динамическое испытание: развертка по угловой скорости.
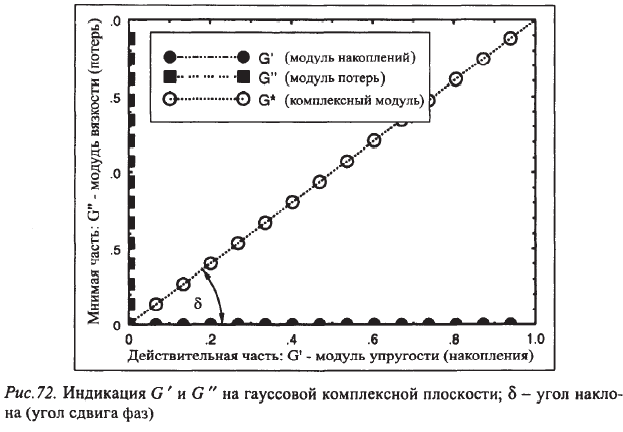
Применение метода численного сглаживания Гаусса для разделения вязкого и упругого поведения образцов, подвергнутых динамическим испытаниям(рис. 43). В этом методе пользуются комплексными числами, которые позволяют работать с корнем из отрицательного числа
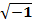
и комплексные числа могут быть представлены как векторы с действительными и мнимыми осями (компонентами).
Комплексный модуль G * может быть определен следующим образом:
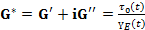
Рис.43. Индикация модулей накопления и потерь на гауссовой комплексной плоскости.
В этом уравнении величины G’ и G»обозначают:
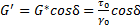
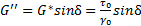
Термин “модуль накопления” указывает на то, что энергия напряжения была временно запасена в процессе испытания, но она может быть впоследствии возвращена. Термин “модуль потерь” говорит о том, что энергия, использованная для инициирования течения, необратимо перешла в теплоту (“потеряна”).
Если вещество чисто вязкое, то угол сдвига фаз 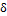
Если вещество чисто упругое, то угол сдвига фаз 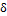
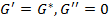
Из комплексного модуля G* можно определить комплексную вязкость η|*:
Комплексная вязкость отражает общее сопротивление динамическому сдвигу. Ее также можно разложить на две компоненты – запасенную (мнимую) вязкость 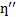
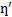
Зависимость динамических данных от угловой скорости. Реальные вещества не являются ни телами Кельвина-Фойхта, ни максвелловскими жидкостями, а представляют собой сложную комбинацию этих основных моделей. Чтобы оценить динамические характеристики реальных веществ, полезно рассмотреть поведение этих двух основных моделей при изменении угловой скорости.
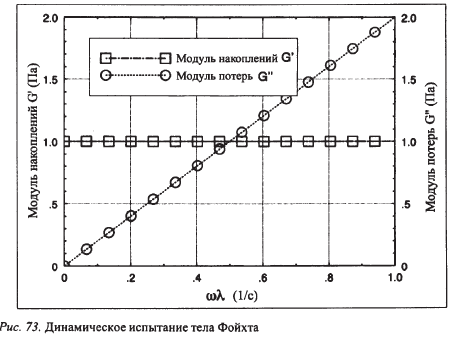
При динамическом испытании тела Фойхта модули выражаются следующим образом: G’ прямо связан с модулем пружины G, тогда как
Из этого следует, что G’ не зависит от частоты, тогда как G»линейно связан с частотой. При низких частотах поведение этого модельного вещества определяется поведением его пружины, т.е. упругая компонента G’ превышает вязкую компоненту G». При промежуточной частоте величины обеих компонент равны, а при высоких частотах вязкая компонента становится преобладающей.
Используя равенство 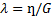
При динамическом испытании жидкости Максвелла модули в функции 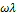
Когда член 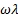
(вязкость демпфера/модуль пружины), тогда
Когда член 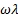
При низких частотах вязкая компонента G» выше, чем упругая 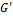
Рис. 44. Динамические испытания тела Фойхта.
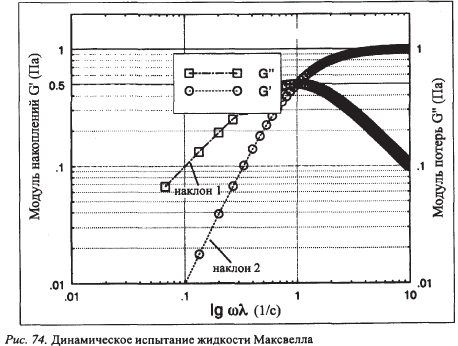
При оценке результатов динамических испытаний представляют интерес частота, при которой пересекаются кривые обоих модулей, и наклон частотных зависимостей, особенно при низких частотах.
Для очень низких значений угловой скорости по величине G» можно оценить динамическую вязкость демпфера ƞ= G»/ 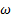
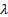
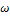
Рис. 45. Динамические испытания жидкости Максвелла
Соотношение Кокса—Мерца. Два ученых, которые дали этому соотношению свое имя, эмпирически установили, что вязкость при стационарном сдвиге, измеренная в зависимости от скорости сдвига, может быть непосредственно связана с динамической комплексной вязкостью ƞ*, измеренной как функция угловой скорости:
ƞ( 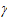
Было обнаружено, что это соотношение справедливо для многих расплавов и растворов полимеров, но редко дает приемлемые результаты для суспензий.
Преимущество соотношения Кокса-Мерца состоит в том, что технически проще работать с частотой, чем со скоростями сдвига. На ротационных вискозиметрах невозможно проводить испытания расплавов и растворов полимеров при высоких скоростях сдвига из-за проявления эластичности – эффекта Вайссенберга. Поэтому вместо измерений кривой течения при стационарном сдвиге проще провести динамические испытания и использовать комплексную вязкость.
Определение области линейной вязкоупругости. В разделе, описывающем испытания ползучести и восстановления, было показано, насколько важно проводить измерения в области линейной вязкоупругости. Эта область имеет также большое значение и при динамических испытаниях. Чтобы определить границу между линейной и нелинейной областями вязкоупругости, проведем одно простое исследование.
На схематической диаграмме (рис. 48) кривая комплексного модуля сначала проходит параллельно оси абсцисс (в данном примере
lgG* = 0,5 и на этом участке не зависит от амплитуды), а при lg 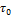
Рис. 48. Динамическое испытание: развертка по амплитуде напряжения.
Область линейной вязкоупругости ограничена таким интервалом амплитуд, в котором значение G*постоянно. В теории линейной вязкоупругости соответствующие уравнения являются линейными дифференциальными уравнениями и коэффициенты дифференциалов по времени являются постоянными, т.е. материальными константами. Выход за пределы области линейной вязкоупругости при использовании более высоких амплитуд и, следовательно, повышенных напряжений означает появление неучитываемых отклонений результатов измерений, связанных с выбором параметров испытаний и применяемой аппаратуры. При таких условиях образец деформируется до момента, когда физические связи между молекулами или агрегатами разрушаются, наступает сдвиговое разжижение, и большая часть вводимой энергии необратимо переходит в теплоту.
Нужно отметить следующее. Так как чрезвычайно важно определить область линейной вязкоупругости, любые динамические испытания неизвестных образцов необходимо начинать с развертки по амплитуде напряжения.
iSopromat.ru
Рассмотрим понятия угловой скорости и углового ускорения при вращении твердого тела:
Угловая скорость
Угловой скоростью называют скорость вращения тела, определяющаяся приращением угла поворота тела за промежуток времени.
Обозначение: ω (омега).
Формулы угловой скорости
Формула для расчета угловой скорости в зависимости от заданных параметров вращения может иметь вид:
Быстрота изменения угла φ (перемещения из положения П1 в положение П2) – это и есть угловая скорость:
Например, тело совершающее 1,5 оборота за одну секунду имеет угловую скорость
Приняв k как единичный орт положительного направления оси, получим:
Вектор угловой скорости – скользящий вектор: он может быть приложен к любой точке оси вращения и всегда направлен вдоль оси, при положительном значении угловой скорости направления ω и k совпадают, при отрицательном – противоположны.
Угловое ускорение
Угловое ускорение характеризует величину изменения угловой скорости при вращении твердого тела:
Вектор углового ускорения так же направлен по оси вращения. При ускоренном вращении их направления совпадают, при замедленном — противоположны.
Другими словами, при положительном ускорении угловая скорость нарастает, а при отрицательном вращение замедляется.
Для некоторых частных случаев вращательного движения твердого тела могут быть использованы формулы:
В технике угловая скорость часто задается в оборотах в минуту n [об/мин]. Один оборот – это 2π радиан:
Уважаемые студенты!
На нашем сайте можно получить помощь по техническим и другим предметам:
✔ Решение задач и контрольных
✔ Выполнение учебных работ
✔ Помощь на экзаменах
Угловая скорость.
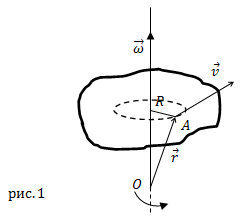
Угловой скоростью называется величина, численно равная скорости точек, расположенных от оси на расстоянии единицы длины.
При вращении тела вокруг неподвижной оси АВ каждая точка тела М описывает окружность, перпендикулярную к оси, центр Р которой лежит на оси.
Скорость точки M направлена нормально к плоскости МАВ в сторону вращения. Равномерное вращение точки характеризуется постоянной угловой скоростью.
Угловой скоростью тела называют отношение угла поворота к интервалу времени, в течение которого совершен этот поворот. Если угловую скорость обозначить через w, то:
Угловая скорость выражается в радианах в секунду (рад/с).
При равномерном вращении, когда известна угловая скорость в начальный момент времени t0 = 0, можно определить угол поворота тела за время t и тем самым положение точек тела:
За один период (промежуток времени Т, в течение которого тело совершает один оборот по окружности) угол поворота φ равен 2π рад: 2π = wT, откуда:
Связь угловой скорости с периодом Т и частотой вращения ν выражается соотношением:
А связь между линейной и угловой скоростями определяется соотношением:
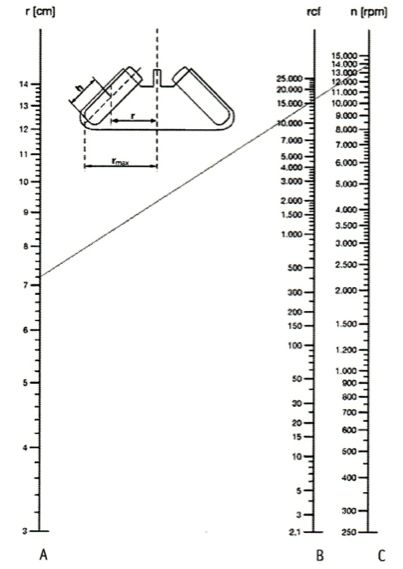
Центрифугирование: как определить ускорение (число g) в зависимости от скорости вращения и диаметра ротора
Центрифугирование – способ разделения неоднородных, дисперсных жидких систем на фракции по плотности под действием центробежных сил. Центрифугирование осуществляют в центрифугах, принцип работы которых основан на создании центробежной силы, увеличивающей скорость разделения компонентов смеси по сравнению со скоростью их разделения только под влиянием силы тяжести. Разделение веществ с помощью центрифугирования основано на разном поведении частиц в центробежном поле. В центробежном поле частицы, имеющие разную плотность, форму или размеры, осаждаются с разной скоростью.
Центробежное ускорение тогда будет равно: g =p 2 x r x n 2 /900.
Относительное ускорение центрифуги (rcf) задается, как кратное от ускорения свободного падения (g). Оно является безразмерной величиной и служит для сравнения производительности разделения и осаждения. Относительное ускорение центрифуги (rcf) зависит от частоты вращения и радиуса центрифугирования.
Существует номограмма, выражающая зависимость относительного ускорения центрифуги (rcf) от скорости вращения ротора (n) и радиуса (r) – среднего радиуса вращения столбика жидкости в центрифужной пробирке (т.е. расстояния от оси вращения до середины столбика жидкости). Радиус измеряется (см) от оси вращения ротора до середины столбика жидкости в пробирке, когда держатель находится в положении центрифугирования.
Номограмма для определения относительного ускорения центрифуги (rcf) в зависимости от скорости вращения и диаметра ротора
r – радиус ротора, см
n – скорость вращения ротора, оборотов в минуту
rcf (relative centrifuge force) – относительное ускорение центрифуги
Радиус центрифугирования rmax– это расстояние от оси вращения ротора до дна гнезда ротора.
Для определения ускорения с помощью линейки совмещаем значения радиуса и числа оборотов на и на шкале rcf определяем его величину.
Пример: на шкале А отмечаем значение rрадиуса для ротора – 7,2 см, на шкале С отмечаем значение скорости ротора –14,000 об/мин, соединяем эти две точки. Точка пересечения образованного отрезка со шкалой В показывает значение ускорения для данного ротора. В данном случае ускорение равно 15’000.
Формула угловой скорости
Определение и формула угловой скорости
Круговым движением точки вокруг некоторой оси называют движение, при котором траекторией точки является окружность с центром, который лежит на оси вращения, при этом плоскость окружности перпендикулярна этой оси.
Вращением тела вокруг оси называют движение, при котором все точки тела совершают круговые движения около этой оси.
Вектор угловой скорости может претерпевать изменения как за счет изменения скорости вращения тела вокруг оси (изменение модуля угловой скорости), так и за счет поворота оси вращения в пространстве ($\bar<\omega>$ при этом изменяет направление).
Равномерное вращение
Если тело за равные промежутки времени поворачивается на один и тот же угол, то такое вращение называют равномерным. При этом модуль угловой скорости находят как:
Равномерное вращение часто характеризуют при помощи периода обращения (T), который является временем, за которое тело производит один оборот ($\Delta \varphi=2 \pi$). Угловая скорость связана с периодом обращения как:
С числом оборотов в единицу времени ($\nu) угловая скорость связана формулой:
Понятия периода обращения и числа оборотов в единицу времени иногда используют и для описания неравномерного вращения, но понимают при этом под мгновенным значением T, время за которое тело делало бы один оборот, если бы оно вращалось равномерно с данной мгновенной величиной скорости.
Формула, связывающая линейную и угловую скорости
Единицы измерения угловой скорости
Основной единицей измерения угловой скорости в системе СИ является: [$\omega$]=рад/с
Примеры решения задач
Решение. Для нахождения модуля угловой скорости применим формулу:
Вычислим, чему будет равна угловая скорость в заданный момент времени (при t=0,5 c):
Ответ. В заданный момент времени тело имеет угловую скорость равную нулю, следовательно, она останавливается.
Формула угловой скорости не по зубам? Тебе ответит эксперт через 10 минут!
Задание. Скорости вращения тела заданы системой уравнений:
Модуль угловой скорости связан с углом поворота как:
Следовательно, угол поворота найдем как: