какую функцию называют непрерывной на промежутке
Непрерывность функции на промежутке



Определение. Функция называется непрерывной на интервале, если она непрерывна в каждой точке этого интервала.
Если функция определена при х = а и при этом 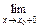
то говорят, что f(х) в точке а непрерывна справа. Аналогично, если 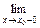
Определение. Функция называется непрерывной на отрезке [a, b], если она непрерывна в каждой его точке (в точке а непрерывна справа, в точке b – непрерывна слева).
Функции, непрерывные на отрезке, обладают рядом важных свойств, которые выражаются следующими теоремами.
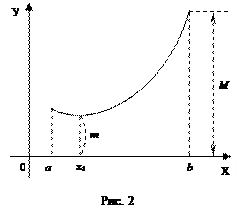
Теорема 3.3.1. Функция, непрерывная на отрезке [a, b], достигает на нём своего наименьшего значения m и наибольшего значения M, то есть существуют такие точки x1 и x2 этого отрезка, что f(x1) = m, f(x2) = M.
Теорема имеет простой геометрический смысл (см. рис.2).
 |
Теорема 3.3.2. Если функция у = f(x) непрерывна на отрезке [a, b] и на его концах принимает неравные значения f(а) = А, f(b) = В, А ¹ В, то каково бы ни было число С, заключённое между А и В, найдётся точка с Î [a, b] такая, что f(с) = С.
Геометрический смысл теоремы иллюстрируется на рис.3. Всякая прямая у = С, где A C > B), пересекает график функции у = f(x).
Следствие. Если функция непрерывна на отрезке и на его концах принимает значения разных знаков, то на этом отрезке найдётся хотя бы одна точка, в которой функция обращается в нуль.
Геометрический смысл следствия иллюстрируется на рис.4.
Вопросы для самоконтроля
1. Какая функция называется непрерывной в точке?
2. Приведите еще одно эквивалентное определение через приращение функции и аргументов.
3. Что можно сказать о сумме, разности, произведении и частном двух непрерывных функций?
4. При каких значениях аргумента целая рациональная и дробно-рациональная функции непрерывны?
5. Когда сложная функция непрерывна в точке?
6. Что называется точкой разрыва функций?
7. Какие точки называются точками разрыва первого рода?
8. Какая величина называется скачком функции?
9. Разъясните понятия »точка устранимого разрыва». Приведите примеры.
10. Какие точки называются точками разрыва второго рода? Приведите примеры.
11. Разъясните понятия: »непрерывность на интервале», »непрерывность справа», »непрерывность слева», »непрерывность на отрезке».
12. Дайте определение наибольшего и наименьшего значения функций.
13. Сформулируйте теорему о связи непрерывности на отрезке с наибольшим и наименьшим значениями функции. Разъясните ее на рисунке.
14. Сформулируйте теорему о связи непрерывности функций на отрезке с отрезком значений функций. Проиллюстрируйте ее геометрический смысл на рисунке.
15. Приведите следствие из вышеуказанной теоремы и его геометрическую интерпретацию.
Тема лекции: Производная функции
План лекции: Понятие производной, её геометрический и физический смысл. Основные правила дифференцирования. Производная сложной функции. Некоторые приложения производной.
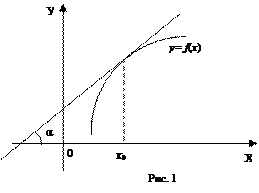
4.1. Понятие производной, её геометрический и физический смысл
Рассмотрим функцию у = f(x), заданную в интервале ]a, b[. Пусть х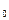
Определение. Производной функции у = f(x) в точке х0 называется предел отношения приращения этой функции к приращению аргумента, когда последнее стремится к нулю:
f’(x0) = 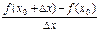
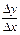
Геометрический смысл производной: производная от данной функции в точке равна тангенсу угла между осью Ох и касательной к графику этой функции в соответствующей точке (см. рис.1):
 |
Физический смысл производной: производная от пути по времени равна скорости прямолинейного движения точки: х’(t0) = v.
Функция, имеющая производную в данной точке, называется дифференцируемой в данной точке. Функция, имеющая производную в каждой точке данного промежутка, называется дифференцируемой в
этом промежутке. Операция нахождения производной называется дифференцированием.
Зависимость между непрерывностью и дифференцируемостью функции выражается следующей теоремой.
Теорема 4.1.1. Если функция у = f(x) дифференцируема в данной точке, то она непрерывна в ней.
Доказательство. Пусть функция у = f(x) дифференцируема в точке х0, то есть существует предел y’(х0) =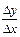
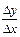

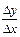


Какую функцию называют непрерывной на промежутке
Пусть функция `y=f(x)` определена на некотором интервале, содержащем точку `ain R`, за исключением, быть может, самой точки `a`.
Число `A` называется пределом функции `y=f(x)` в точке `a`, если для любой последовательности `(x_n)` из области её определения такой, что `x_n!=a` и `lim_(n->oo)x_n=a` выполняется равенство `lim_(n->oo)f(x_n)=A`.
Обозначение: `lim_(n->oo)f(x)=A`, или `f(x)->A` при `x->a`.
В определении предела рассматриваются значения `x_n`, не равные `a`, поэтому в самой точке `a` функция `y=f(x)` может быть не определена; если значение `f(a)` определено, то оно не обязано совпадать с `A`. К тому же, поскольку последовательность `(f(x_n))` имеет не более одного предела, получаем, что если функция `y=f(x)` имеет предел при `x->a`, то этот предел единственный.
На рис. 2 изображена лишь одна последовательность `(x_n)`, которая к тому же является монотонной. Важно понимать, что `lim_(n->oo)f(x_n)=A` для любой последовательности `(x_n)` с условием `x_n!=a` и `lim_(n->oo)x_n=a`.
Доказать, что `lim_(n->oo)x=a`.
Очевидно, функция `f(x)=x` определена на любом интервале, содержащем `a`. Выберем произвольную последовательность `(x_n)` такую, что `x_n!=a` и `lim_(n->oo)x_n=a`. Тогда `f(x_n)=x_n` и, значит, `lim_(n->oo)f(x_n)=a`.
Доказать, что при `a>0lim_(n->a)sqrtx=sqrta`.
Функция `f(x)=sqrtx` определена при `x>=0` и, следовательно, определена на некотором интервале, содержащем `a`. Выберем произвольную последовательность неотрицательных чисел `x_n!=a`, что `lim_(n->oo)x_n=a`. Нам нужно показать, что `lim_(n->oo)sqrtx_n=sqrta`. Фиксируем произвольное `epsilon>0`, тогда найдётся такое число `k`, что при `n>k` выполняется неравенство `|x_n-a| 1)(x^2-1)/(x-1)=2`.
Функция `f(x)=(x^2-1)/(x-1)` определена на любом интервале, содержащем `x=1`, кроме этой точки. Поскольку при `x!=1` имеет место равенство `f(x)=x+1`, то для любой последовательности `(x_n)` такой, что `x_n!=1` и `lim_(n->oo)x_n=1` выполняется `lim_(n->oo)f(x_n)=lim_(n->oo)x_n+1=2`.
Пусть функции `y=f(x)`, `y=g(x)` определены на некотором интервале, содержащем точку `a in R`, за исключением, быть может, самой точки `a`, `lim_(x->a)f(x)=A` и `lim_(x->a)g(x)=B`. Тогда
3) если дополнительно `g(x)!=0` при `x!=a`, `B!=0`, то `lim_(x->a)(f(x))/(g(x))=A/B`.
Эти свойства вытекают из арифметических операций над пределами последовательностей (теорема 2.2). Приведём доказательство для свойства 2. Остальные доказываются аналогично.
Пусть некоторая произвольная последовательность `(x_n)` из интервала, на котором определены функции, такова что `x_n!=a` и `lim_(n->oo)x_n=a`. Тогда по определению предела функции `lim_(n->oo)f(x_n)=A` и `lim_(n->oo)g(x_n)=B`. По пункту 2 теоремы 2.2 `lim_(n->oo)f(x_n)g(x_n)=AB`. По определению предела функции получаем, что `lim_(x->a)f(x)g(x)=AB`.
Пусть функция `y=f(x)` определена на некотором интервале, содержащем точку `a`. Функция `y=f(x)`называется непрерывной в точке `a`, если `lim_(x->a)f(x)=f(a)`, т. е. если для любой последовательности `(x_n)` из области определения функции такой, что `lim_(n->oo)x_n=a`, выполняется равенство `lim_(n->oo)f(x_n)=f(a)`.
Отметим два обстоятельства, связанных с определением непрерывности. Во-первых, оговорка `x_n!=a` здесь не нужна, т. к. при `x_n=a` значения `f(x_n)` равны `f(a)`. Во-вторых, важно понимать, что если функция `y=f(x)` непрерывна в точке `a`, то
1) она определена в точке `a`;
2) существует `lim_(x->a)f(x)=A` и
Если хотя бы один из пунктов 1) – 3) не выполнен, то функция не является непрерывной в точке `a`.
Многочлен является непрерывной на всей числовой прямой функцией.
Из теоремы 3.1 вытекает, что если функции `y=f(x)`, `y=g(x)` непрерывны в точке `a`, то функции `y=f(x)+-g(x)`, `y=f(x)g(x)`, `y=f(x)//g(x)` `(g(a)!=0)` также непрерывны в `a`.
Функция называется непрерывной на множестве, если она непрерывна в каждой точке этого множества.
Функция `y=|x|` непрерывна на всей числовой прямой.
Вообще, все элементарные функции, изучаемые в школьном курсе, непрерывны в каждой точке, в окрестности которой эти функции определены.
Непрерывность функции и точки разрыва
п.1. Приращение аргумента и приращение функции
 | Пусть \(y=3x-1\) \(x_0=1,\ x=1,1 \) |
п.2. Непрерывность функции в точке и на промежутке
На «языке ε-δ» определение непрерывности будет следующим:
ε-δ определение непрерывности похоже на ε-δ определение предела функции, с той разницей, что модуль \(|x-x_0|\) может быть равен 0 для непрерывной функции, т.е. сама точка \(x_0\) входит в δ-окрестность.
Все три представленных определения непрерывности функции в точке эквивалентны.
Существуют и другие эквивалентные определения. Мы дадим ещё одно из них дальше, в этом же параграфе.
п.3. Непрерывность функции на промежутке
Промежуток – это интервал, отрезок, луч и т.п. (см. §16 справочника для 8 класса).
График непрерывной функции – это непрерывная линия.
Кроме непрерывности, эта линия еще и «плавная», без «заломов».
При наличии заломов функция называется кусочно-непрерывной.
 Непрерывная функция |
 Кусочно-непрерывная функция |
п.4. Односторонние пределы
Рассмотрим гиперболу \(y=\frac<1>
Теперь рассмотрим параболу \(y=x^2-2\)
Областью определения параболы является вся числовая прямая \(x\in\mathbb
Это еще одно определение непрерывности, которым удобно пользоваться на практике.
п.5. Классификация точек разрыва
| Точки разрыва | 1-го рода Односторонние пределы существуют и конечны | Устранимые Односторонние пределы равны между собой, но не равны \(f(x_0)\) |
| Неустранимые (скачок) Односторонние пределы не равны между собой | ||
| 2-го рода Хотя бы один из односторонних пределов бесконечен или не существует |
п.6. Точки разрыва первого рода
 | \(y= \begin Односторонние пределы: \begin |
п.7. Точки разрыва второго рода
В точках разрыва 2-го рода хотя бы один из односторонних пределов бесконечен или не существует.
 | \(y=e^\frac1x, x_0=0\) |
Точка \(x_0=0\) – точка разрыва второго рода.
На практике, при моделировании реальных процессов, разрывы 2-го рода в функциональных зависимостях встречаются довольно часто. Их положено заботливо анализировать и тщательно обходить, выбирая рабочие участки характеристических кривых, – чтобы «система не пошла в разнос».
п.8. Алгоритм исследования функции на непрерывность
На входе: функция \(y=f(x)\)
Шаг 1. Найти ОДЗ функции, определить точки и промежутки, не принадлежащие ОДЗ.
Шаг 2. Составить множество точек, в которое входят точки и границы промежутков, не принадлежащие ОДЗ, а также – для кусочно-непрерывных функций – точки сшивания. Полученное множество состоит из точек, подозрительных на разрыв.
Шаг 3. Исследовать каждую из точек, подозрительных на разрыв, с помощью односторонних пределов. Если разрыв обнаружен, определить тип разрыва.
На выходе: список точек разрыва и тип разрыва для каждой точки.
п.9. Примеры
Какую функцию называют непрерывной на промежутке
СВОЙСТВА ФУНКЦИЙ, НЕПРЕРЫВНЫХ НА ОТРЕЗКЕ
Рассмотрим некоторые свойства функций непрерывных на отрезке. Эти свойства приведём без доказательства.
Функцию y = f(x) называют непрерывной на отрезке [a, b], если она непрерывна во всех внутренних точках этого отрезка, а на его концах, т.е. в точках a и b, непрерывна соответственно справа и слева.
Теорема 1. Функция, непрерывная на отрезке [a, b], хотя бы в одной точке этого отрезка принимает наибольшее значение и хотя бы в одной – наименьшее.
Теорема утверждает, что если функция y = f(x) непрерывна на отрезке [a, b], то найдётся хотя бы одна точка x1 Î [a, b] такая, что значение функции f(x) в этой точке будет самым большим из всех ее значений на этом отрезке: f(x1) ≥ f(x). Аналогично найдётся такая точка x2, в которой значение функции будет самым маленьким из всех значений на отрезке: f(x1) ≤ f(x).
Ясно, что таких точек может быть и несколько, например, на рисунке показано, что функция f(x) принимает наименьшее значение в двух точках x2 и x2‘.
Замечание. Утверждение теоремы можно стать неверным, если рассмотреть значение функции на интервале (a, b). Действительно, если рассмотреть функцию y = x на (0, 2), то она непрерывна на этом интервале, но не достигает в нём ни наибольшего, ни наименьшего значений: она достигает этих значений на концах интервала, но концы не принадлежат нашей области.
Также теорема перестаёт быть верной для разрывных функций. Приведите пример.
Следствие. Если функция f(x) непрерывна на [a, b], то она ограничена на этом отрезке.
Теорема 2. Пусть функция y = f(x) непрерывна на отрезке [a, b] и на концах этого отрезка принимает значения разных знаков, тогда внутри отрезка [a, b] найдется, по крайней мере, одна точка x = C, в которой функция обращается в ноль: f(C) = 0, где a 2
а) в произвольной точке;
МЕХАНИЧЕСКИЙ СМЫСЛ ПРОИЗВОДНОЙ
Из физики известно, что закон равномерного движения имеет вид s = v·t, где s – путь, пройденный к моменту времени t, v– скорость равномерного движения.
Однако, т.к. большинство движений происходящих в природе, неравномерно, то в общем случае скорость, а, следовательно, и расстояние sбудет зависеть от времени t, т.е. будет функцией времени.
Итак, пусть материальная точка движется по прямой в одном направлении по закону s=s(t).
Отметим некоторый момент времени t0. К этому моменту точка прошла путь s=s(t0). Определим скорость vматериальной точки в момент времени t0.
Для этого рассмотрим какой-нибудь другой момент времени t0+Δt. Ему соответствует пройденный путь s=s(t0+Δt). Тогда за промежуток времени Δt точка прошла путь Δs=s(t0+Δt)–s(t).
Рассмотрим отношение 
Итак, скоростью движения в данный момент времени t0 (мгновенной скоростью) называется предел средней скорости в промежутке от t0 до t0+Δt, когда Δt→0:

т.е. скорость неравномерного движения это производная от пройденного пути по времени.
ГЕОМЕТРИЧЕСКИЙ СМЫСЛ ПРОИЗВОДНОЙ
Введем сначала определение касательной к кривой в данной точке.
Пусть имеем кривую и на ней фиксированную точку М0 (см. рисунок).Рассмотрим другую точку М этой кривой и проведем секущую M0M. Если точка М начинает перемещаться по кривой, а точка М0 остается неподвижной, то секущая меняет свое положение. Если при неограниченном приближении точки М по кривой к точке М0 с любой стороны секущая стремится занять положение определенной прямой М0Т, то прямая М0Т называется касательной к кривой в данной точке М0.
Т.о., касательной к кривой в данной точке М0 называется предельное положение секущей М0М, когда точка М стремится вдоль кривой к точке М0.
Рассмотрим теперь непрерывную функцию y=f(x) и соответствующую этой функции кривую. При некотором значении х0 функция принимает значение y0=f(x0). Этим значениям x0 и y0 на кривой соответствует точка М0(x0; y0). Дадим аргументу x0 приращение Δх. Новому значению аргумента соответствует наращенное значение функции y0+Δ y=f(x0–Δx). Получаем точку М(x0+Δx; y0+Δy). Проведем секущую М0М и обозначим через φ угол, образованный секущей с положительным направлением оси Ox. Составим отношение 

Если теперь Δx→0, то в силу непрерывности функции Δу→0, и поэтому точка М, перемещаясь по кривой, неограниченно приближается к точке М0. Тогда секущая М0М будет стремиться занять положение касательной к кривой в точке М0, а угол φ→α при Δx→0, где через α обозначили угол между касательной и положительным направлением оси Ox. Поскольку функция tg φ непрерывно зависит от φ при φ≠π/2 то при φ→α tg φ → tg α и, следовательно, угловой коэффициент касательной будет:
Т.о., геометрически у ‘(x0) представляет угловой коэффициент касательной к графику этой функции в точке x0, т.е. при данном значении аргумента x, производная равна тангенсуугла, образованного касательной к графику функции f(x) в соответствующей точке М0 (x; y) с положительным направлением оси Ox.
Пример. Найти угловой коэффициент касательной к кривой у = х 2 в точке М(-1; 1).
Ранее мы уже видели, что (x 2 )’ = 2х. Но угловой коэффициент касательной к кривой есть tg α = y‘|x=-1 = – 2.
ДИФФЕРЕНЦИРУЕМОСТЬ ФУНКЦИЙ. НЕПРЕРЫВНОСТЬ ДИФФЕРЕНЦИРУЕМОЙ ФУНКЦИИ
Функция y=f(x) называется дифференцируемой в некоторой точке x0, если она имеет в этой точке определенную производную, т.е. если предел отношения 
Если функция дифференцируема в каждой точке некоторого отрезка [а; b] или интервала (а; b), то говорят, что она дифференцируема на отрезке [а; b] или соответственно в интервале (а; b).
Справедлива следующая теорема, устанавливающая связь между дифференцируемыми и непрерывными функциями.
Теорема. Если функция y=f(x) дифференцируема в некоторой точке x0, то она в этой точке непрерывна.
Таким образом,из дифференцируемости функции следует ее непрерывность.
Доказательство. Если 

где α бесконечно малая величина, т.е. величина, стремящаяся к нулю при Δx→0. Но тогда
Таким образом, в точках разрыва функция не может иметь производной. Обратное утверждение неверно: существуют непрерывные функции, которые в некоторых точках не являются дифференцируемыми (т.е. не имеют в этих точках производной).
Рассмотрим на рисунке точки а, b, c.
В точке a при Δx→0 отношение 
В точке b при Δx→0 отношение 

В точке c односторонние производные являются бесконечно большими величинами разных знаков. В этой точке график имеет две слившиесявертикальные касательные. Тип – «точка возврата» с вертикальной касательной – частный случай угловой точки.
Покажем, что она не имеет производной в этой точке.
Т.о., отношение 
Следовательно, рассматриваемая функция не дифференцируема в точке x= 0. Касательная к кривой в этой точке образует с осью абсцисс угол p/2, т.е. совпадает с осью Oy.













