чем больше сторон имеет многоугольник тем угол между его сторонами

Многоугольник

Определение 1. Многоугольник − замкнутая ломаная линия.

Объединение многоугольника и ограниченной им части плоскости также называют многоугольником. Поэтому представим другое определение многоугольника:

Определение 2. Многоугольник − это геометрическая фигура, которая является частю плоскости, ограниченная замкнутой ломаной.

Вершины ломаной называются вершинами многоугольника. Звенья ломаной называются сторонами многоугольника.

Любой многоугольник разделяет плоскость на две части, одна из которых называется внутренней областью многоугольника, а другая внешней областью многоугольника.

Виды многоугольников

Многоугольник с тремя вершинами называется треугольником, с четыремя вершинами − четырехугольником, с пяти вершинами − пятиугольником, и т.д. Многоугольник с \( \small n \) вершинами называется \( \small n- \)угольником.

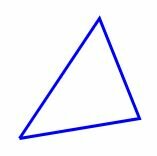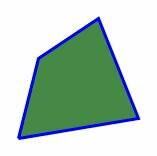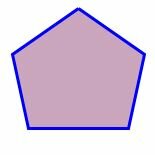На рисунке 1 представлены различные виды многоугольников.

Обозначение многоугольника

Обозначают многоугольник буквами, стоящих при его вершинах. Называют многоугольник чередовав буквы при его вершинах по часовой стрелке или против часовой стрелки. Например, многоугольник на рисунке 2 называют \( \small A_1A_2A_3A_4A_5A_6 \) или \( \small A_6A_5A_4A_3A_2A_1 \).

Соседние вершины многоугольника

Вершины многоугольника называются соседними, если они являются концами одной из его сторон.

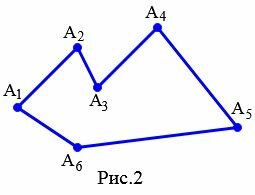На рисунке 2 вершины \( \small A_2 \) и \( \small A_3 \) являются соседними, так как они являются концами стороны \( \small A_2A_3. \)

Смежные стороны многоугольника

Стороны многоугольника называются смежными, если они имеют общую вершину.

На рисунке 2 стороны \( \small A_4A_5 \) и \( \small A_5A_6 \) являются смежными, так как они имеют общую вершину \( \small A_5. \)

Простой многоугольник. Самопересекающийся многоугольник

Многоугольник называется простым, если его несмежные стороны не имеют общих точек (внутренних или концевых).

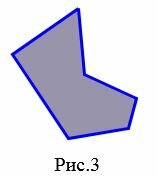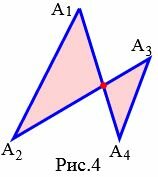На рисунке 3 изображен простой многоугольник так как стороны многоугольника не имеют самопересечений. А на рисунке 4 многоугольник не является простым, так как стороны \( \small A_1A_4 \) и \( \small A_2A_3 \) пересекаются. Такой многоугольник называется самопересекающийся многоугольник.

Выпуклый многоугольник

Многоугольник называется выпуклым, если она лежит по одну сторону от прямой, проходящей через любую его сторону.

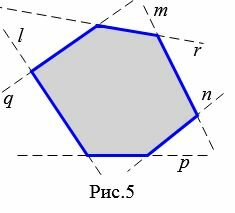На рисунке 5 многоугольник лежит по одну сторону от прямых \( \small m, \ n, \ l, \ p, \ q, \ r\) проходящих через стороны многоугольника.

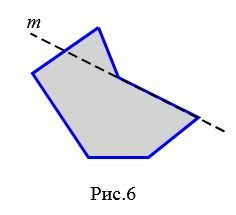На рисунке 6 прямая \( \small m\) делит многоугольник на две части, т.е. многоугольник не лежит по одну сторону от прямой \( \small m\). Следовательно многоугольник не является выпуклым.

Правильный многоугольник

Простой многоугольник называется правильным, если все его стороны равны и все углы равны. Например равносторонний треугольник является правильным многоугольником, поскольку все его стороны равны, и все его углы равны 60°. Квадрат является правильным многоугольником, так как все его стороны равны и все его углы равны 90°.

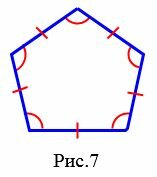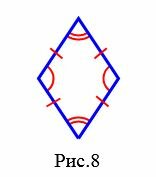На рисунке 7 изображен правильный многоугольник (пятиугольник), так как у данного многоугольника все стороны равны и все углы равны. Многоугольник (ромб) на на рисунке 8 не является правильным, так как все стороны многоугольника равны, но все углы многоугольника не равны друг другу. Прямоугольник также не является правильным многоугольником, так как несмотря на то, что все углы прямоугольника равны, но все четыре стороны прямоугольника не равны друг другу.

Звездчатый многоугольник

Самопересекающийся многоугольник, все стороны которого равны и все углы равны, называется звездчатым или звездчато-правильным.

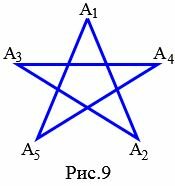На рисунке 9 представлен звездчатый пятиугольник поскольку все углы \( \small A_1, \ A_2, \ A_3, \ A_4, \ A_5 \) равны и равны все стороны: \( \small A_1A_2=A_2A_3=A_3A_4=A_4A_5=A_5A_1. \)

Периметр многоугольника

Сумма всех сторон многоугольника называется периметром многоугольника. Для многоугольника \( \small A_1A_2. A_A_n \) периметр вычисляется из формулы:

Угол многоугольника

Углом (внутренним углом) многоугольника при данной вершине называется угол между двумя сторонами многоугольника, сходящимися к этой вершине. Если многоугольник выпуклый, то все углы многоугольника меньше 180°. Если же многоугольник невыпуклый, то он имеет внутренний угол больше 180° (угол \( \small A_3 \) на рисунке 2).

Внешний угол многоугольника

Внешним углом многоугольника при данной вершине называется угол смежный внутреннему углу многоугольника при данной вершине.

На рисунке 10 угол 1 является внешним углом данного многоугольника при вершине \( \small E. \)

Диагональ многоугольника. Количество диагоналей

Диагоналями называют отрезки, соединяющие две несоседние вершины многоугольника.

Выведем форулу вычисления количества диагоналей многоугольника. Пусть задан \( \small n \)-угольник. Выберем одну вершину многоугольника и проведем мысленно все отрезки, соединяющие эту вершину с остальными вершинами. Получим \( \small n-1 \) отрезков. Но поскольку две вершины для выбранной вершины являются соседними, а по определнию диагональ − это отрезок соединяющий несоседние вершины, то из \( \small n-1 \) вычтем 2. Получим \( \small n-3 \). Всего \( \small n \) вершин. Следовательно количество вычисленных диагоналей будет \( \small n(n-3). \) Учитывая, что каждый диагональ − это отрезок соединяющий две вершины, то получится, что мы вычислили каждый диагональ дважды. Поэтому полученное число нужно делить на два. Получим количество диагоналей \( \small n- \)мерного многоугольника:

Сумма углов выпуклого многоугольника

Выведем формулу вычисления суммы углов выпуклого многоугольника. Для этого проведем из вершины \( \small A_1 \) все диагноали многоугольника \( \small A_1A_2. A_A_n \) (Рис.11):

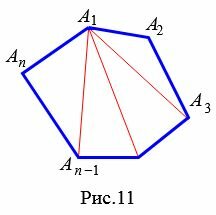Количество диагоналей, проведенной из одной вершиы, как выяснили из предыдующего параграфа равно \( \small n-3 \). Следовательно, эти диагонали разделяют многоугольник на \( \small n-3+1=n-2 \) треугольников. Поскольку сумма углов треугольника равна 180°, то получим, что сумма углов выпуклого многоугольника равна: \( \small 180°(n-2). \)

где \( \small n \) −количество сторон (вершин) выпуклого многоугольника.

Угол правильного многоугольника

Поскольку у правильного многоугольника все углы равны, то используя формулу (1) получим угол правильного многоугольника:

где \( \small n \) −количество сторон (вершин) правильного многоугольника.

Источник

Математика. 5 класс

Конспект урока

Перечень рассматриваемых вопросов:

— наглядные представления о фигурах на плоскости;

— изображение геометрических фигур.

Многоугольник – это фигура, образованная ломаной, у которой никакие два звена не имеют общих точек, кроме концов соседних звеньев ломаной.

Периметр многоугольника – это сумма всех его сторон.

Диагональ многоугольника – это отрезок, соединяющий две несмежные вершины многоугольника.

Никольский С. М. Математика. 5 класс. Учебник для общеобразовательных учреждений. // С. М. Никольский, М. К. Потапов, Н. Н. Решетников и др. – М.: Просвещение, 2017. – 272 с.

1. Чулков П. В. Математика: тематические тесты. 5 класс. // П. В. Чулков, Е. Ф. Шершнёв, О. Ф. Зарапина. – М.: Просвещение, 2009. – 142 с.

2. Шарыгин И. Ф. Задачи на смекалку: 5-6 классы. // И. Ф. Шарыгин, А. В. Шевкин. – М.: Просвещение, 2014. – 95 с.

Теоретический материал для самостоятельного изучения

Мы уже знаем, из каких элементов состоят некоторые геометрические фигуры и как их изобразить на плоскости. Сегодня мы рассмотрим многоугольник.

Ломаная линия лежит в основе построения многоугольника.

Построим ломаную. Для этого отметим на плоскости несколько точек – например, пять. Соединим их так, чтобы никакие два из отрезков, имеющих общие точки, не лежали на одной прямой. Полученная фигура и будет ломаной, которую обозначают A, B, C, D, E.

Отрезки АВ, ВС, СD,DE называются звеньями ломаной. У ломаной, которую мы изобразили, четыре звена.

Если измерить длину каждого звена и найти их сумму, то получится длина ломаной.

Измерим длину ломаной.

Сумма длин всех звеньев равна:

АВ + ВС + СD + DЕ = 14 см – длина ломаной

Теперь нарисуем ломаную таким образом, чтобы её конец совпадал с началом. Получается замкнутая ломаная A, B, C, D, E, А.

Фигуру, образованную таким образом, называют многоугольником. То есть многоугольник – это фигура, образованная ломаной, у которой никакие два звена не имеют общих точек, кроме концов соседних звеньев ломаной.

Стоит помнить, что многоугольником является как замкнутая линия, так и эта линия вместе с плоскостью внутри неё.

Такие звенья называются сторонами многоугольника. В нашем случае это стороны АВ, ВС, СD,DE, ЕА.

Углы, образованные двумя соседними сторонами, называют углами многоугольника, а их вершины – вершинами многоугольника.

∠А, ∠В, ∠С, ∠D, ∠E – углы многоугольника

Точки А, В, С, D, E – вершины многоугольника

Кроме того, у многоугольника есть ещё и диагонали.

Диагональ – это отрезок, соединяющий две несмежные вершины многоугольника. АС, СЕ – диагонали.

Сумма всех сторон многоугольника составляет периметр многоугольника.

P = АВ + ВС + СD + DЕ + ЕА

Рассмотрим разновидности многоугольников.

Многоугольник называется выпуклым, если он расположен по одну сторону от каждой прямой, содержащей его сторону.

Например, многоугольник ABCDE – выпуклый. А многоугольник MNKLO – нет.

По числу сторон многоугольники делятся на треугольники, пятиугольники и так далее.

Кроме того, многоугольники, у которых все стороны и все углы равны, называют правильными. Например, квадрат.

Многоугольники можно сравнить путём наложения. Если они полностью накладываются друг на друга, то считаются равными. При этом стоит помнить, они имеют одинаковые площади.

Для определения площади многоугольника надо выяснить, сколько раз выбранная единица измерения содержится в этой фигуре.

Не только человек может рисовать многоугольники. Природа тоже создаёт многоугольники в большом разнообразии. Рассмотрим, где они встречаются. Например, шестиугольники можно увидеть в сотах пчёл и – под микроскопом – в строении глаза мухи или некоторых других насекомых.

Панцирь черепахи тоже изобилует большим количеством многоугольников. Как и кожа змеи: она буквально покрыта многоугольниками. В общем, природа постаралась и разнообразила мир геометрическими фигурами.

№ 1. Чему равен периметр правильного шестиугольника со стороной 4 см?

Решение: для решения этой задачи достаточно вспомнить, что в правильных фигурах все стороны равны, следовательно, все стороны шестиугольника равны 4 см. Вычислим периметр шестиугольника, это сумма всех его сторон.

Р = 4 см + 4 см + 4 см + 4 см + 4 см + 4 см = 24 см

№ 2. Из листа железа размером 10 × 14 см вырезали два квадрата со стороной 4 см и три прямоугольника со сторонами 2см и 6см. Определите площадь остатка.

Решение: сначала найдём площадь листа:

S = 10 cм · 14 см = 140 см 2

Далее вычислим площадь квадратов со сторонами 4см:

S = 4 cм · 4 см = 16 см 2

Тогда площадь двух квадратов равна:

16 см 2 · 2 = 32 см 2

Найдём площадь прямоугольника:

S = 2 cм · 6 см = 12 см 2

Тогда площадь трёх прямоугольников равна:

12 см 2 · 3 = 36 см 2

Определим площади всех квадратов и прямоугольников, вырезанных из листа:

32 см 2 + 36 см 2 = 68 см 2

А теперь найдём площадь остатка: 140 см 2 – 68 см 2 = 72 см 2

Источник

Что такое многоугольник в математике — виды, свойства и примеры фигур с названиями

Геометрическую фигуру, ограниченную со всех сторон ломанной линией, называют многоугольником. В математике такое понятие применимо для множества объектов, образованных из трёх и более отрезков. Фигуры, относящиеся к этому классу, могут иметь как произвольную форму, так и строгую. Например, семиугольник, квадрат. Но при этом их всех объединяют одинаковые свойства и ряд правил.

Общие сведения

Основной линией, с помощью которой образовывается многоугольная фигура, называется ломанная. Это несколько последовательно соединённых между собой отрезков. Если при этом они друг друга не пересекают, кривую считают простой. В ином случае говорят про ломанную с самопересечением. Каждый отрезок, входящий в кривую, называют звеном. Точки, ограничивающие его — вершинами.

Нарисовать ломанную можно по-разному. Главное, соблюдать правило последовательного соединения точек отрезков. Если при этом получится рисунок, на котором первая вершина начального отрезка совпадёт с последней вершиной (ломанная замкнётся), такая кривая называется замкнутой. Но чаще используется другое название — многоугольник. Другими словами, это фигура, образованная соединёнными между собой прямыми, состоящая из отрезков без самопересечения.

Любого вида многоугольник состоит из следующих частей:

Две прямые линии, соединяющиеся у вершины, образуют угол. Он получается при пересечении лучей, проходящих по сторонам фигуры. Именно от количества углов, получаемых при построении, тот или иной геометрический объект может иметь своё уникальное название. Например, тело с тремя углами — треугольник, четырьмя — четырёхугольник, пятью — пятиугольник.

Понятия применимы не только к плоскости, но и к пространству. Так, во втором случае с помощью ломанной образовывается пространственный многоугольник. Его особенность в том, что вершины тела не лежат в одной плоскости и как минимум фигура должна иметь их по меньшей мере 4. Многоугольник с n вершинами называется n—угольником.

Каждая фигура со множеством углов имеет особые линии. Это такие отрезки, построение которых помогает охарактеризовать тело. Одной из них является диагональ. Это элемент, который получается при соединении отрезком двух несоседних вершин. Таких замкнутых прямых в многоугольнике может быть много. При этом из одной вершины можно строить несколько диагоналей.

А также все многоугольники разделяют на 2 типа — выпуклые и невыпуклые. Тело хотя бы с одним углом, смотрящим внутрь, относится ко второму типу, а тот, чьи углы направлены наружу — к первому. В школьном курсе геометрии изучают только второй вид, расположенный на плоскости. Более сложными видами многоугольников занимается стереометрия и планиметрия.

Простейшие четырёхугольники

Любой многоугольник, который состоит из четырёх углов, называют четырёхугольным. Он относится к простейшим геометрическим телам. Если о нём ничего не известно, его считают произвольным, то есть фигурой, у которой нет особенных углов или сторон. В другом случае четырёхугольники имеют собственные названия.

Наиболее часто приходится сталкиваться со следующими видами:

Для всех этих видов характерно, что каждая из фигур имеет 2 пересекающиеся диагонали. Причём точка их соприкосновения делит отрезок на 2 равные части. Кроме этого, для прямоугольника и квадрата длина одной диагонали равна другой. Если у четырёхугольного прямоугольника обозначить стороны a и b, противоположные им грани также будут a и b.

Каждый отрезок, образующий многоугольник, имеет свою длину. При их сложении получается периметр фигуры. Для его обозначения используют заглавную латинскую букву P. Например, если есть многоугольник, образованный сторонами AB, BC, CA, его периметр будет равняться: Pabc = AB + BC + CA. Можно обратить внимание, что количество углов соответствует числу сторон, складываемых для нахождения P. Это важный параметр, позволяющий оценить размер фигуры.

Прямая четырёхугольная фигура является частным случаем ромба. А значит, что все формулы, указанные для квадрата, справедливы и при применении к нему. Следует отметить, что площадь ромба может быть найдена и как половина произведения его диагоналей.

Треугольный многоугольник

Такую фигуру называют треугольником. Она состоит из трёх углов и такого же числа сторон. Их, принято обозначать маленькими буквами a, b, c или подписывать двумя заглавными по названиям вершин, которые являются началом и концом отрезка. Например, треугольник ABC содержит стороны: AB = a, BC = b, AC = c.

В зависимости от особенностей, фигура может называться:

Но несмотря на классификацию, все перечисленные виды обладают общими свойствами. Считается, что угол любого плоского треугольника образуется при пересечении двух лучей, содержащих его стороны, то есть если говорят об ∠A, то подразумевают, что был лучи AB и АС, при построении которых он и образовался. Таким образом, он заключается не между сторонами, а лучами.

Как и для любого другого многоугольника, у треугольника есть периметр и площадь. Следуя из определения первого, для фигуры с вершинами ABC он будет равен сумме длин всех сторон: P = a + b + c. У треугольников существуют так называемые замечательные линии: медиана, биссектриса, высота.

Эти 3 параметра определяют свойства треугольной фигуры. С их помощью можно находить, площадь, стороны, значения углов. Определение медианы звучит так: это прямая, проведённая из угла к противолежащей стороне таким образом, что разделяет её пополам. Под биссектрисой же понимают отрезок, разделяющий угол на 2 равные части. Высотой называют перпендикуляр, опущенный на противоположную сторону из вершины.

Треугольник, который выглядит, как прямой угол, называют прямоугольным. То есть построив в любом многоугольнике с тремя углами высоту, можно получить две фигуры, обе из которых точно будут прямоугольными. Боковые грани, перпендикулярные друг другу, называют катетами, а оставшуюся сторону — гипотенузой. По сути, тело представляет собой разделённый диагональю квадрат. Отсюда площадь многоугольника будет равняться произведению катетов, делённых на 2: S = a*b/2. А также следует отметить, что у равнобедренного треугольника медиана, высота и биссектриса совпадают.

Теорема об углах

Многоугольники бывают выпуклые и вогнутые. Чтобы узнать, какой из них приходится рассматривать в том или ином случае, можно сделать следующее. Через каждую сторону провести прямую. Если по отношению к любой из них фигура будет лежать в одной полуплоскости относительно неё, многоугольник считается выпуклым, в ином случае — вогнутым.

Для первого типа существуют важные соотношения. Пусть имеется произвольный многоугольник. Интерес представляет сумма всех его углов. Посчитать её можно следующим образом. Нужно взять любую вершину и соединить её со всеми оставшимися прямой линией. В результате получится несколько треугольников. Затем нужно посчитать их количество. Например, в шестиугольнике их будет 4, восьмиугольнике — 6. Это число легко находится, так как существует правило, согласно которому в любой n-угольной фигуре можно построить n-2 треугольника.

Источник

Многоугольники (ЕГЭ 2022)

Никогда не было интересно, почему в треугольнике 180 градусов?

А в других фигурах сколько? Да постой, положи транспортир!

Сейчас ты узнаешь много нового о такой, казалось бы, простой теме, как многоугольники.

Многоугольники — коротко о главном

Многоугольник – это замкнутая линия, которая образовывается, если взять \( \displaystyle n\) каких-либо точек \( \displaystyle <_<1>>,\text< ><_<2>>,\text< >…,

Многоугольник с \( \displaystyle n\) сторонами называют \( \displaystyle n\)-угольником.

Например: многоугольник c \( \displaystyle 4\) сторонами называют четырехугольником, многоугольник с \( \displaystyle 6\) сторонами — шестиугольником и так далее по аналогии.

Выпуклый многоугольник – многоугольник лежащий по одну сторону от любой прямой, соединяющей его соседние вершины.

Сумма внутренних углов выпуклого n-угольника равна \( \displaystyle 180<>^\circ \cdot (n-2)\) или \( \displaystyle <<\alpha >_<1>>+<<\alpha >_<2>>+\text< >…

Правильный выпуклый многоугольник – многоугольник все стороны и внутренние углы которого равны.

Внутренний угол правильного \( \displaystyle n\)-угольника равен \( \displaystyle \alpha =\frac\cdot 180<>^\circ \).

Любой правильный многоугольник можно вписать в окружность и вокруг любого правильного многоугольника можно описать окружность.

Центры вписанной в правильный многоугольник окружности и окружности, описанной около него, совпадают.

Если многоугольник такой, что в него можно вписать окружность, то его площадь выражается формулой: \( \displaystyle S=pr\), где \( \displaystyle p=\frac<<_<1>><_<2>>+<_<2>><_<3>>+…+<_><_<1>>><2>\).

Многоугольник — подробнее

Многоугольник – это замкнутая линия, которая образовывается, если взять \( \displaystyle n\) каких-либо точек \( \displaystyle <_<1>>,\text< ><_<2>>,\text< >…,

При этом смежные стороны (имеющие общую вершину) не должны лежать на одной прямой, а несмежные стороны не должны иметь общих точек (то есть не должны пересекаться).

Многоугольник с \( \displaystyle n\) сторонами называют \( \displaystyle n\)-угольником.

Произвольные многоугольники

Давай-ка нарисуем, какие бывают многоугольники.

А теперь вопрос: какой из этих многоугольников выпадает из ряда?

Посмотри внимательно на второй многоугольник — он отличается от всех остальных. Чем же?

Это не выпуклый многоугольник. Это, конечно, математическое название, но с человеческой интуицией не расходится.

Ну вот, а мы будем рассматривать только выпуклые многоугольники, то есть такие, как 1),3),4) и т.п.

Итак, основной факт:

В любом многоугольнике сумма внутренних углов равна \( \displaystyle 180^o(n-2)\), где буква «\( \displaystyle n\)» означает число углов многоугольника.

Давай сразу к примерам:

Четырехугольник

Пятиугольник

Шестиугольник

Ах да, про треугольник забыли.

Треугольник

Сумма углов многоугольника. Доказательство.

А теперь давай все-таки разберемся, откуда же взялась формула суммы углом многоугольника \( \displaystyle 180^\circ(n-2)\).

Понимаешь, приемчик, который мы сейчас применим, часто оказывается полезным при решении разных задач.

Несмотря на то, что теорема о сумме углов многоугольника верна для всякого многоугольника, доказательство красивое и простое только для выпуклых многоугольников.

Итак, давай разделим многоугольник на треугольники.

Вот так: из одной точки проведем все диагонали, что можно. Сколько их будет? Считаем:

Всего вершин: \( \displaystyle n\)

Из вершины \( \displaystyle B\) можем провести диагонали во все вершины, кроме:

Значит всего диагоналей \( \displaystyle (n-3)\). А на сколько треугольников распался наш многоугольник?

Представь себе: на \( \displaystyle n-2\). Порисуй, посчитай – удостоверься, что треугольников оказывается ровно на один больше.

Итак, у нас ровно \( \displaystyle n-2\) треугольника. И сумма углов многоугольника просто равна сумме углов треугольников, на которые мы разбили многоугольник.

Чему равна сумма углов треугольника? Помнишь? Конечно \( \displaystyle 180<>^\circ \).

Ну вот, \( \displaystyle n-2\) треугольника, в каждом по \( \displaystyle 180<>^\circ \), значит:

Сумма углов многоугольника равна \( \displaystyle 180<>^\circ \)\( \displaystyle (n-2)\)

Что же из этого может оказаться полезным? Два момента:

Читать далее…

Чтобы пользоваться учебником ЮКлэва без ограничений, зарегистрируйтесь один раз:

Правильные многоугольники

Многоугольник называется правильным, если все его углы и все его стороны равны.

Так, например: квадрат – правильный четырехугольник, а вот прямоугольник – нет, хоть и все углы у него равные, и ромб – нет, хоть и все стороны равны. Нужно непременно, чтобы все углы и все стороны были равны.

Первый вопрос:

А можно ли найти величину одного (а значит и всех) угла правильного многоугольника?

Давай посмотрим на примере.

Пусть есть, скажем, правильный восьмиугольник:

Сумма всех его углов равна \( \displaystyle 180<>^\circ \left( 8-2 \right)=1080<>^\circ \).

А сколько всего углов? Восемь конечно, и они все одинаковые.

Значит любой угол, скажем \( \displaystyle \angle A\) можно найти:

\( \displaystyle \angle A=\frac<1080<>^\circ ><8>=135<>^\circ \).

Что мы еще должны знать?

Любой правильный многоугольник можно вписать в окружность и вокруг любого правильного многоугольника можно описать окружность.

При этом центры этих окружностей совпадают.

Смотри, как это выглядит!

И более того, всегда можно посчитать соотношение между радиусом вписанной и описанной окружностей.

Давай опять на примере восьмиугольника.

Посмотри на \( \displaystyle \Delta OKG\). В нем \( \displaystyle OK=r,OG=R.\)

Значит, \( \displaystyle \frac=\sin \angle x\) – и это не только в восьмиугольнике!

Чему же равен в нашем случае \( \displaystyle \angle x\)?

Ровно половине \( \displaystyle \angle G\), представь себе!

Значит \( \displaystyle \angle x=\frac<135<>^\circ ><2>=67,5<>^\circ \).

Смешно? Но так и есть! Поэтому для восьмиугольника \( \displaystyle \frac=\sin 67,5<>^\circ \).

Может возникнуть еще один вопрос: а можно ли посчитать углы «около» точки \( \displaystyle O\)?

И тот же ответ: конечно можно!

Опять рассмотрим наш восьмиугольник. Вот мы хотим найти \( \displaystyle \angle \alpha\) (то есть \( \displaystyle \angle HOG\)).

Читать далее…

Чтобы пользоваться учебником ЮКлэва без ограничений, зарегистрируйтесь один раз:

И так можно все находить не только для восьмиугольника, но и для любого правильного многоугольника.

Бонус. Вебинар из нашего курса подготовки к ЕГЭ по математике

ЕГЭ 6. Описанная окружность. Многоугольники

Вы этом видео вы узнаете, что такое описанная окружность, где находится её центр, и другие свойства.

Около каких фигур можно, а вокруг каких нельзя описать окружность.

Также мы узнаем, что такое правильные многоугольники, и какие у них свойства; как они связаны с описанной окружностью.

Научимся решать задачи из ЕГЭ на описанную окружность и правильные многоугольники.

Наши курсы по подготовке к ЕГЭ по математике, информатике и физике

Курсы для тех, кому нужно получить 90+ и поступить в топовый ВУЗ страны.

А теперь твоя очередь!

Теперь ты знаешь все о многоугольниках!

Особенно эти знания пригодятся тебе, когда будешь решать задачи про окружности. Задачи олимпиадного уровня. Да и просто так знать полезно 🙂

А сейчас мы хотим услышать тебя. Понравилась ли тебе статья? Ты во всем разобрался?

Кстати, пытался строить многоугольники циркулем?

Напиши в комментариях ниже!

И задай любые вопросы, если они возникли! Мы непременно ответим!

Добавить комментарий Отменить ответ

3 комментария

Як разбить чатырох угольник так, чтоб палучился трохвугольник и чатырохвугольник

Даша, например, можно провести отрезок из вершины в середину противоположной стороны.

Некоторые комментарии прошлых лет к этой статье:

Сергей
19 февраля 2018
Просто огромное спасибо. Хоть что-то начал понимать.

Александр (админ)
19 февраля 2018
Просто огромное пожалуйста. 🙂 Очень приятно слышать от вас такие слова.

Вероника
18 марта 2020
Спасибо большое, а то на карантине приходится самим разбирать темы!

Александр (админ)
18 марта 2020
Отлично, Вероника! Круто, что ты сама пытаешься разобраться с математикой! Этот навык ой как пригодится в будущем. Я всегда говорю: «В жизни репетитора и учителя рядом не будет». И я рад, что наш скромный сайт в этом помогает. Удачи на экзаменах! Все будет хорошо!

Сима
01 июля 2020
Блин, действительно очень круто изложили. А главное- понятно и просто. Начала подготовку к егэ, в следующем году сдавать. Очень помогли разобраться с этой темой! Спасибо)

Александр (админ)
01 июля 2020
Блин, Сима, до чертиков приятно слышать такие слова! 🙂 Если начала подготовку к ЕГЭ, то будь на связи, мы сейчас делаем крутейший курс подготовки к ЕГЭ, где вот так вот просто все будет объяснять Алексей Шевчук.

Записаться на курсы:

Источник