чем больше момент сопротивления тем

Значение пластического момента сопротивления

Здравствуйте уважаемые форумчане.

Подскажите ответ на два небольших вопроса.

1. Во сколько раз пластический момент сопротивления может быть больше упругого?

Размеры, (мм)
полка b =102 tf=16
стенка h=380 tw=13,5

Площадь поперечного сечения A, (мм кв) 7962,00
Центр тяжести (мм), xc=24,89, yc=190,00
Момент инерции Ix,(см 4) 15559,858
Момент инерции Iy, (см 4) 667,233
Момент сопротивления сечения Wx, (см 3) 818,940
Момент сопротивления сечения Wy, (см 3) 86,530
Статический момент полусечения Sx’, (см 3) 501,387
Статический момент полусечения Sy’, (см 3) 95,135
Пластический момент сопротивления сечения Wplx (см 3) 1002,774
Пластический момент сопротивления сечения Wply (см 3) 190,270

Wplx/Wx 1,224
Wply/Wy 2,199

Получается больше чем в 2 раза, такое бывает или Я где-то ошибся при расчете.

2. Нет ли ошибки в сортаментах?

ГОСТ 8240
N 26 C
Момент сопротивления сечения Wy, (см 3) 171,600 – должно быть около 24.

Момент сопротивления сечения Wy, (см 3) 33,17 – должно быть около 13.
310х100х6

Момент сопротивления сечения Wx, (см 3) 54,777 – должно быть около 260.

Документооборот и управление

У меня так и считает

Wpl=2 * S’. Ось, через центр тяжести.

У двутавра проблем нет считает, почти с совпадением с сортаментом.

Проблема с швеллером, относительно оси y-y, иногда больше 2 получается.

Может так и есть для оси y-y

Формулы для швеллера приложены

— если форма сечения произвольна, то в любое количество раз.

Спасибо за ответы.
Попробую спросить по другому.

1. Это правильный расчет характеристик сечения «швеллер»?

Размеры, (мм) b=100 h=300 tw=15 tf=20
Площадь поперечного сечения A, (мм кв) 7900,00
Центр тяжести (мм), xc=29,02, yc=150,00
Момент инерции Ix,(см 4) 10050,333
Момент инерции Iy, (см 4) 697,323
Момент сопротивления сечения Wx, (см 3) 670,022
Момент сопротивления сечения Wy, (см 3) 98,241
Статический момент полусечения Sx’, (см 3) 406,750
Статический момент полусечения Sy’, (см 3) 100,766
Пластический момент сопротивления сечения Wplx (см 3) 813,500
Пластический момент сопротивления сечения Wply (см 3) 201,532
Wplx/Wx 1,214
Wply/Wy 2,051

Размеры, (мм) b=300 h=200 tw=15 tf=20
Площадь поперечного сечения A, (мм кв) 8700,00
Центр тяжести (мм), yc=158,97
Момент инерции Ix,(см 4) 2611,069
Момент инерции Iy, (см 4) 4505,063
Момент сопротивления сечения Wx, (см 3) 164,254
Момент сопротивления сечения Wy, (см 3) 300,337
Статический момент полусечения Sx’, (см 3) 189,525
Статический момент полусечения Sy’, (см 3) 230,063
Пластический момент сопротивления сечения Wplx (см 3) 379,051
Пластический момент сопротивления сечения Wply (см 3) 460,125
Wplx/Wx 2,308
Wply/Wy 1,532

Если не правильно, то где?

Wpl=Z*Aч=(Z+)*(A+) +(Z-)*(A-)= (S+’)+(S-‘), если ось главная центральная (S+’)=(S-‘)=S’

S+’, S-‘ это статический момент полусечения сжатой и растянутой части

меня теория не интересует.

Я просто хочу узнать во сколько раз пластический момент больше упругого относительно главных центральных осей у конкретного асимметричного сечения швеллера или тавра или например уголка.

Размеры, (мм) b=206 h=213 tw=20 tf=15
Площадь поперечного сечения A, (мм кв) 7050,00

Центр тяжести (мм), xc=50,76, yc=67,32
Момент инерции Ix,(см 4) 3268,154
Момент инерции Iy, (см 4) 2607,099
Момент сопротивления сечения Wx, (см 3) 224,340
Момент сопротивления сечения Wy, (см 3) 167,942
Статический момент полусечения Sx, (см 3) 212,223
Статический момент полусечения Sy, (см 3) 180,742
Пластический момент сопротивления сечения Wplx (см 3) 424,446
Пластический момент сопротивления сечения Wply (см 3) 361,484
Wplx/Wx 1,892
Wply/Wy 2,152

Источник

Моменты сопротивления составных сечений.

Для вашего тавра это делается так:
1. Найти центр тяжести составного сечения. Надеюсь, вы знаете как это делается.
2.Вы уже разбили составное сечение на простые фигуры. Теперь надо найти моменты инерции этих фигур относительно главных центральных осей всего составного сечения. Они идут через центр тяжести всего составного сечения. Надеюсь вы знаете как находить момент инерции фигуры относительно смещенных осей или еще и повернутых осей.
3. Момент инерции составного сечения (назовем его Y1) равен сумме вот этих найденных вами моментов инерции составляющих его фигур(частей) относительно главных центральных осей всего составного сечения.
4.Зная положение центра тяжести составного сечения и рассматривая его конкретную главную центральную ось (одну из двух, которая вас интересует), определяете наибольшее из расстояний от этой оси до края составного сечения. Назовем это расстояние Н1.
5. Момент сопротивления составного сечения W1=Y1/H1. Это и будет минимальный W.
6. В принципе можно повторить два последних пункта, но искать теперь расстояние от интересовавшей вас главной центральной оси до противоположного первому варианту края сечения. Назовем это расстояние Н2.
7. Тогда найденный W2=Y1/H2 будет максимальный W.

Все это подробно описано, например, в «Справочнике по сопротивлению материалов» под редакцией Писаренко (есть в даунлоаде http://dwg.ru/dnl/5056).

Для вашего тавра это делается так:
1. Найти центр тяжести составного сечения. Надеюсь, вы знаете как это делается.
2.Вы уже разбили составное сечение на простые фигуры. Теперь найдо найти моменты инерции этих фигур относительно главных центральных осей всего составного сечения. Они идут через центр тяжести всего составного сечения. Надеюсь вы знаете как находить момент инерции фигуры относительно смещенных осей или еще и повернутых осей.
3. Момент инерции составного сечения (назовем его Y1) равен сумме вот этих найденных вами моментов инерции составляющих его фигур(частей) относительно главных центральных осей всего составного сечения.
4.Зная положение центра тяжести составного сечения и рассматривая его конкретную главную центральную ось (одну из двух, которая вас интересует), определяете наибольшее из расстояний от этой оси до края составного сечения. Назовем это расстояние Н1.
5. Момент сопротивления составного сечения W=Y1/H1.

Все это подробно описано, например, в «Справочнике по сопротивлению материалов» под редакцией Писаренко (есть в даунлоаде).

обозначение ед. изм.
см
ширина сжатой полки bfґ 19.9
ширина растянутой полки bf 19.9
толщина сжатой полки hfґ 1.1
толщина растянутой полки hf 1.1
высота стенки hст 37.4
толщина стенки tст 0.7
радиус закругления R 1.6
модуль юнга E 2000000
расчётное сопротивление Ry 2450

общая высота сечения h h=hст+hf+hfٰ 39.6
площадь «антисекториального треугольника» радиусом R AR AR=R^2*(1-π/4) 0.549380702
площадь сечения растянутого пояса Af Af=hf*bf 21.89
площадь сечения сжатого пояса Afٰ Afٰ=hfٰ*bfٰ 21.89
площадь сечения стенки Aст Aст=hст*tст 26.18
площадь всего сечения A A=hст*tст+hf*bf+hfٰ*bfٰ+4*AR 72.15752281
своя ордината центра тяжести «антисекториального треугольника» YR собств YR собств=R/(6-3*π/2) 1.242611298
расстояние от центра тяжести стенки до нижней оси Yст Yст=hст/2+hf 19.8
расстояние от центра тяжести сжатой полки до нижней оси Yfґ Yfґ=h-hfґ/2 39.05
расстояние от центра тяжести растянутой полки до нижней оси Yf Yf=hf/2 0.55
расстояние от центра тяжести сжатых треугольников до нижней оси YR,totґ YRґ=hf+hст-R+YR 38.1426113
расстояние от центра тяжести растянутых треугольников до нижней оси YR, tot YR, tot=hf+R-YR 1.457388702
статический момент сжатой полки относительно нижней оси Sfґ Sґ=Afٰ*Yfґ 854.8045
статический момент растянутой полки относительно нижней оси Sf Sf=Af*Yf 12.0395
статический момент стенки относительно нижней оси Sст Sст=Aст*Yст 518.364
статический момент растянутых треугольников относительно нижней оси SR SR=2*AR*YR, tot 1.601322456
статический момент сжатых треугольников относительно нижней оси SRґ SRґ=2*AR*YR, totґ 41.90962912
статический момент всего сечения относительно нижней оси S S=Sfґ+Sf+Sст+SR+SRґ 1428.718952
положение нейтральной оси y y=S/A 19.8
собственный момент инерции сжатой полки Ifґсобств x Ifґсобств x=bfٰ*hfٰ^3/12 2.207241667
собственный момент инерции растянутой полки If собств x If собств x=bf*hf^3/12 2.207241667
собственный момент инерции стенки Iст собств x Iст собств x=tст*hст^3/12 3051.628067
собственными моментами инерции треугольников пренебрегаем
расстояние от центра тяжести растянутого пояса до центра тяжести сечения yf yf=y-hf/2 19.25
расстояние от центра тяжести сжатого пояса до центра тяжести сечения yfґ yfґ=h-y-hfґ/2 19.25
расстояние от центра тяжести стенки до центра тяжести сечения yст yст=y-hст/2-hf 4.88498E-15
расстояние от центра тяжести сжатых треугольников до центра тяжести сечения yRґ yRґ=YR,totґ-y 18.3426113
расстояние от центра тяжести растянутых треугольников до центра тяжести сечения yR yR=y-hf-R+YR собств 18.3426113
«дополнительный» момент инерции растянутой полки If доп If доп=yf^2*Af 8111.613125
«дополнительный» момент инерции сжатой полки If допґ If допґ=yfґ^2*Afґ 8111.613125
«дополнительный» момент инерции стенки Iст доп Iст доп=yст^2*Aст 6.24734E-28
«дополнительный» момент инерции сжатых треугольников IR допґx IR допґx=(yRґ)^2*2*AR 369.6798006
«дополнительный» момент инерции растянутых треугольников IR доп x IR доп x=(yR)^2*2*AR 369.6798006
полный момент инерции сечения Ix 20018.6284
момент сопротивления растянутых волокон Wраст x Wраст x=Ix/y 1011.041838
момент сопротивления сжатых волокон Wсжат x Wсжат x=Ix/(h-y) 1011.041838
радиус инерции относительно оси x ix ix=(Ix/A)^0.5 16.65621627

момент инерции верхнего пояса относительно оси y-y Ifґy Ifґy=hfґ*bfґ^3/12 722.3882417
момент инерции нижнего пояса относительно оси y-y If y If y=hf*bf^3/12 722.3882417
момент инерции стенки относительно оси y-y Iст y Iст y=hст*tст^3/12 1.069016667
расстояние от центра тяжести сжатых треугольников до оси y-y xR xR=R-YR собств+tст/2 0.707388702
момент инерции всех треугольников относительно вертикальной оси y-y IR y IR y=4*AR*xR^2 1.099637723
момент инерции всего сечения относительно вертикальной оси y-y I y 1446.945138
максимальная ширина сечения (какой из поясов больше) x x=max(bf;bfґ) 19.9
момент сопротивления всего сечения относительно вертикальной оси y-y Wy Wy=Iy(x/2) 145.4216219
радиус инерции относительно оси y iy iy=(Iy/A)^0.5 4.478011708

Источник

Лекция 5. Моменты инерции поперечного сечения

Иногда при расчете строительных конструкций необходимо знать значение момента инерции поперечного сечения. При этом само понятие момент инерции знает любой инженер, а вот откуда взялось это понятие, и какой его физический смысл, могут объяснить не многие. Как правило в любом справочнике или учебнике по сопротивлению материалов дается приблизительно следующее определение для момента инерции:

I = ∑r_i 2 dF i =∫r 2 dF (1.1)

В принципе и определение и формула, его описывающая, не сложные и запомнить их намного легче, чем вникнуть в суть. Но все-таки попробуем разобраться, что же такое момент инерции и откуда он взялся.

Понятие момент инерции пришло в сопромат и строительную механику из другого раздела физики, изучающего кинематику движения, в частности вращательное движение. Но все равно начнем издалека.

Я точно не знаю, упало ли Исааку Ньютону на голову яблоко, упало оно рядом, или вообще не падало, теория вероятности допускает все эти варианты (к тому же в этом яблоке слишком много от библейской легенды о древе познания), однако я уверен, что Ньютон был наблюдательным человеком, способным делать выводы из своих наблюдений. Так наблюдательность и воображение позволили Ньютону сформулировать основной закон динамики (второй закон Ньютона), согласно которому масса тела m, умноженная на ускорение a, равна действующей силе Q (вообще-то более привычным для силы является обозначение F, но так как дальше мы будем иметь дело с площадью, которая также часто обозначается как F, то я использую для внешней силы, рассматриваемой в теоретической механике как сосредоточенная нагрузка, обозначение Q, сути дела это не меняет):

Q = ma (1.2)

По мне величие Ньютона именно в простоте и понятности данного определения. А еще, если учесть, что при равноускоренном движении ускорение а равно отношению приращения скорости ΔV к периоду времени Δt, за который скорость изменилась:

при V_о = 0 a = v/t (1.3.2)

то можно определить основные параметры движения, такие как расстояние, скорость, время и даже импульс р, характеризующий количество движения:

p = mv (1.4)

Например, яблоко, падающее с разной высоты под действием только силы тяжести, будет падать до земли разное время, иметь разную скорость в момент приземления и соответственно разный импульс. Другими словами, яблоко, падающее с бóльшей высоты, будет дольше лететь и сильнее треснет по лбу незадачливого наблюдателя. И все это Ньютон свел к простой и понятной формуле.

А еще Ньютон сформулировал закон инерции (первый закон Ньютона): если ускорение а = 0, то в инерциальной системе отсчета невозможно определить, находится ли наблюдаемое тело, на которое не действуют внешние силы, в состоянии покоя или движется прямолинейно с постоянной скоростью. Это свойство материальных тел сохранять свою скорость, пусть даже и нулевую, называется инертностью. Мерой инертности является инерционная масса тела. Иногда инерционная масса называется инертной, но сути дела это не меняет. Считается, что инерционная масса равна гравитационной массе и потому часто не уточняется, какая именно масса имеется в виду, а упоминается просто масса тела.

Не менее важным и значимым является и третий закон Ньютона, согласно которому сила действия равна силе противодействия, если силы направлены по одной прямой, но при этом в противоположные стороны. Не смотря, на кажущуюся простоту, и этот вывод Ньютона гениален и значение этого закона трудно переоценить. Об одном из применений этого закона чуть ниже.

Однако данные положения справедливы только для тел, движущихся поступательно, т.е. по прямолинейной траектории и при этом все материальные точки таких тел двигаются с одинаковой скоростью или одинаковым ускорением. При криволинейном движении и в частности при вращательном движении, например, когда тело вращается вокруг своей оси симметрии, материальные точки такого тела перемещаются в пространстве с одинаковой угловой скоростью w, но при этом линейная скорость v у различных точек будет разная и эта линейная скорость прямо пропорциональна расстоянию r от оси вращения до этой точки:

v = wr (1.5)

при этом угловая скорость равна отношению приращения угла поворота Δφ к периоду времени Δt, за который угол поворота изменился:

при φ_о = 0 w = φ/t (1.7.2)

соответственно нормальное ускорение а_n при вращательном движении равно:

a_n = v 2 /r = w 2 r (1.8)

И получается, что для вращательного движения мы не можем прямо использовать формулу (1.2), так как при вращательном движении одного только значения массы тела недостаточно, требуется еще знать распределение этой массы в теле. Получается, что чем ближе материальные точки тела к оси вращения, тем меньшую силу требуется приложить, чтобы заставить тело вращаться и наоборот, чем дальше материальные точки тела от оси вращения, тем большую силу нужно приложить, чтобы заставить тело вращаться (в данном случае речь идет о приложении силы в одной и той же точке). К тому же при вращении тела более удобно рассматривать не действующую силу, а вращающий момент, так как при вращательном движении точка приложения силы также имеет большое значение.

Поразительные свойства момента нам известны со времен Архимеда и если применить понятие момента к вращательному движению, то значение момента М будет тем больше, чем больше расстояние r от оси вращения до точки приложения силы F (в строительной механике внешняя сила часто обозначается как Р или Q):

М = Qr (1.9)

Из этой также не очень сложной формулы выходит, что если сила будет приложена по оси вращения, то никакого вращения не будет, так как r = 0, а если сила будет приложена на максимальном удалении от оси вращения, то и значение момента будет максимальным. А если мы подставим в формулу (1.9) значение силы из формулы (1.2) и значение нормального ускорения и формулы (1.8), то получим следующее уравнение:

М = mw 2 r·r = mw 2 r 2 (1.10)

В частном случае когда тело является материальной точкой, имеющей размеры намного меньше, чем расстояние от этой точки до оси вращения, уравнение (1.10) применимо в чистом виде. Однако для тела, вращающегося вокруг одной из своих осей симметрии, расстояние от каждой материальной точки составляющей данное тело, всегда меньше одного из геометрических размеров тела и потому распределение массы тела имеет большое значение, в этом случае требуется учесть эти расстояния отдельно для каждой точки:

M = ∑r i 2 w 2 m_i (1.11.1)

И тогда получается, что согласно третьему закону Ньютона в ответ на действие вращающего момента будет возникать так называемый момент инерции I. При этом значения вращающего момента и момента инерции будут равны, а сами моменты направлены в противоположные стороны. При постоянной угловой скорости вращения, например w = 1, основными величинами, характеризующими вращающий момент или момент инерции будут масса материальных точек, составляющих тело, и расстояния от этих точек до оси вращения. В итоге формула момента инерции примет следующий вид:

I_c = ∫ρr 2 dV (1.13)

Таким образом момент инерции является мерой инертности тела при вращательном движении, подобно тому как масса является мерой инертности тела при поступательном прямолинейном движении.

Все круг замкнулся. И тут может возникнуть вопрос, какое отношение все эти законы динамики и кинематики имеют к расчету статических строительных конструкций? Оказывается, что ни на есть самое прямое и непосредственное. Во-первых потому, что все эти формулы выводились физиками и математиками в те далекие времена, когда таких дисциплин, как «Теоретическая механика» или «Теория сопротивления материалов» попросту не существовало. А во-вторых потому, что весь расчет строительных конструкций и построен на основе указанных законов и формулировок и пока ни кем не опровергнутом утвержении о равенстве гравитационной и инертой масс. Вот только в теории сопротивления материалов все еще проще, как ни парадоксально это звучит.

I_р = ∫r 2 dF (2.1) → (1.1)

Так как в теории сопротивления материалов часто рассматриваются прямоугольные сечения, да и прямоугольная система координат более удобна, то при решении задач обычно рассматриваются два осевых момента инерции поперечного сечения:

I_z = ∫y 2 dF (2.2.1)

I_y = ∫z 2 dF (2.2.2)

Рисунок 1. Значения координат при определении осевых моментов инерции.

В то же время теория сопротивления материалов рассматривает именно поперечное сечение, для которого важны ширина и высота, а длина не учитывается. Само собой при решении задач теории сопротивления материалов, также порой достаточно сложных используются все те же привычные оси х и у. Мне такое положение дел кажется не совсем правильным, так как не смотря на разницу, это все же смежные задачи и потому будет более целесообразным использование единых осей для рассчитываемой конструкции.

Значение полярного момента инерции в прямоугольной системе координат будет:

I_р = ∫r 2 dF = ∫y 2 dF + ∫z 2 dF (2.3)

I_xz = ∫xzdF (2.4)

Среди осей прямоугольной системы координат, проходящих через центр тяжести поперечного сечения, есть две взаимно-перпендикулярные оси, относительно которых осевые моменты инерции принимают максимальное и минимальное значение, при этом центробежный момент инерции сечения I_zy = 0. Такие оси называют главными центральными осями поперечного сечения, а моменты инерции относительно таких осей – главными центральными моментами инерции

Когда в теории сопротивления материалов речь заходит о моментах инерции, то как правило в виду имеются именно главные центральные моменты инерции поперечного сечения. Для квадратных, прямоугольных, круглых сечений главные оси будут совпадать с осями симметрии. Моменты инерции поперечного сечения также называют геометрическими моментами инерции или моментами инерции площади, но суть от этого не изменяется.

I = I_c + r 2 F (2.5)

и тогда полярный статический момент поперечного сечения будет:

S_р = ∫rdF (2.7)

Как видим, определение статического момента сходно с определением момента инерции. Но есть и принципиальная разница. Статический момент потому и называется статическим, что для тела, на которое действует сила тяжести, статический момент равен нулю относительно центра тяжести. Другими словами такое тело находится в состоянии равновесия, если опора приложена к центру тяжести тела. А согласно первому закону Ньютона такое тело или находится в состоянии покоя или движется с постоянной скоростью, т.е. ускорение = 0. А еще с чисто математической точки зрения статический момент может быть равен нулю по той простой причине, что при определении статического момента необходимо учитывать направление действия момента.

S_z = ∫ydF = 0 (2.8)

А еще этот великий ноль позволяет определять опорные реакции строительных конструкций. Если рассматривать строительную конструкцию, к которой приложена например сосредоточенная нагрузка Q в некоторой точке, то такую строительную конструкцию можно рассматривать, как тело с центром тяжести в точке приложения силы, а опорные реакции в этом случае рассматриваются, как силы приложенные в точках опор. Таким образом зная значение сосредоточенной нагрузки Q и расстояния от точки приложения нагрузки до опор строительной конструкции, можно определить опорные реакции.

Например для шарнирно опертой балки на двух опорах значение опорных реакций будет пропорционально расстоянию до точки приложения силы, а сумма реакций опор будет равна приложенной нагрузке. Но как правило при определении опорных реакций поступают еще проще: за центр тяжести принимается одна из опор и тогда сумма моментов от приложенной нагрузки и от остальных опорных реакций все равно равна нулю. В этом случае момент от опорной реакции относительно которой составляется уравнение моментов, равен нулю, так как плечо действия силы = 0, а значит в сумме моментов остаются только две силы: приложенная нагрузка и неизвестная опорная реакция (для статически определимых конструкций).

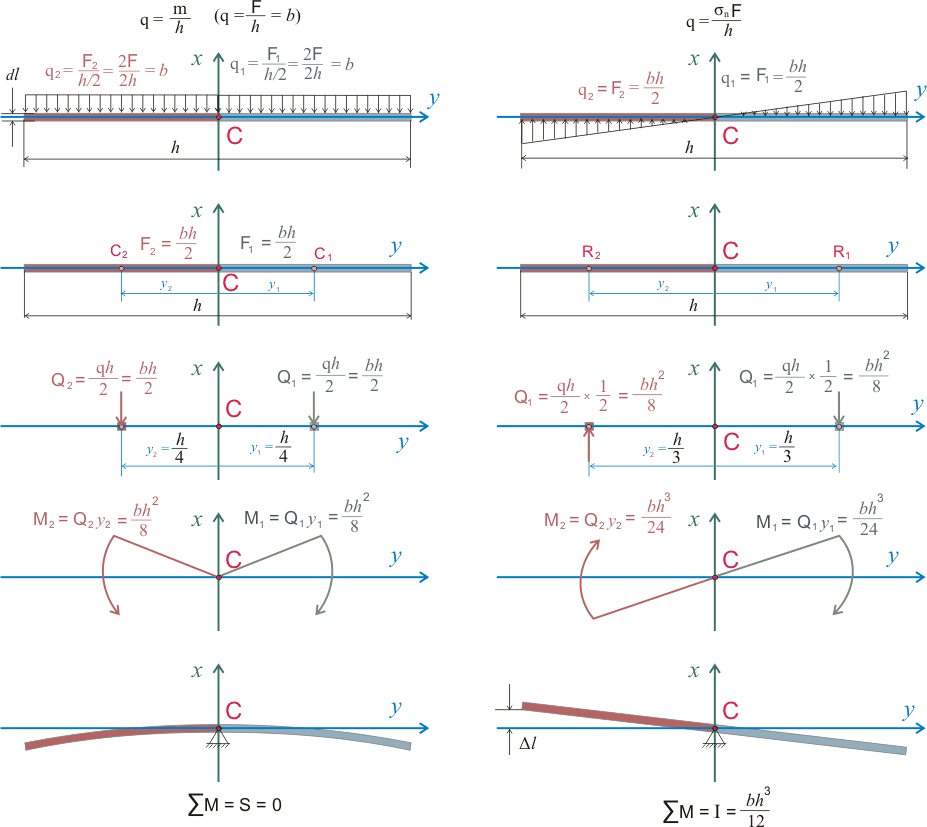
Таким образом принципиальная разница между статическим моментом и моментом инерции в том, что статический момент характеризует сечение, которое сила тяжести как бы пытается сломать пополам относительно центра тяжести или оси симметрии, а момент инерции характеризует тело, все материальные точки которого перемещаются (или пытаются переместиться в одном направлении). Возможно, более наглядно представить себе эту разницу помогут следующие достаточно условные расчетные схемы для прямоугольного сечения:

Рисунок 2. Наглядная разница между статическим моментом и моментом инерции.

А теперь вернемся еще раз к кинематике движения. Если проводить аналогии между напряжениями, возникающими в поперечных сечениях строительных конструкций, и различными видами движения, то в центрально растягиваемых и центрально сжатых элементах возникают напряжения равномерные по всей площади сечения. Эти напряжения можно сравнить с действием некоторой силы на тело, при котором тело будет двигаться прямолинейно и поступательно. А самое интересное, это то, что поперечные сечения центрально-растянутых или центрально сжатых элементов действительно движутся, так как действующие напряжения вызывают деформации. И величину таких деформаций можно определить для любого поперечного сечения конструкции. Для этого достаточно знать значение действующих напряжений, длину элемента, площадь сечения и модуль упругости материала, из которого изготовлена конструкция.

А еще момент инерции позволяет определить момент сопротивления сечения. Для этого момент инерции нужно просто разделить на расстояние от центра тяжести сечения до наиболее удаленной точки сечения, для прямоугольного сечения на h/2. А так как исследуемые сечения не всегда симметричны, то значение момента сопротивления может быть разным для разных частей сечения.

А началось все с банального яблока. хотя нет, начиналось все со слова.

Доступ к полной версии этой статьи и всех остальных статей на данном сайте стоит всего 30 рублей. После успешного завершения перевода откроется страница с благодарностью, адресом электронной почты и продолжением статьи. Если вы хотите задать вопрос по расчету конструкций, пожалуйста, воспользуйтесь этим адресом. Зараннее большое спасибо.)). Если страница не открылась, то скорее всего вы осуществили перевод с другого Яндекс-кошелька, но в любом случае волноваться не надо. Главное, при оформлении перевода точно указать свой e-mail и я обязательно с вами свяжусь. К тому же вы всегда можете добавить свой комментарий. Больше подробностей в статье «Записаться на прием к доктору»

Для терминалов номер Яндекс Кошелька 410012390761783

Номер карты Ymoney 4048 4150 0452 9638 SERGEI GUTOV

Классная статья, всё понятно, с рисунками, красота!

В данной статье сказано: Получается, что чем ближе материальные точки тела к оси вращения, тем меньшую силу требуется приложить, чтобы заставить тело вращаться и наоборот, чем дальше материальные точки тела от оси вращения, тем большую силу нужно приложить, чтобы заставить тело вращаться.
Не наоборот ли? Ведь расстояние от оси является плечом. Чем больше плечо, тем меньше силы нужно приложить для того, чтобы заставит тело вращаться. Или я вновь неправильно всё понял. Упс:(

Возможно я недостаточно ясно выразился, поэтому внес в статью соответствующую поправку. В данном случае речь идет о силе, приложенной в одной и той же точке. Например в первом случае, когда материальная точка расположена близко к центру вращения, то необходимая для вращения сила, приложенная на таком же расстоянии, будет одной. Во втором случае плечо приложения силы не изменится, а вот материальная точка будет от центра вращения значительно дальше, поэтому и сила для ее вращения потребуется больше, хотя при этом масса материальных точек в обоих случаях остается одинаковой.
Надеюсь, теперь понятно объяснил.

То самое объяснение которое так долго я искал. Лучшее на мой взгляд. Спасибо, стало все гораздо яснее!

Рад был помочь, пусть и виртуально.

Здравствуйте!
Вы пишите «соответственно нормальное ускорение аn при вращательном движении равно». На основании чего это соответственно? Для наблюдателя никакого соответствия не видно. Просто в воздухе возникла формула.

Дмитрий, искренне рад, что статья вам понравилась.

Уважаемый Доктор, а Вы не думали выпустить свои труды в печатном виде?

Не думаю, что это будет иметь успех. К тому же труд еще не завершен, многие аспекты теории сопротивления материалов еще не нашли отражения в моих статьях (и теперь вряд ли найдут, так как сил и желания на продолжение работы у меня уже нет).

Да я вроде целую статью посвятил объяснению осевых моментов инерции и добавить мне тут особенно нечего. Пожалуйста, перечитайте данную статью более внимательно и физический смысл вам откроется. Если нет, то обращайтесь.

Подскажите, где я ошибаюсь?

Примечание: Возможно ваш вопрос, особенно если он касается расчета конструкций, так и не появится в общем списке или останется без ответа, даже если вы задатите его 20 раз подряд. Почему, достаточно подробно объясняется в статье «Записаться на прием к доктору» (ссылка в шапке сайта).

Источник