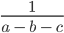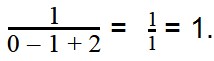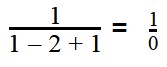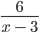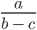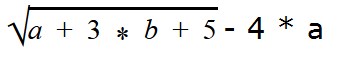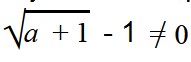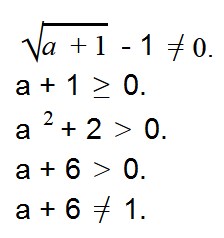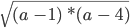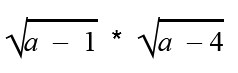Выражение имеет смысл что это значит
Числовые и алгебраические выражения. Преобразование выражений.
Что такое выражение в математике? Зачем нужны преобразования выражений?
Допустим, перед вами злой пример. Очень большой и очень сложный. Допустим, вы сильны в математике и ничего не боитесь! Сможете сразу дать ответ?
Вам придётся решать этот пример. Последовательно, шаг за шагом, этот пример упрощать. По определённым правилам, естественно. Т.е. делать преобразование выражений. Насколько успешно вы проведёте эти преобразования, настолько вы и сильны в математике. Если вы не умеете делать правильные преобразования, в математике вы не сможете сделать ни-че-го.
Во избежание такого неуютного будущего (или настоящего. ), не мешает разобраться в этой теме.)
Для начала выясним, что такое выражение в математике. Что такое числовое выражение и что такое алгебраическое выражение.
Что такое выражение в математике?
В общем виде термин «математическое выражение» применяется, чаще всего, чтобы не мычать. Спросят вас, что такое обыкновенная дробь, например? И как ответить?!
Первый вариант ответа: «Это. м-м-м-м. такая штука. в которой. А можно я лучше напишу дробь? Вам какую?»
Второй вариант как-то посолидней будет, правда?)
Вот в этих целях фраза «математическое выражение» очень хороша. И правильно, и солидно. Но для практического применения надо хорошо разбираться в конкретных видах выражений в математике.
Числовые выражения.
Что такое числовое выражение? Это очень простое понятие. Само название намекает, что это выражение с числами. Да, так оно и есть. Математическое выражение, составленное из чисел, скобок и знаков арифметических действий называется числовым выражением.
тоже числовое выражение, да.
Когда числовое выражение не имеет смысла?
Понятное дело, если мы видим перед собой какую-то абракадабру, типа
то делать ничего и не будем. Так как непонятно, что с этим делать. Бессмыслица какая-то. Разве что, посчитать количество плюсиков.
Но бывают внешне вполне благопристойные выражения. Например такое:
Чтобы дать такой ответ, пришлось, конечно, посчитать, что в скобочках будет. А иногда в скобочках такого понаворочено. Ну тут уж ничего не поделаешь.
Алгебраические выражения.
и так далее, до бесконечности. )
В арифметике можно записать, что
А вот если мы подобное равенство запишем через алгебраические выражения:
мы сразу решим все вопросы. Для всех чисел махом. Для всего бесконечного количества. Потому, что под буквами а и b подразумеваются все числа. И не только числа, но даже и другие математические выражения. Вот так работает алгебра.
Когда алгебраическое выражение не имеет смысла?
Про числовое выражение всё понятно. Там на ноль делить нельзя. А с буквами, разве можно узнать, на что делим?!
Возьмём для примера вот такое выражение с переменными:
Конечно. Просто в таких случаях говорят, что выражение
имеет смысл для любых значений а, кроме а = 5.
Весь набор чисел, которые можно подставлять в заданное выражение, называется областью допустимых значений этого выражения.
Как видите, ничего хитрого нет. Смотрим на выражение с переменными, да соображаем: при каком значении переменной получается запретная операция (деление на ноль)?
А потом обязательно смотрим на вопрос задания. Чего спрашивают-то?
Если спрашивают, при каком значении переменной выражение не имеет смысла, наше запретное значение и будет ответом.
Если спрашивают, при каком значении переменной выражение имеет смысл (почувствуйте разницу!), ответом будут все остальные числа, кроме запретного.
Зачем нам смысл выражения? Есть он, нет его. Какая разница?! Дело в том, что это понятие становится очень важным в старших классах. Крайне важным! Это основа для таких солидных понятий, как область допустимых значений или область определения функции. Без этого вы вообще не сможете решать серьёзные уравнения или неравенства. Вот так.
Преобразование выражений. Тождественные преобразования.
Мы познакомились с числовыми и алгебраическими выражениями. Поняли, что означает фраза «выражение не имеет смысла». Теперь надо разобраться, что такое преобразование выражений. Ответ прост, до безобразия.) Это любое действие с выражением. И всё. Вы эти преобразования делали с первого класса.
Возьмём крутое числовое выражение 3+5. Как его можно преобразовать? Да очень просто! Посчитать:
Вот этот расчёт и будет преобразованием выражения. Можно записать то же самое выражение по-другому:
Тут мы вообще ничего не считали. Просто записали выражение в другом виде. Это тоже будет преобразованием выражения. Можно записать вот так:
Любое действие над выражением, любая запись его в другом виде называется преобразованием выражения. И все дела. Всё очень просто. Но есть здесь одно очень важное правило. Настолько важное, что его смело можно назвать главным правилом всей математики. Нарушение этого правила неизбежно приводит к ошибкам. Вникаем?)
Предположим, мы преобразовали наше выражение как попало, вот так:
Преобразование? Конечно. Мы же записали выражение в другом виде, что здесь не так?
Всё не так.) Дело в том, что преобразования «как попало» математику не интересуют вообще.) Вся математика построена на преобразованиях, в которых меняется внешний вид, но суть выражения не меняется. Три плюс пять можно записать в каком угодно виде, но это должно быть восемь.
Преобразования, не меняющие сути выражения называются тождественными.
Именно тождественные преобразования и позволяют нам, шаг за шагом, превращать сложный пример в простое выражение, сохраняя суть примера. Если в цепочке преобразований мы ошибёмся, сделаем НЕ тождественное преобразование, дальше мы будем решать уже другой пример. С другими ответами, которые не имеют отношения к правильным.)
Вот оно и главное правило решения любых заданий: соблюдение тождественности преобразований.
Пример с числовыми выражением 3+5 я привёл для наглядности. В алгебраических выражениях тождественные преобразования даются формулами и правилами. Скажем, в алгебре есть формула:
Как вы, наверняка, догадались, эту цепочку можно продолжать до бесконечности. ) Очень важное свойство. Именно оно позволяет превращать всякие монстры-примеры в белые и пушистые.)
Если Вам нравится этот сайт.
Кстати, у меня есть ещё парочка интересных сайтов для Вас.)
А вот здесь можно познакомиться с функциями и производными.
Область допустимых значений функции
Статья находится на проверке у методистов Skysmart.
Если вы заметили ошибку, сообщите об этом в онлайн-чат (в правом нижнем углу экрана).
Допустимые и недопустимые значения переменных
В 7 классе заканчивается математика и начинается ее-величество-алгебра. Первым делом школьники изучают выражения с переменными.
Мы уже знаем, что математика состоит из выражений — буквенных и числовых. Каждому выражению, в котором есть переменная, соответствует область допустимых значений (ОДЗ). Если игнорировать ОДЗ, то в результате решения можно получить неверный ответ. Получается, чтобы быстро получить верный ответ, нужно всегда учитывать область допустимых значений.
Чтобы дать верное определение области допустимых значений, разберемся, что такое допустимые и недопустимые значения переменной.
Рассмотрим все необходимые определения, связанные с допустимыми и недопустимыми значениями переменной.
Выражение с переменными — это буквенное выражение, в котором буквы обозначают величины, принимающие различные значения.
Значение числового выражения — это число, которое получается после выполнения всех действий в числовом выражении.
Выражение с переменными имеет смысл при данных значениях переменных, если при этих значениях переменных можно вычислить его значение.
Выражение с переменными не имеет смысла при данных значениях переменных, если при этих значениях переменных нельзя вычислить его значение.
Теперь, опираясь на данные определения, мы можем сформулировать, что такое допустимые и недопустимые значения переменной.
Допустимые значения переменных — это значения переменных, при которых выражение имеет смысл.
Если при переменных выражение не имеет смысла, то значения таких переменных называют недопустимыми.
В выражении может быть больше одной переменной, поэтому допустимых и недопустимых значений может быть больше одного.
Пример 1
Рассмотрим выражение
В выражении три переменные (a, b, c).
Запишем значения переменных в виде: a = 1, b = 1, c = 2.
Такие значения переменных являются допустимыми, поскольку при подстановке этих значений в выражение, мы легко можем найти ответ:
Таким же образом можем выяснить, какие значения переменных — недопустимые.
Подставим значения переменных в выражение
На ноль делить нельзя.
Что такое ОДЗ
ОДЗ — это невидимый инструмент при решении любого выражении с переменной. Чаще всего, ОДЗ не отображают графически, но всегда «держат в уме».
Область допустимых значений (ОДЗ) — это множество всех допустимых значений переменных для данного выражения.
Пример 2
Рассмотрим выражение
Пример 3
Рассмотрим выражение
ОДЗ такого выражения будет выглядеть вот так: b ≠ c; a — любое число.
Такая запись означает, что область допустимых значений переменных b, c и a = это все значения переменных, при которых соблюдаются условия b ≠ c; a — любое число.
Как найти ОДЗ: примеры решения
Найти ОДЗ — это значит, что нужно указать все допустимые значения переменных для выражения. Часто, чтобы найти ОДЗ, нужно выполнить преобразование выражения.
Чтобы быстро и верно определять ОДЗ, запомните условия, при которых значение выражения не может быть найдено.
Мы не можем вычислить значение выражения, если:
Теперь, приступая к поиску ОДЗ, вы можете сверять выражение по всем этим пунктам.
Давайте потренируемся находить ОДЗ.
Пример 4
Найдем область допустимых значений переменной выражения a 3 + 4 * a * b − 6.
В куб возводится любое число. Ограничений при вычитании и сложении нет. Это значит, что мы можем вычислить значение выражения a 3 + 4 * a * b − 6 при любых значениях переменной.
ОДЗ переменных a и b — это множество таких пар допустимых значений (a, b), где a — любое число и b — любое число.
Ответ: (a и b), где a — любое число и b — любое число.
Пример 5
Найдем область допустимых значений (ОДЗ) переменной выражения
Здесь нужно обратить внимание на наличие нуля в знаменатели дроби. Одним из условий, при котором вычисление значения выражения невозможно явлется наличие деления на ноль.
Это значит, что мы может сказать, что ОДЗ переменной a в выражении 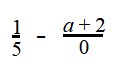
Пустое множество изображается в виде вот такого символа Ø.
Пример 6
Найдем область допустимых значений (ОДЗ) переменных в выражении
Если есть квадратный корень, то нам нужно следить за тем, чтобы под знаком корня не было отрицательного числа. Это значит, что при подстановке значений a и b должны быть условия, при которых a + 3 * b + 5 ≥ 0.
Ответ: ОДЗ переменных a и b — это множество всех пар, при которых a + 3 * b + 5 ≥ 0.
Пример 7
Найдем ОДЗ переменной a в выражении
Прежде всего, нам нужно подобрать такое условие, при котором в знаменателе дроби не будет ноля —
Мы знаем, что выражение под знаком корня должно быть положительным. Это дает нам второе условие: a + 1 ≥ 0.
Мы не можем вычислить логарифм отрицательного выражения. Получаем третье условие: a 2 + 2 > 0.
Выражении в основании логарифма не должно быть отрицательным и не должно равняться единице. Получаем условие 4: a + 6 > 0.
Как видите, записывая ОДЗ, мы ставим квадратные и круглые скобки.
Запомните
Например, если х > 6, но х
Зачем учитывать ОДЗ при преобразовании выражения
Иногда выражение просто невозможно решить, если не выполнить ряд тождественных преобразований. К ним относятся: перестановки, раскрытие скобок, группировка, вынесение общего множителя за скобки, приведение подобных слагаемых.
Кроме того, что видов таких преобразований довольно много: нужно понимать, в каких случаях какое преобразование возможно. В этом может помочь определение ОДЗ.
Тождественное преобразование может:
Рассмотрим каждый случай в отдельности.
Пример 8
Поскольку мы должны следить за тем, чтобы в выражении не возникало деление ноль, определяем условие a ≠ 0.
Это условие отвечает множеству (−∞ ; 0) ∪ (0 ; +∞).
В выражении есть подобные слагаемые, если привести подобные слагаемые, то мы получаем выражение вида a.
ОДЗ для a — это R — множество всех вещественных чисел.
Преобразование расширило ОДЗ — добавился ноль.
Пример 9
Рассмотрим выражение a 2 + a + 4 * a
ОДЗ a для этого выражения — множество R.
В выражении есть подобные слагаемые, выполним тождественное преобразование.
После приведения подобных слагаемых выражение приняло вид a 2 + 5 * a
ОДЗ переменной a для этого выражения — множество R.
Это значит, что тождественное преобразование никак не повлияло на ОДЗ.
Пример 10
Рассмотрим выражение
Решить такое неравенство можно методом интервалов, что дает нам ОДЗ (−∞; 1] ∪ [4 ; +∞).
Затем выполним преобразование исходного выражения по свойству корней: корень произведения = произведению корней.
Приведем выражение к виду
Решив систему линейных неравенств, получаем множество [4; + ∞).
Отсюда видно, что тождественные преобразования сузили ОДЗ.
От (−∞; 1] ∪ [4 ; +∞) до [4; + ∞).
Решив преобразовать выражение, внимательно следите за тем, чтобы не допустить сужение ОДЗ.
Запомните, что выполняя преобразование, следует выбирать такие, которые не изменят ОДЗ.
Выражение, не имеющее смысла: примеры в математике
Выражение – это самый широкий математический термин. По существу, в этой науке из них состоит все, и все операции проводятся тоже над ними. Другой вопрос, что в зависимости от конкретного вида применяются совершенно разнообразные методы и приемы. Так, работа с тригонометрией, дробями или логарифмами – это три различных действия. Выражение, не имеющее смысла, может относится к одному из двух видов: числовому или алгебраическому. А вот что означает это понятие, как выглядит его пример и прочие моменты будут рассмотрены далее.
Числовые выражения
Если выражение состоит из чисел, скобок, плюсов-минусов и остальных знаков арифметических действий, его смело можно называть числовым. Что довольно логично: стоит только еще разок взглянуть на первый названный его компонент.
Числовым выражением может быть что угодно: главное, чтобы в нем не было букв. А под «чем угодно» в данном случае понимается все: от простой, стоящей одиноко, самой по себе, цифры, до огромного их перечня и знаков арифметических действий, требующих последующего вычисления конечного результата. Дробь – это тоже числовое выражение, если в ней нет всяких a, b, c, d и т.д., ведь тогда это совершенно другой вид, о котором будет рассказано чуть позже.
Условия для выражения, которое не имеет смысла
Когда задание начинается со слова «вычислить», можно говорить о преобразовании. Штука в том, что это действие не всегда целесообразно: в нем не то чтобы сильно нуждаются, если на передний план выходит выражение, не имеющее смысла. Примеры бесконечно удивительны: иногда, чтобы понять, что оно-то нас и настигло, приходится долго и нудно раскрывать скобки и считать-считать-считать.
Главное, что нужно запомнить: не имеет смысла то выражения, чей конечный результат сводится к запретному в математике действию. Если уж совсем по-честному, то тогда бессмысленным становится само преобразование, но для того, чтобы это выяснить, приходится его для начала выполнить. Такой вот парадокс!
Самое знаменитое, но от того не менее важное запретное математическое действие – это деление на ноль.
Потому вот, например, выражение, не имеющее смысла:
Если при помощи нехитрых вычислений свести вторую скобку к одной цифре, то она и будет нулем.
По такому же принципу «почетное звание» дается и этому выражению:
Алгебраические выражения
Это то же самое числовое выражение, если в него добавить запретные буквы. Тогда оно и становится полноценным алгебраическим. Оно также может быть всех размеров и форм. Алгебраическое выражение – понятие более широкое, включающее в себя предыдущее. Но был смысл начинать разговор не с него, а с числового, чтобы было понятнее и разобраться было легче. Ведь имеет ли смысл выражение алгебраическое – вопрос не то чтобы очень сложный, но имеющий больше уточнений.
Почему так?
Буквенное выражение, или выражение с переменными – это синонимы. Первый термин объяснить просто: ведь оно, в конце концов, содержит в себе буквы! Второй тоже не загадка века: вместо букв можно подставлять разные числа, вследствие чего значение выражения будет меняться. Нетрудно догадаться, что буквы в данном случае и есть переменные. По аналогии, числа – это постоянные.
И тут мы возвращаемся к основной тематике: что такое выражение, не имеющее смысла?
Примеры алгебраических выражений, не имеющих смысла
А вот насчет (a+3):(12-4-8) можно смело сказать, что это выражение, не имеющее смысла при любых a.
Типовые задачи по теме «Выражение, не имеющее смысла»
7 класс изучает эту тему по математике в числе прочих, и задания по ней встречаются нередко как непосредственно после соответствующего занятия, так и в качестве вопроса «с подвохом» на модулях и экзаменах.
Вот почему стоит рассмотреть типовые задачи и методы их решения.
Имеет ли смысл выражение:
Необходимо произвести все вычисление в скобках и привести выражение к виду:
Конечный результат содержит деление на ноль, следовательно, выражение не имеет смысла.
Какие выражения не имеют смысла?
Следует вычислить конечное значение для каждого из выражений.
Найти область допустимых значений для следующих выражений:
То есть задание звучит как: найти значения, при которых не будет деления на ноль.
Но на самом деле оно только выглядит страшным и громоздким, потому что на деле содержит в себе то, что уже давно известно: возведение чисел в квадрат и куб, некоторые арифметические действия, такие как деление, умножение, вычитание и сложения. Для удобства, между прочим, можно привести задачу к дробному виду.
Записываем ответ: 3 и 5.
В заключение
Как видно, эта тема очень интересная и не особо сложная. Разобраться в ней не составит труда. Но все-таки отработать пару примеров никогда не помешает!
имеет смысл
Полезное
Смотреть что такое «имеет смысл» в других словарях:
Смысл — Смысл ♦ Sens Значение (слова, предложения и т. д.). Иметь смысл – значит желать что то сказать или сделать. Это желание (воление) может быть явным или скрытым, сознательным или неосознанным, оно может даже казаться лишь видимостью желания,… … Философский словарь Спонвиля
смысл — сущ., м., употр. очень часто Морфология: (нет) чего? смысла, чему? смыслу, (вижу) что? смысл, чем? смыслом, о чём? о смысле; мн. что? смыслы, (нет) чего? смыслов, чему? смыслам, (вижу) что? смыслы, чем? смыслами, о чём? о смыслах 1. Смыслом… … Толковый словарь Дмитриева
Смысл жизни — Возможно, эта статья содержит оригинальное исследование. Добавьте ссылки на источники, в противном случае она может быть выставлена на удаление. Дополнительные сведения могут быть на странице обсуждения. (25 мая 2011) … Википедия
СМЫСЛ ИСТОРИИ — одно из ключевых понятий философии истории, характеризующее ту цель, которая стоит перед человечеством и которую оно стремится реализовать в ходе своей постепенной эволюции. Цель как истории, так и любой человеческой деятельности представляет… … Философская энциклопедия
Смысл любви (Соловьёв) — Смысл любви цикл из пяти статей Владимира Соловьева, опубликованный в журналах 1892 1893 годах. Н. А. Бердяев считал, что « Смысл любви Вл. Соловьева самое замечательное, что было написано о любви»[1]. Как пишет А.Ф.Лосев в своей… … Википедия
Смысл — Смысл сущность феномена в более широком контексте реальности. Смысл феномена оправдывает существование феномена, так как определяет его место в некоторой целостности, вводит отношения «часть целое», делает его необходимым в качестве части… … Википедия
СМЫСЛ ЖИЗНИ — Стоит ли жизнь того, чтобы жить? Это вопрос для эмбриона, не для мужчины. Сэмюэл Джонсон Жизнь, быть может, не стоит того, чтобы жить, но что с ней еще можно делать? Есть ли смысл жизни? Смотря когда. Давид Самойлов Жизнь имеет в точности ту… … Сводная энциклопедия афоризмов
смысл — СМЫСЛ (англ. sense, meaning; нем. Sinn, Bedeutung) понятие, обозначающее отнесенность знака, явления, события к человеку или некоторому высшему существу (широкое употребление); понятие, характеризующее содержание языковых выражений (узкое … Энциклопедия эпистемологии и философии науки
СМЫСЛ — способ представления денотата в знаке (см. ЗНАК) (определение Готтлоба Фреге). Это означает, в частности, что у знака может быть несколько С. при одном денотате, то есть том предмете, который этим знаком обозначается. Например, имя Аристотель… … Энциклопедия культурологии
СМЫСЛ ЖИЗНИ ЧЕЛОВЕКА — эйдос индивида, умопостигаемая целостность всех проявлений его души. Стихия С.Ж. не материя и не энергия, а информация. Догадка о чьем либо С. ж. (в т. ч. о собственном) есть попытка понять скрытую форму правления души в теле, заключить о… … Современный философский словарь