Выпуклый многоугольник что это
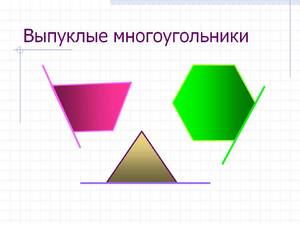
Выпуклый многоугольник
Что такое выпуклый многоугольник? В чём отличие выпуклого многоугольника от многоугольника, который не является выпуклым?
Выпуклый многоугольник — это многоугольник, лежащий в одной полуплоскости от каждой прямой, содержащей его сторону.
То есть ни одна из прямых, проходящих через две соседние вершины выпуклого многоугольника, не разрезает этот многоугольник на две части.
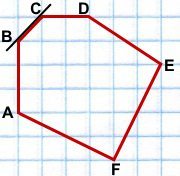
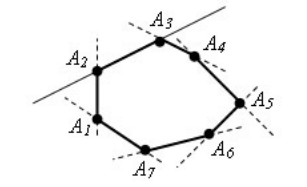
1) ABCDEF — выпуклый шестиугольник, так как он лежит в одной полуплоскости относительно каждой из прямых AB, BC, CD, DE и EF.
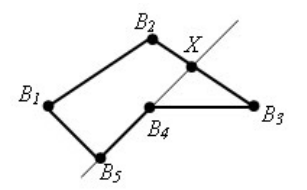
2) MNKFEL — не выпуклый шестиугольник,
Он не лежит в одной полуплоскости относительно прямых KF и FE.
Не выпуклый многоугольник можно разбить на конечное число выпуклых многоугольников. Поэтому в курсе геометрии средней школы изучают только выпуклые многоугольники.
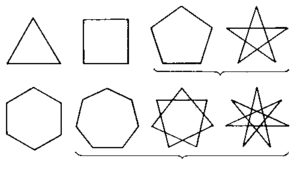
Важнейшие виды выпуклых многоугольников
Какой многоугольник называется выпуклым
Что такое выпуклый многогольник
Выпуклым называют многоугольник, все точки которого лежат по одну сторону от любой прямой, проходящий через две его соседние вершины.
Или же другой вариант определения:
Выпуклым называют многоугольник, в котором соблюдается следующее условие: если выбрать две произвольных точки, лежащих внутри фигуры, и соединить их отрезком, то все точки этого отрезка так же будут лежать внутри многоугольника.
Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.
Примеры
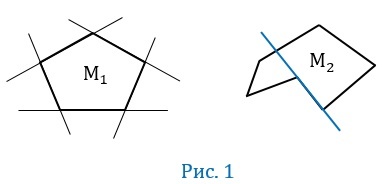
Многоугольник \(М_1\) — выпуклый, а \(М_2\) — не выпуклый.
Сумма углов выпуклого многоугольника
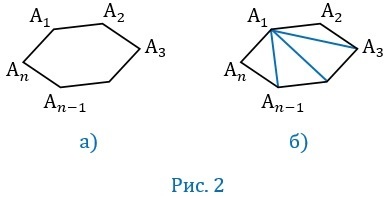
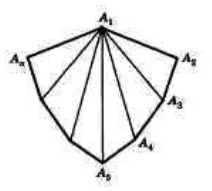
\(A_1A_2A_3. A_n\) — выпуклый многоугольник. Найдем сумму его углов:
\(\angle A_nA_1A_2,\;\angle A_1A_2A_3,\;\angle A_
Сумма внешних углов выпуклого многоугольника
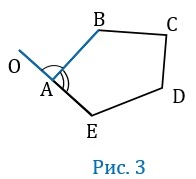
\(\angle OAD\) — внешний угол многоугольника ABCDE при вершине А. (смежный с \(\angle BAE\) )
\(180^\circ-A_1+180^\circ-A_2+. +180^\circ-A_n=n\cdot180^\circ-(A_1+A_2+. +A_n)=n\cdot180^\circ-(n-2)\cdot180^\circ=n\cdot180^\circ-n\cdot180^\circ+2\cdot180^\circ=360^\circ\)
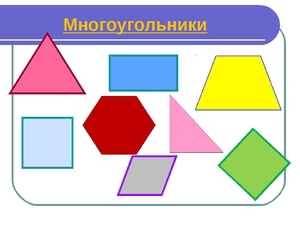
Геометрическая фигура многоугольник
Многоугольником называется геометрическая фигура, которая со всех сторон ограничена замкнутой ломаной линией. При этом количество звеньев ломаной не должно быть меньше трех. Каждая пара отрезков ломаной имеет общую точку и образует углы. Количество углов совместно с количеством отрезков ломаной являются основными характеристиками многоугольника. В каждом многоугольнике количество звеньев ограничивающей замкнутой ломаной совпадает с количеством углов.
Сторонами в геометрии принято называть звенья ломаной линии, которая ограничивает геометрический объект. Вершинами называют точки соприкосновения двух соседних сторон, по количеству которых получают свои названия многоугольники.
Если замкнутая ломаная состоит из трех отрезков, она носит название треугольника; соответственно, из четырех отрезков — четырехугольником, из пяти — пятиугольником и пр.
Для обозначения треугольника или четырехугольника пользуются заглавными латинскими буквами, обозначающими его вершины. Буквы называют по порядку — по часовой стрелке или против нее.
Основные понятия
Описывая определение многоугольника, следует учитывать некоторые смежные геометрические понятия:
Как уже упоминалось выше, названия многоугольных геометрических строятся исходя из количества вершин. Если у фигуры их количество равняется n, она носит название n-угольника:
Любой выпуклый n-угольник можно поделить на треугольники. При этом количество треугольников бывает меньше количества сторон на 2.
Виды фигур
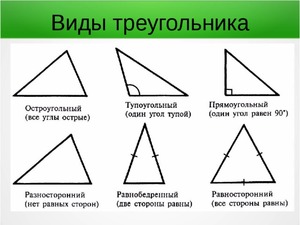
Треугольник
Это многоугольник с тремя вершинами и тремя отрезками, соединяющими их. При этом точки соединения отрезков не лежат на одной прямой.
Точки соединения отрезков — это вершины треугольника. Сами отрезки называются сторонами треугольника. Общая сумма внутренних углов каждого треугольника равняется 180°.
По соотношениям между сторонами все треугольники можно подразделять на несколько видов:
Кроме того, принято различать следующие треугольники:
Четырехугольник
Четырехугольником называется плоская фигура, имеющая 4 вершины и 4 отрезка, которые их последовательно соединяют.
На одной прямой не может находиться сразу три вершины четырехугольника.
Видео
Дополнительную информацию о многоугольниках вы найдете в этом видео.
» width=»560″ height=»314″ allowfullscreen=»allowfullscreen»>Что такое выпуклый и невыпуклый многоугольник
Выпуклым многоугольником называется многоугольник, все точки которого лежат по одну сторону от любой прямой, проходящей через две его соседние вершины.
Содержание
Определения [ править | править код ]
Существует множество эквивалентных определений:
Что такое выпуклый многоугольник? В чём отличие выпуклого многоугольника от многоугольника, который не является выпуклым?
Выпуклый многоугольник — это многоугольник, лежащий в одной полуплоскости от каждой прямой, содержащей его сторону.
То есть ни одна из прямых, проходящих через две соседние вершины выпуклого многоугольника, не разрезает этот многоугольник на две части.
1) ABCDEF — выпуклый шестиугольник, так как он лежит в одной полуплоскости относительно каждой из прямых AB, BC, CD, DE и EF.
2) MNKFEL — не выпуклый шестиугольник,
Он не лежит в одной полуплоскости относительно прямых KF и FE.
Не выпуклый многоугольник можно разбить на конечное число выпуклых многоугольников. Поэтому в курсе геометрии средней школы изучают только выпуклые многоугольники.
Важнейшие виды выпуклых многоугольников
Прежде, чем ввести понятие многоугольника, рассмотрим геометрическую фигуру, состоящую из отрезков. Расположим отрезки так, чтобы начало одного отрезка совпадало с концом другого.
Таких отрезков может быть бесконечно много.
Определение. Ломаной называется геометрическая фигура, состоящая из последовательно соединённых отрезков, в которой конец одного отрезка является началом следующего. При этом соседние (имеющие общую точку) отрезки не должны лежать на одной прямой.
Определение. Длиной ломаной называется сумма длин всех её звеньев.
На рисунке длина ломаной равна:
Существует две группы ломаных: замкнутые и незамкнутые.
Определение. Замкнутой называется ломаная, у которой её начало и конец совпадают.
– замкнутая ломаная. У неё точка является и началом и концом.
Замкнутые ломаные также разделяются на две группы:
ломаные без самопересечения (когда несоседние звенья не пересекаются);
ломаные, имеющие самопересечение (когда несоседние звенья пересекаются).
Определение. Многоугольником называется замкнутая ломаная, не имеющая самопересечений.
Определение. Диагональю многоугольника называется отрезок, соединяющий две несоседние вершины.
Любой многоугольник разделяет плоскость на две области: внутреннюю и внешнюю.
Рассмотрим два вида многоугольников.
Визуально видно, что в них есть принципиальная разница. В чём она? Приложите линейку к любой стороне красного многоугольника. Вы заметили, что весь многоугольник находится по одну сторону от линейки. Попробуйте это сделать со всеми остальными сторонами. Многоугольник всё также расположен по одну сторону от линейки.
Теперь перейдём к зелёному многоугольнику и проделаем то же самое: приложим линейку к каждой стороне. Тут вы должны заметить, что существуют две стороны, к которым прикладываем линейку и многоугольник делится на две части. В этом и есть принципиальная разница между этими двумя многоугольниками.
Определение. Выпуклым называется многоугольник, все точки которого лежат по одну сторону от любой прямой, проходящей через две его соседние вершины.
Выпуклый многоугольник можно ещё определить так: это многоугольник, все диагонали которого лежат внутри многоугольника. Если в зелёном многоугольнике провести диагональ через две верхние вершины, то она окажется за пределами самого многоугольника. Поэтому, зелёный многоугольник не является выпуклым. Он называется невыпуклым.
Любой выпуклый многоугольник (кроме треугольника) можно разделить на треугольники его диагоналями. Выясним на примере нескольких многоугольников, сколько можно провести диагоналей из каждой вершины, и сколько получается треугольников.
Многоугольник, выпуклый многоугольник, четырехугольник
Вы будете перенаправлены на Автор24
Понятие многоугольника
Многоугольником называется геометрическая фигура в плоскости, которая состоит из попарно соединенных между собой отрезков, соседние из которых не лежат на одной прямой.
Виды многоугольников
Если многоугольник всегда будет лежать по одну сторону от любой прямой, проходящей через его стороны, то многоугольник называется выпуклым (рис. 1).
Рисунок 1. Выпуклый многоугольник
Если многоугольник лежит по разные стороны хотя бы одной прямой, проходящей через его стороны, то многоугольник называется невыпуклым (рис. 2).
Рисунок 2. Невыпуклый многоугольник
Сумма углов многоугольника
Доказательство.
Теорема доказана.
Готовые работы на аналогичную тему
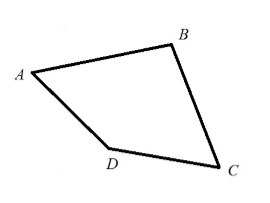
Понятие четырехугольника
Рисунок 4. Четырехугольник
Для четырехугольника аналогично определены понятия выпуклого четырехугольника и невыпуклого четырехугольника. Классическими примерами выпуклых четырехугольников являются квадрат, прямоугольник, трапеция, ромб, параллелограмм (рис. 5).
Рисунок 5. Выпуклые четырехугольники
Доказательство.
Следовательно, сумма углов выпуклого четырехугольника равняется
Теорема доказана.
Примеры задач
Определить сумму углов выпуклого девятиугольника, семиугольника и двенадцатиугольника.
Решение.
Сумма углов выпуклого пятиугольника равняется
Сумма углов выпуклого девятиугольника равняется
Сумма углов выпуклого двенадцатиугольника равняется
Решение.
Получи деньги за свои студенческие работы
Курсовые, рефераты или другие работы
Автор этой статьи Дата последнего обновления статьи: 12 05 2021