Вы точно знаете что в кодовом слове пять 0 и десять 1
5. Кодирование и декодирование
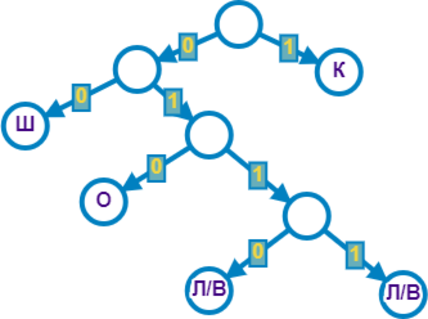
Для кодирования последовательности, состоящей из букв слова ШKOЛKOВО решили использовать неравномерный двоичный код, удовлетворяющий условию Фано. Для буквы Ш использовали кодовое слово 00, для буквы К — 1. Укажите, какова наименьшая длина всех символов заданного слова.
Построим дерево для решения задачи. Для букв Ш и К есть кодовые слова 00 и 1 соответственно. В слове ШКОЛКОВО самая частовстречаемая буква — О, следовательно, её нужно закодировать минимальновозможным количеством символов.
Минимально возможная длина кодового слова для буквы состоит из трёх битов, то есть О закодируем с помощью 010.
Буквы Л и В встречаются всего один раз, закодируем их минимально возможным количеством символов.
Самая маленькая длина кодовых слов для них \(=4\) : 0110 и 0111.
Посчитаем сумму длин кодовых слов:
Ш, Л и В встречаются один раз,
Для кодирования последовательности, состоящей из букв слова Р, Б, О, Т, А используется неравномерный двоичный код, удовлетворяющий прямому условию Фано.
Вот этот код: А – 0; Р – 100; Б – 1010; О – 111; Т – 110. Необходимо сократить для одной из букв длину кодового слова так, чтобы код можно было однозначно декодировать.
Для какой буквы это возможно сделать? В ответе укажите эту букву.
Так как код удовлетворяет прямому условию Фано (ни одно кодовое слово не является началом другого), то следует учитывать это при сокращении исходных кодовых слов.
1. Код буквы А сократить нельзя, так как он состоит всего из одного символа.
2. Р сократить нельзя,так как при сокращении до 10 код перестанет удовлетворять прямому условию Фано.
3. Б возможно сократить до 101, в таком случае код по-прежнему будет удовлетворять одному из условий Фано (прямому).
4. О нельзя сократить, т.к. в этом случае нарушится прямое условие Фано.
5. Код буквы Т нельзя сократить, т.к тогда он совпадёт с началом кода буквы О, что недопустимо при выполнении прямого условия Фано.
По каналу связи передаются сообщения, которые содержат только следующие буквы: С, Т, Р, И, М; для передачи используется двоичный код, удовлетворяющий условию Фано. Для букв С, Т, Р используются такие кодовые слова: С – 0; Т – 110; Р – 101. Укажите кратчайшее кодовое слово для буквы И, при котором код будет допускать однозначную расшифровку. Если таких кодов несколько, укажите код с наименьшим числовым значением.
Построим дерево решений. Код не может начинаться с нуля, т.к из данной вершины нельзя построить новые варианты, удовлетворяющие условию Фано. Из схемы видно, что для букв И, М есть два возможных варианта кодировки,которые начинаются с 1.
Первый вариант: 111
Второй вариант: 100
Оба варианта удовлетворяют условию Фано (не являются началом других кодовых слов), нам подходит вариант с наименьшим значением, то есть 100 — ответ.
Разряды и классы чисел
Статья находится на проверке у методистов Skysmart.
Если вы заметили ошибку, сообщите об этом в онлайн-чат
(в правом нижнем углу экрана).
Числа и цифры
Числа — это единицы счета. С помощью чисел можно сосчитать количество предметов и определить различные величины.
Для записи чисел используются специальные знаки — цифры. Всего их десять: 1, 2, 3, 4, 5, 6, 7, 8, 9, 0.
Натуральные числа — это числа, которые мы используем при счете. Вот они: 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18, 19, 20, …
От количества цифр в числе зависит его название.
Число, которое состоит из одного знака, называется однозначным. Наименьшее однозначное — 1, наибольшее — 9.
Число, которое состоит из двух знаков цифр, называется двузначным. Наименьшее двузначное — 10, наибольшее — 99.
Числа, которые записаны с помощью двух, трех, четырех и более цифр, называются двузначными, трехзначными, четырехзначными или многозначными. Наименьшее трехзначное — 100, наибольшее — 999.
Каждая цифра в записи многозначного числа занимает определенное место — позицию.
Классы чисел
Цифры в записи многозначных чисел разбивают справа налево на группы по три цифры в каждой. Эти группы называют классами. В каждом классе цифры справа налево обозначают единицы, десятки и сотни этого класса.
Названия классов многозначных чисел справа налево:
Чтобы читать запись многозначного числа было удобно, между классами оставляют небольшой пробел. Например, чтобы прочитать число 125911723296, удобно сначала выделить в нем классы:
А теперь прочитаем число единиц каждого класса слева направо:
Разряды чисел
От позиции, на которой стоит цифра в записи числа, зависит ее значение. Например:
Можно сформулировать иначе и сказать, что в заданном числе 1 123 цифра 3 располагается в разряде единиц, 2 в разряде десятков, 1 в разряде сотен, а 1 служит значением разряда тысяч.
Проясним, что такое разряд в математике. Разряд — это позиция или место расположения цифры в записи натурального числа.
У каждого разряда есть свое название. Слева всегда живут старшие разряды, а справа — младшие. Чтобы быстрее запомнить, можно использовать таблицу.
Количество разрядов всегда соответствует количеству знаков в числе. В этой таблице есть названия всех разрядов для числа, которое состоит из 15 знаков. У следующих разрядов также есть названия, но они используются крайне редко.
Низший (младший) разряд многозначного натурального числа — разряд единиц.
Высший (старший) разряд многозначного натурального числа — разряд, соответствующий крайней левой цифре в заданном числе.
Вы наверняка заметили, что в учебниках часто ставят небольшие пробелы при записи многозначных чисел. Так делают, чтобы натуральные числа было удобно читать. А еще чтобы визуально разделить классы чисел.
Разрядные единицы обозначают так:
Каждые три разряда, следующие друг за другом, составляют класс. Первые три разряда: единицы десятки и сотни — образуют класс единиц (первый класс). Следующие три разряда: единицы тысяч, десятки тысяч и сотни тысяч — образуют класс тысяч (второй класс). Третий класс будут составлять единицы, десятки и тысячи миллионов и так далее.
Чтобы легче понимать математику — записывайтесь на наши курсы по математике!
Потренируемся
Пример 1. Записать цифрами число, в котором содержится:
Все разрядные единицы, кроме простых единиц, называют составными единицами. Каждые десять единиц любого разряда составляют одну единицу следующего более высокого разряда:
Чтобы узнать, сколько в числе заключается всех единиц какого-либо разряда, нужно отбросить все цифры, обозначающие единицы низших разрядов и прочитать число, которое выражено оставшимися цифрами.
Пример 2. Сколько сотен содержится в числе 6284?
В числе 6284 на третьем месте в классе единиц стоит цифра 2, значит, в числе есть две сотни.
Следующая цифра слева — 6, означает тысячи. Так как в каждой тысяче содержится 10 сотен то, в 6 тысячах их заключается 60.
Значит, в данном числе содержится 62 сотни.
Цифра 0 в любом разряде означает отсутствие единиц в данном разряде.
Проще говоря, цифра 0 в разряде десятков означает отсутствие десятков, в разряде сотен — отсутствие сотен и т. д. В том разряде, где стоит 0, при чтении числа ничего не произносится:
Чтобы проще освоить эту тему, можно распечатать таблицу классов и разрядов для учащихся 4 класса и обращаться к ней, если возникнут сложности.
Вы точно знаете что в кодовом слове пять 0 и десять 1
Для передачи сообщений, содержащих только буквы К, Л, М, Н, О, П, Р, решили использовать неравномерный двоичный код, в котором никакое кодовое слово не является началом другого кодового слова. Это условие обеспечивает возможность однозначной расшифровки закодированных сообщений. Известны кодовые слова, использованные для некоторых букв: К — 11, Л — 000, П — 0010, Р — 1011.
Какое кодовое слово надо назначить для буквы М, чтобы код удовлетворял указанному условию и при этом длина слова МОЛОКО после кодирования была наименьшей? Если таких кодов несколько, укажите код с наименьшим числовым значением.
Буква О повторяется в слове МОЛОКО три раза, поэтому закодируем букву О кодом 01. Букву М можем закодировать кодовым словом 100, условие Фано не нарушено. Таким образом, ответ — 100.
Для кодирования некоторой последовательности, состоящей из букв А, Б, В, Г, Д, Е, решили использовать неравномерный двоичный код, удовлетворяющий условию Фано. Для буквы А использовали кодовое слово 0; для буквы Б – кодовое слово 10. Какова наименьшая возможная сумма длин всех шести кодовых слов?
Примечание. Условие Фано означает, что никакое кодовое слово не является началом другого кодового слова. Это обеспечивает возможность однозначной расшифровки закодированных сообщений.
Для нахождения кодовых слов будем использовать двоичное дерево, в котором от каждого узла отходит две ветви, соответствующие выбору следующей цифры кода. Буквы будем размещать на конечных узлах дерева — листьях. Условие Фано выполняется, поскольку при проходе от корня дерева к букве в середине пути не встречается других букв.
Пример дерева, обеспечивающего минимальную сумму длин всех шести кодов изображено на рисунке.
Суммарная длина такого кода 1 + 2 + 4 + 4 + 4 + 4 = 19.
Для кодирования некоторой последовательности, состоящей из букв А, Б, В, Г, Д, Е, решили использовать неравномерный двоичный код, удовлетворяющий условию Фано. Для букв А, Б, В, Г использовали соответственно кодовые слова 000, 001, 10, 11. Укажите кратчайшее возможное кодовое слово для буквы Д, при котором код будет допускать однозначное декодирование. Если таких кодов несколько, укажите код с наименьшим числовым значением. Примечание. Условие Фано означает, что никакое кодовое слово не является началом другого кодового слова. Это обеспечивает возможность однозначной расшифровки закодированных сообщений.
Однозначные коды не подходят по условию Фано. Кратчайшее подходящее кодовое слово — 01. Но выбирая его, не останется вариантов закодировать букву E, значит, нужно взять минимум трехзначный код. Минимальный из них, подходящий по условию Фано — 010. Тогда букву Е можно закодировать как 011.
Для кодирования некоторой последовательности, состоящей из букв А, Б, В, Г, Д, Е, решили использовать неравномерный двоичный код, удовлетворяющий условию Фано. Для букв А, Б, В, Г использовали соответственно кодовые слова 000, 001, 10, 11. Укажите кратчайшее возможное кодовое слово для буквы Д, при котором код будет допускать однозначное декодирование. Если таких кодов несколько, укажите код с наименьшим числовым значением. Примечание. Условие Фано означает, что никакое кодовое слово не является началом другого кодового слова. Это обеспечивает возможность однозначной расшифровки закодированных сообщений.
Поскольку все однозначные и двузначные слова не подходят по условию Фано, нужно найти трехзначное слово, которое было бы максимально и удовлетряло условию. Так как 111, 101 и 110 нарушают условие Фано, то искомое слово — 010.
Заметим, что двузначное кодовое слово 01 не подходит, поскольку при его использовании нельзя подобрать кодовое слово для буквы Е.
Дублирует задание 13481.
Для кодирования сообщения, состоящего только из букв А, Б, В и Г, используется неравномерный по длине двоичный код:
Закодируйте таким образом последовательность символов ВГАГБВ и запишите результат в шестнадцатеричном коде.
Закодируем последовательность букв: ВГАГБВ — 0100110001111010. Теперь разобьём это представление на четвёрки справа налево и переведём полученный набор чисел сначала в десятичный код, затем в шестнадцатеричный:
0100 1100 0111 1010 — 4 12 7 10 — 4С7А.
Для кодирования сообщения, состоящего только из букв А, Б, В и Г, используется неравномерный по длине двоичный код:
Закодируйте таким образом последовательность символов ГАВБВГ и запишите результат в шестнадцатеричном коде.
Закодируем последовательность букв: ГАВБВГ — 0110001011010011. Теперь разобьём это представление на четвёрки справа налево и переведём полученный набор чисел сначала в десятичный код, затем в шестнадцатеричный:
0110 0010 1101 0011 — 6 2 13 3 — 62D3.
Для кодирования сообщения, состоящего только из букв А, Б, В и Г, используется неравномерный по длине двоичный код:
Закодируйте таким образом последовательность символов ГБВАВГ и запишите результат в шестнадцатеричном коде.
Закодируем последовательность букв: ГБВАВГ — 0111101000010011. Теперь разобьём это представление на четвёрки справа налево и переведём полученный набор чисел сначала в десятичный код, затем в шестнадцатеричный:
0111 1010 0001 0011 — 7 10 1 3 — 7A13.
Для 6 букв латинского алфавита заданы их двоичные коды (для некоторых букв из двух бит, для некоторых – из трех). Эти коды представлены в таблице:
001001001111101Какая последовательность из 6 букв закодирована двоичной строкой 011111000101100?
Мы видим, что условия Фано и обратное условие Фано не выполняются, значит, код можно раскодировать неоднозначно.
Будем пробовать различные варианты:
1) 011 11 100 0101100
Первая буква определяется однозначно, её код 011: D.
Вторая буква также определится однозначно — E.
Пусть третья буква B, тогда следующая начинается с кода 010, но таких букв в таблице нет, значит, предположение не верно.
2) 011 11 10 00 101 100
Третья буква — С, потом — A. Мы хотим получить ещё две буквы, чтобы в сумме их было 6, тогда следующая буква — F, и последняя — B.
Окончательно получили ответ: DECAFB.
Примечание. DECACEA не подходит, так как 7 букв.
так же подходит decacea
011 11 10 00 10 11 00
В задании спрашивается о последовательности из шести букв.
Для 5 букв латинского алфавита заданы их двоичные коды (для некоторых букв — из двух бит, для некоторых — из трех). Эти коды представлены в таблице:
Какой набор букв закодирован двоичной строкой 1000110110110? Все буквы в последовательности — разные.
Мы видим, что условия Фано и обратное условие Фано не выполняются, значит, код можно раскодировать неоднозначно.
Будем пробовать разные варианты, отбрасывая те, в которых получаются повторяющиеся буквы:
1) 100 011 01 10 110
Первая буква определяется однозначно, её код 100: a.
Пусть вторая буква — с, тогда следующая буква — d, потом — e и b.
Такой вариант удовлетворет условию, значит, окончательно получили ответ: acdeb.
По каналу связи передаются сообщения, содержащие только восемь букв: А, Б, Г, Е, И, М, Р, Т. Для передачи используется двоичный код, удовлетворяющий условию Фано. Кодовые слова для некоторых букв известны:
| Буква | Кодовое слово |
|---|---|
| А | 11 |
| Б | 0010 |
| Г | 1011 |
| Е | 0011 |
| Буква | Кодовое слово |
|---|---|
| И | |
| М | 01 |
| Р | 000 |
| Т | 1010 |
Укажите кратчайшее кодовое слово для буквы И. Если таких кодов несколько, укажите код с наименьшим числовым значением.
Примечание. Условие Фано означает, что ни одно кодовое слово не является началом другого кодового слова.
Перечислим возможные коды (не использующиеся для кодировки других букв) в порядке возрастания длины и числового значения.
0 — нельзя, Б, Е, М и Р начинаются с 0.
1 — нельзя, буквы А, Г и Т начинаются с 1.
00 — нельзя, Б начинается с 00.
000 — нельзя из-за Р.
001 — нельзя из-за Е.
010 — нельзя из-за М.
011 — нельзя из-за М.
100 — можно использовать.
101 — нельзя из-за Т.
110 — нельзя из-за А.
111 — нельзя из-за А.
Таким образом, наименьшее числовое значение у кодового слова 100 для буквы И.
| Буква | Кодовое слово |
|---|---|
| А | 0101 |
| Б | 1000 |
| Г | |
| Е | 011 |
| Буква | Кодовое слово |
|---|---|
| И | 00 |
| М | 0100 |
| Р | 11 |
| Т | 1001 |
Укажите кратчайшее кодовое слово для буквы Г. Если таких кодов несколько, укажите код с наименьшим числовым значением.
Примечание. Условие Фано означает, что ни одно кодовое слово не является началом другого кодового слова.
Перечислим возможные коды (не использующиеся для кодировки других букв) в порядке возрастания длины и числового значения.
0 — нельзя, А, Е, И и М начинаются с 0.
1 — нельзя, буквы Б, Р и Т начинаются с 1.
10 — нельзя из-за Б и Т.
000 — нельзя из-за И.
001 — нельзя из-за И.
100 — нельзя из-за Т.
101 — можно использовать.
110 — нельзя из-за Р.
111 — нельзя из-за Р.
Таким образом, наименьшее числовое значение у кодового слова 101 для буквы Г.
По каналу связи передаются сообщения, содержащие только восемь букв: А, Б, Г, Е, И, М, Р, Т. Для передачи используется двоичный код, удовлетворяющий условию Фано. Кодовые слова для некоторых букв известны:
| Буква | Кодовое слово |
|---|---|
| А | 11 |
| Б | 0010 |
| Г | 100 |
| Е | 0011 |
| Буква | Кодовое слово |
|---|---|
| И | |
| М | 01 |
| Р | 000 |
| Т |
Укажите кратчайшее кодовое слово для буквы И. Если таких кодов несколько, укажите код с наименьшим числовым значением.
Примечание. Условие Фано означает, что ни одно кодовое слово не является началом другого кодового слова.
Перечислим возможные коды (не использующиеся для кодировки других букв) в порядке возрастания длины и числового значения.
0 — нельзя, Б, Е, М и Р начинаются с 0.
1 — нельзя, А и Г начинаются с 1.
00 — нельзя из-за Б и Р.
000 — нельзя из-за Р.
001 — нельзя из-за Е.
010 — нельзя из-за М.
011 — нельзя из-за М.
100 — нельзя из-за Г.
101 — нельзя, поскольку, если закодировать букву И кодовым словом 101, для буквы Т не будет кодовых слов, удовлетворяющих условию Фано.
110 — нельзя из-за А.
111 — нельзя из-за А.
0000 — нельзя из-за Р.
0001 — нельзя из-за Р.
0010 — нельзя из-за Б.
0011 — нельзя из-за Е.
0100 — нельзя из-за М.
0101 — нельзя из-за М.
0110 — нельзя из-за М.
0111 — нельзя из-за М.
1000 — нельзя из-за Г.
1001 — нельзя из-за Г.
1010 — можно использовать.
1011 — можно использовать.
1100 — нельзя из-за А.
1101 — нельзя из-за А.
1110 — нельзя из-за А.
1111 — нельзя из-за А.
Таким образом, наименьшее числовое значение у кодового слова 1010 для буквы И.
По каналу связи передаются сообщения, содержащие только восемь букв: А, Б, Г, Е, И, М, Р, Т. Для передачи используется двоичный код, удовлетворяющий условию Фано. Кодовые слова для некоторых букв известны:
| Буква | Кодовое слово |
|---|---|
| А | 0101 |
| Б | 101 |
| Г | |
| Е | 011 |
| Буква | Кодовое слово |
|---|---|
| И | 00 |
| М | 0100 |
| Р | 11 |
| Т |
Укажите кратчайшее кодовое слово для буквы Г. Если таких кодов несколько, укажите код с наименьшим числовым значением.
Примечание. Условие Фано означает, что ни одно кодовое слово не является началом другого кодового слова.
Перечислим возможные коды (не использующиеся для кодировки других букв) в порядке возрастания длины и числового значения.
0 — нельзя, А, Е, И и М начинаются с 0.
1 — нельзя, Б и Р начинаются с 1.
01 — нельзя из-за А, Е и М.
000 — нельзя из-за И.
001 — нельзя из-за И.
010 — нельзя из-за М.
011 — нельзя из-за Е.
100 — нельзя, поскольку, если закодировать букву Г кодовым словом 100, для буквы Т не будет кодовых слов, удовлетворяющих условию Фано.
101 — нельзя из-за Б.
110 — нельзя из-за Р.
111 — нельзя из-за Р.
0000 — нельзя из-за И.
0001 — нельзя из-за И.
0010 — нельзя из-за И.
0011 — нельзя из-за И.
0100 — нельзя из-за М.
0101 — нельзя из-за А.
0110 — нельзя из-за Е.
0111 — нельзя из-за Е.
1000 — можно использовать.
1001 — можно использовать.
1010 — нельзя из-за Б.
1011 — нельзя из-за Б.
1100 — нельзя из-за Р.
1101 — нельзя из-за Р.
1110 — нельзя из-за Р.
1111 — нельзя из-за Р.
Таким образом, наименьшее числовое значение у кодового слова 1000 для буквы Г.
По каналу связи передаются шифрованные сообщения, содержащие только десять букв: А, Б, Е, И, К, Л, Р, С, Т, У. Для передачи используется неравномерный двоичный код. Для девяти букв используются кодовые слова. Для буквы А − 00, Е — 010, И — 011, К — 1111, Л — 1101, Р — 1010, С — 1110, Т — 1011, У — 100.
Укажите кратчайшее кодовое слово для буквы Б, при котором код будет удовлетворять условию Фано. Если таких кодов несколько, укажите код с наименьшим числовым значением.
Примечание. Условие Фано означает, что никакое кодовое слово не является началом другого кодового слова. Это обеспечивает возможность однозначной расшифровки закодированных сообщений.
Перечислим возможные коды (не использующиеся для кодировки других букв) в порядке возрастания длины и числового значения.
0 — нельзя, А, Е, И начинаются с 0.
1 — нельзя, буквы К, Л, Р, С, Т, У начинаются с 1.
01 — нельзя из-за Е и И.
10 — нельзя из-за Р, Т и У.
11 — нельзя из-за К, Л, С.
000 — нельзя из-за А.
001 — нельзя из-за А.
101 — нельзя из-за Р и Т.
110 — нельзя из-за Л.
111 — нельзя из-за К.
1000 — нельзя из-за У.
1001 — нельзя из-за У.
1100 — можно использовать.
Таким образом, кратчайшее кодовое слово для буквы Б — 1100.
По каналу связи передаются сообщения, содержащие только десять букв: А, Б, В, Г, Д, Е, И, К, Л, М. Для передачи используется двоичный код, удовлетворяющий условию Фано. Кодовые слова для некоторых букв известны:
| Буква | Кодовое слово |
|---|---|
| А | 00 |
| Б | 010 |
| В | 111 |
| Г | 1100 |
| Д | 1011 |
| Буква | Кодовое слово |
|---|---|
| Е | 011 |
| И | 1010 |
| К | 1001 |
| Л | |
| М | 1000 |
Укажите кратчайшее кодовое слово для буквы Л. Если таких кодов несколько, укажите код с наименьшим числовым значением.
Примечание. Условие Фано означает, что ни одно кодовое слово не является началом другого кодового слова.
Перечислим возможные коды (не использующиеся для кодировки других букв) в порядке возрастания длины и числового значения.
0 — нельзя, А, Б и Е начинаются с 0.
1 — нельзя, В, Г, Д, И, К и М начинаются с 1.
01 — нельзя из-за Б и Е.
10 — нельзя из-за Д, И, К и М.
11 — нельзя из-за В и Г.
000 — нельзя из-за А.
001 — нельзя из-за А.
010 — нельзя из-за Б.
011 — нельзя из-за Е.
100 — нельзя из-за М и К.
101 — нельзя из-за Д и И.
110 — нельзя из-за Г.
111 — нельзя из-за В.
0000 — нельзя из-за А.
0001 — нельзя из-за А.
0010 — нельзя из-за А.
0011 — нельзя из-за А.
0100 — нельзя из-за Б.
0101 — нельзя из-за Б.
0110 — нельзя из-за Е.
0111 — нельзя из-за Е.
1000 — нельзя из-за М.
1001 — нельзя из-за К.
1010 — нельзя из-за И.
1011 — нельзя из-за Д.
1100 — нельзя из-за Г.
1101 — можно использовать.
1110 — нельзя из-за В.
1111 — нельзя из-за В.
Таким образом, кодовым словом для буквы Л, удовлетворяющим условию Фано, является 1101.
По каналу связи передаются сообщения, содержащие только десять букв: А, Б, В, Г, Д, Е, И, К, Л, М. Для передачи используется двоичный код, удовлетворяющий условию Фано. Кодовые слова для некоторых букв известны:
| Буква | Кодовое слово |
|---|---|
| А | 00 |
| Б | 111 |
| В | 010 |
| Г | 1100 |
| Д | 1010 |
| Буква | Кодовое слово |
|---|---|
| Е | 011 |
| И | 1011 |
| К | 1000 |
| Л | |
| М | 1001 |
Укажите кратчайшее кодовое слово для буквы Л. Если таких кодов несколько, укажите код с наименьшим числовым значением.
Примечание. Условие Фано означает, что ни одно кодовое слово не является началом другого кодового слова.
Перечислим возможные коды (не использующиеся для кодировки других букв) в порядке возрастания длины и числового значения.
0 — нельзя, А, В и Е начинаются с 0.
1 — нельзя, Б, Г, Д, И, К и М начинаются с 1.
01 — нельзя из-за В и Е.
10 — нельзя из-за Д, И, К и М.
11 — нельзя из-за Б и Г.
000 — нельзя из-за А.
001 — нельзя из-за А.
010 — нельзя из-за В.
011 — нельзя из-за Е.
100 — нельзя из-за М и К.
101 — нельзя из-за Д и И.
110 — нельзя из-за Г.
111 — нельзя из-за Б.
0000 — нельзя из-за А.
0001 — нельзя из-за А.
0010 — нельзя из-за А.
0011 — нельзя из-за А.
0100 — нельзя из-за В.
0101 — нельзя из-за В.
0110 — нельзя из-за Е.
0111 — нельзя из-за Е.
1000 — нельзя из-за К.
1001 — нельзя из-за М.
1010 — нельзя из-за Д.
1011 — нельзя из-за И.
1100 — нельзя из-за Г.
1101 — можно использовать.
1110 — нельзя из-за Б.
1111 — нельзя из-за Б.
Таким образом, кодовым словом для буквы Л, удовлетворяющим условию Фано, является 1101.
Для 5 букв латинского алфавита заданы их двоичные коды (для некоторых букв — из двух бит, для некоторых — из трех). Эти коды представлены в таблице:
Какой набор букв закодирован двоичной строкой 1100000100110?
Мы видим, что выполняется условие Фано: никакое кодовое слово не является началом другого кодового слова, поэтому однозначно можем раскодировать сообщение с начала.
Разобьём код слева направо по данным таблицы и переведём его в буквы:
110 000 01 001 10 — b a c d e.
Все заглавные буквы русского алфавита закодированы неравномерным двоичным кодом, в котором никакое кодовое слово не является началом другого кодового слова. Это условие обеспечивает возможность однозначной расшифровки закодированных сообщений. Известно, что слову КАША соответствует код 011011010. Какое наименьшее количество двоичных знаков может содержать сообщение, кодирующее слово ОСОКА?
Заметим, что буква А повторяется в слове КАША 2 раза. Буква А стоит на конце слова, кодовое слово 0 для кодирования буквы А использоваться не может, поскольку будет нарушено условие Фано, кодовое слово 010 использоваться не может, поскольку второго такого кодового слова в коде 011011010 не найдётся, значит, буква А кодируется словом 10. Тогда буква Ш соответствует кодовому слову 110, а буква К соответствует кодовому слову 01.
Буква О повторяется в слове ОСОКА 2 раза, закодируем её кодовым словом 00. Букву С кодовым словом длины 3 закодировать нельзя, поскольку не останется кодовых слов для других букв, тогда закодируем её кодовым словом 1110. Тогда количество двоичных знаком в сообщении, кодирующем слово ОСОКА, равно 2 · 4 + 4 = 12.
Все заглавные буквы русского алфавита закодированы неравномерным двоичным кодом, в котором никакое кодовое слово не является началом другого кодового слова. Это условие обеспечивает возможность однозначной расшифровки закодированных сообщений. Известно, что слову УДОД соответствует код 100011101. Какое наименьшее количество двоичных знаков может содержать сообщение, кодирующее слово УДАЧА?
Заметим, что буква Д повторяется в слове УДОД 2 раза. Буква Д стоит на конце слова, кодовое слово 1 для кодирования буквы Д использоваться не может, поскольку будет нарушено условие Фано, кодовое слово 101 использоваться не может, поскольку второго такого кодового слова в коде 100011101 не найдётся, значит, буква Д кодируется словом 01. Тогда буква О соответствует кодовому слову 11, а буква У соответствует кодовому слову 100.
Буква А повторяется в слове УДАЧА 2 раза, закодируем её кодовым словом 00. Букву Ч кодовым словом длины 3 закодировать нельзя, поскольку не останется кодовых слов для других букв, тогда закодируем её кодовым словом 1010. Тогда количество двоичных знаком в сообщении, кодирующем слово УДАЧА, равно 2 · 3 + 3 + 4 = 13.