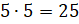Все натуральные числа записанные в порядке образуют что
Конспект урока на тему: «Ряд натуральных чисел»
5 класс Урок №4 _____________
«Ряд натуральных чисел»
Предметный : проверить навыки сложения, вычитания, умножения, деления и сравнения натуральных чисел.
Личностные УУД : формировать учебную мотивацию, адекватную самооценку, необходимость приобретения новых знаний;
Познавательные УУД : формировать навыки нахождения алгоритма решения заданий.
Регулятивные УУД : понимать учебную задачу урока, осуществлять решение учебной задачи под руководством учителя, определять цель учебного задания, контролировать свои действия в процессе его выполнения, обнаруживать и исправлять ошибки, отвечать на итоговые вопросы и достижения;
Коммуникативные УУД : воспитывать любовь к математике, коллективизм, уважение друг к другу, умение слушать, дисциплинированность, самостоятельность мышления.
1.1 Проверка наличия учащихся и готовности к уроку.
1.2 Сообщение темы, целей и последовательности проведения занятия.
У меня для вас вот такое задание проверьте, верно, ли выполнены примеры, если нет то исправьте, поменяв местами две цифры
19+44=63,
132-18=114;
144+206=530(350)
Вы очень хорошо справились с заданием и теперь мы продолжим наш урок.
Разделимся на две команды и справимся с заданием. Нам нужно выполнить это упражнение на скорость.
1. Вступление.
Ребята! Сегодня нам предстоит необычный урок математики. Мы с вами совершим путешествие по огромной и интересной стране, которая называется Математика. В пути вас ждут занимательные задачи, веселые головоломки, забавные, но поучительные факты. Вам встретятся и довольно сложные вопросы. Надеюсь, что вы не забыли захватить с собой любознательность, настойчивость, наблюдательность и смекалку.
2. А вот и первая остановка. Перенесемся в далекое прошлое.
Натуральные числа — одно из старейших математических понятий.
Со временем люди поняли, что шесть камней, шесть коз и шесть палок обладают общим свойством — их количество равно шести.
Натуральные числа — это числа, начиная с 1, получаемые при счете предметов.
1,2,3,4,5.
Наименьшее натуральное число — 1.
Наибольшего натурального числа не существует.
При счёте число ноль не используется. Поэтому ноль не считается натуральным числом.
Записывать числа люди научились гораздо позже, чем считать. Раньше всего они стали изображать единицу одной палочкой, потом двумя палочками — число 2, тремя — число 3.
| — 1, || — 2, ||| — 3, ||||| — 5 и т.д.
Натуральный ряд — это последовательность натуральных чисел, записанных в порядке возрастания:
В натуральном ряду каждое число больше предыдущего на 1.
Натуральный ряд бесконечен, наибольшего натурального числа в нём не существует.
А сейчас мои юные математики ответьте мне на такие вопросы:
— Если надо посчитать количество учеников в классе (учебников на парте, количество карандашей и т.д.), то с какого числа начинаем счет? Итак, какое натуральное число является наименьшим?
— Как отличается каждое следующее число от предыдущего? А от следующего?
— Какое натуральное число предшествует числу 387, стоит за числом 350?
После ответов на вопрос учитель вместе с учениками делает важные выводы:
1. Наименьшим натуральным числом является 1.
2. Наибольшего натурального числа не существует.
3. Все натуральные числа, записанные в порядке возрастания, образуют ряд натуральных чисел.
З акрепление новых знаний и умений учащихся
1. Назовите 10 первых натуральных чисел (ученики с места называют по очереди по одному числу в прямом и обратном направлениях).
Письменное выполнение упражнений (с комментарием учеников с места или у доски)
№№ 1,2,3,4, 6, 8, 10. (Повторить еще раз вывод, сделанный при решении устных упражнений.)
Перед объявлением домашнего задания целесообразно еще раз повторить с учащимися основные понятия, были рассмотрены на уроке.
— Как называют числа, используемые при счете?
— Приведите примеры чисел, не являющихся натуральными.
— Назовите наименьшее натуральное число.
— Существует ли наибольшее натуральное число?
— Какая запись называется рядом натуральных чисел?
Запишите число, которое в натуральном ряду является предыдущем числу:
Математика. 5 класс
Конспект урока
Ряд натуральных чисел. Десятичная система записи натуральных чисел
Перечень вопросов, рассматриваемых в теме:
— десятичная запись натуральных чисел;
— разрядность натуральных чисел
Натуральные числа – числа, которые используют при подсчёте предметов.
Натуральный ряд – последовательность всех натуральных чисел, расположенных в порядке возрастания.
Система счисления – это способ записи чисел с помощью заданного набора специальных знаков (цифр).
Теоретический материал для самостоятельного изучения
С древних времен у человека была потребность в счёте.
Числа, которые используют при подсчёте предметов, называют натуральными числами.
Таким образом, числа: один, два, три, …, десять, …, сто, …, тысяча, …, миллион и так далее – это натуральные числа.
Натуральные числа один, два, три, четыре, пять и так далее, записанные в порядке возрастания и без пропусков, образуют ряд натуральных чисел.
Стоит отметить, что самое маленькое натуральное число – единица (1). В натуральном ряду каждое следующее число на 1 больше предыдущего. Натуральный ряд бесконечен, наибольшего числа в нём нет.
В настоящее время принята десятичная система записи чисел (десятичная система счисления), в которой числа записываются при помощи десяти знаков: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9 – эти знаки называют цифрами.
Одна и та же цифра может иметь различное значение в зависимости от позиции, где она расположена в записи числа. Например, в записи числа пятьсот пятьдесят пять первая справа цифра пять означает пять единиц, вторая – пять десятков, третья – пять сотен.
Вот поэтому десятичную систему счисления называют позиционной.
Натуральные числа, записанные одной цифрой, называют однозначными, а записанные несколькими цифрами – многозначными: двумя – двузначными, тремя – трёхзначными и т. д.
Например, числа 1, 8, 9 – однозначные числа; 10, 66, 89 – двузначные числа; 111, 145 – трёхзначные числа; 123456 – шестизначное число.
Для чтения многозначных чисел их разбивают, начиная справа, на группы по три цифры в каждой (самая левая группа может состоять из одной или двух цифр). Эти группы называются классами.
Первый класс справа называют классом единиц, второй – классом тысяч, третий – классом миллионов, четвёртый – классом миллиардов и т. д.
Натуральные числа
Натуральные числа — это числа, которые используются при счёте или нумерации.
Натуральные числа, записанные в порядке их возрастания (начиная с 1) и без пропусков, образуют ряд натуральных чисел, или короче натуральный ряд:
В натуральном ряду есть первое число — 1 (один или единица), но нет последнего числа — за каждым натуральным числом следует ещё одно, которое больше предшествующего на единицу. Таким образом, есть наименьшее натуральное число — 1, а наибольшего натурального числа не существует. Следовательно 1 — это самое маленькое натуральное число.
Натуральный ряд бесконечен.
Все натуральные числа записать невозможно. Поэтому при записи натурального ряда выписывают подряд несколько первых чисел, следующих друг за другом в натуральном ряду, и в конце ставят многоточие (три точки).
Отсутствие предметов для счёта условились обозначать числом 0 (нуль).
Нуль не считается натуральным числом.
Чётные и нечётные натуральные числа
В натуральном ряду чередуются нечётные и чётные числа, то есть числа, которые делятся на 2 и которые на 2 не делятся. Начинается натуральный ряд с нечётного числа:
Нечётные числа обозначены чёрным цветом, а чётные — красным.
Прямой и обратный счёт
Прямой счёт — это перечисление чисел в порядке их возрастания. Под порядком возрастания, в данном случае, подразумевается что каждое последующее число больше предыдущего на единицу.
Рассмотрим прямой счёт от 1 до 10:
| 1, | 2, | 3, | 4, | 5, | 6, | 7, | 8, | 9, | 10 |
| один | два | три | четыре | пять | шесть | семь | восемь | девять | десять |
Перечисление чисел натурального ряда в порядке их возрастания называется прямым счётом.
Обратный счёт — это перечисление чисел в порядке их убывания. Под порядком убывания, в данном случае, подразумевается что каждое последующее число меньше предыдущего на единицу.
Рассмотрим обратный счёт от 10 до 1:
| 10, | 9, | 8, | 7, | 6, | 5, | 4, | 3, | 2, | 1 |
| десять | девять | восемь | семь | шесть | пять | четыре | три | два | один |
Перечисление чисел натурального ряда в порядке их убывания называется обратным счётом.
Натуральные числа. Ряд натуральных чисел.
История натуральных чисел началась ещё в первобытные времена. Издревле люди считали предметы. Например, в торговле нужен был счет товара или в строительстве счет материала. Да даже в быту тоже приходилось считать вещи, продукты, скот. Сначала числа использовались только для подсчета в жизни, на практике, но в дальнейшем при развитии математики стали частью науки.
Натуральные числа – это числа которые мы используем при счете предметов.
Например: 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18, 19, 20, ….
Нуль не относится к натуральным числам.
Все натуральные числа или назовем множество натуральных чисел обозначается символом N.
Таблица натуральных чисел.
Натуральный ряд.
Натуральные числа, записанные подряд в порядке возрастания, образуют натуральный ряд или ряд натуральных чисел.
Свойства натурального ряда:
Пример №1:
Напишите первых 5 натуральных числа.
Решение:
Натуральные числа начинаются с единицы.
1, 2, 3, 4, 5
Пример №2:
Нуль является натуральным числом?
Ответ: нет.
Пример №3:
Какое первое число в натуральном ряду?
Ответ: натуральный ряд начинается с единицы.
Пример №4:
Какое последнее число в натуральном ряде? Назовите самое большое натуральное число?
Ответ: Натуральный ряд начинается с единицы. Каждое следующее число больше предыдущего на единицу, поэтому последнего числа не существует. Самого большого числа нет.
Пример №5:
У единицы в натуральном ряду есть предыдущее число?
Ответ: нет, потому что единица является первым числом в натуральном ряду.
Пример №6:
Назовите следующее число в натуральном ряду за числами: а)5, б)67, в)9998.
Ответ: а)6, б)68, в)9999.
Пример №7:
Сколько чисел находится в натуральном ряду между числами: а)1 и 5, б)14 и 19.
Решение:
а) 1, 2, 3, 4, 5 – три числа находятся между числами 1 и 5.
б) 14, 15, 16, 17, 18, 19 – четыре числа находятся между числами 14 и 19.
Пример №8:
Назовите предыдущее число за числом 11.
Ответ: 10.
Пример №9:
Какие числа применяются при счете предметов?
Ответ: натуральные числа.
Ряд натуральных чисел
Урок 1. Математика 5 класс ФГОС
В данный момент вы не можете посмотреть или раздать видеоурок ученикам
Чтобы получить доступ к этому и другим видеоурокам комплекта, вам нужно добавить его в личный кабинет, приобрев в каталоге.
Получите невероятные возможности
Конспект урока «Ряд натуральных чисел»
Представим себе такую историю…
Раз, два, три, четыре, пять,
Научились мы считать.
Ну а дальше мы не знаем,
Может, вместе посчитаем?
Шесть – конфеты любим есть,
Семь – мы помогаем всем,
Восемь – мы друзей в беде не бросим,
Девять – учимся на пять,
Вспоминал считалочку Саша.
– Саша, а что ты делаешь? Для чего это ты считаешь? – спросил Паша.
– Я хочу привести в порядок свою коллекцию солдатиков! Как из них всех выбрать кого-то на первое место? Они же такие все одинаковые! – воскликнул Саша.
– Я совсем не вижу проблемы! Посмотри: на каждом из твоих солдатиков стоит цифра. Ну так и поставь их по порядку! – возразил Паша.
– Как это? Что значит по порядку? – удивился Саша.
– Саша, ты такой смешной! Ты что, в школе не изучал натуральные числа? – с недоумением спросил Паша.
– Какие числа? На-ту-раль-ные. – ещё больше запутался Саша.
– Да, да, Саша! Именно натуральные! – продолжил Паша. Давай я тебя познакомлю со своим другом Электрошей. И он сейчас тебе всё объяснит.
– Мы каждый день отвечаем на вопрос «Сколько?» – начал Электроша. При этом, помимо слов «много» или «мало», мы называем конкретные числа. Кстати, а вы знаете, что число является основным понятием математики, которое сложилось в ходе очень длительного исторического развития? А чтобы ответить на вопрос «Сколько?», надо сосчитать.
– Вот, Саша, сколько тебе лет? – спросил Электроша.
– Одиннадцать! – уверенно ответил Саша.
– Все те числа, которые вы слышите с самого рождения, и, кстати, они же будут сопровождать вас постоянно и повсюду, помогают нам считать различные предметы и отвечают на вопрос «Сколько?» – продолжал Электроша. –Такие числа называются натуральными.
Запомните! Числа 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12 и так далее, используемые при счёте предметов, называют натуральными.
Вот, например, числа 1, 5, 7, 11, 31, 365, 2017, 1 000 000 – это натуральные числа. Но важно понимать, что не все числа, которыми вы пользуетесь, – натуральные. Так, например, числа 0, 

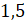
Вообще, название «натуральное» происходит от латинского слова natura – ‘природа’. То есть натуральные числа как бы происходят от природы, но, конечно, изобретены они человеческим мозгом.
Впервые термин «натуральное число» появился в трудах римского философа Боэция, жившего ещё в V – VI веках.
– Спасибо, Электроша! – с радостью воскликнул Саша. – Теперь я всё понял и могу с лёгкостью привести в порядок свою коллекцию солдатиков. И тут Саша быстренько начал расставлять солдатиков по своему порядку.
– Саша, ты не всё понял! – остановил Сашу Паша. – Ведь числа тоже имеют свой порядок.
– Порядок? – удивился Саша.
– Да, Саша! Числа тоже хотят жить в порядке! – сказал Электроша.
Если выстроить все числа по порядку, только не просто, как ты сейчас расставил своих солдатиков, а от меньшего числа к большему, то получится натуральный ряд.
Запомните! Все натуральные числа, записанные в порядке возрастания, образуют ряд натуральных чисел (или натуральный ряд).
А вот что тебе ещё нужно знать о натуральном ряде:
1) натуральный ряд чисел начинается с числа 1. То есть первым числом натурального ряда является число 1, вторым – число 2, третьим – число 3 и так далее;
2) в натуральном ряду за каждым числом следует ещё одно число, большее предыдущего на единицу. То есть для того, чтобы получить следующее натуральное число, надо прибавить к текущему натуральному числу единицу;
3) число один не имеет предыдущего. Значит, мы можем с уверенностью говорить, что среди натуральных чисел есть наименьшее число – и это число 1, но нет наибольшего;
4) в натуральном ряду чисел нет последнего числа. Другими словами, натуральный ряд чисел бесконечен, так как к любому числу всегда можно прибавить ещё единицу;
5) натуральных чисел бесконечно много, а вот несуществующих предметов человеку не приходило в голову считать. Поэтому число ноль не натуральное число, так как оно не может получиться в результате счёта;
6) выписать весь натуральный ряд невозможно. Обычно поступают так: выписывают подряд несколько первых чисел натурального ряда, а затем ставят многоточие.
– Вот теперь, Электроша, я точно всё понял – обрадовался Саша. – Посмотри, как я расставил своих солдатиков!
– Да, Саша, на этот раз ты сделал всё правильно! – подбодрил Электроша Сашу. – И раз ты всё понял, предлагаю вам с Пашей закрепить знания на выполнении некоторых заданий.
Задание первое: из указанных чисел выберите натуральные.
11, 
Решение: числа 11, 251, 12 800 – натуральные, так как мы их используем при счёте, а вот те числа, которые остались, не будут натуральными.
Следующее задание: из записанных рядов чисел назовите натуральный.
Решение: в этом задании из всех записанных числовых рядов натуральным будет только второй ряд. Первый ряд не подходит, потому что вначале стоит цифра 0, а мы знаем, что 0 не является натуральным числом. Третий ряд не подходит, так как числа записаны в нём не в порядке возрастания, а в порядке убывания. А вот последний ряд не подходит, потому что в нём каждое последующее число больше предыдущего не на единицу, а на два.
– Саша, Паша, вы отлично справляетесь с заданиями! – с радостью сказал Электроша. – А значит, вы обязательно справитесь с моей непростой задачей.
Задача. 11 коров за 3 дня съедают 33 мешка сена. Сколько мешков сена надо 5 коровам на 5 дней?
Решение: сначала нам нужно найти, сколько мешков сена съедают 11 коров за один день. Для этого 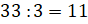
Затем мы можем узнать, сколько мешков сена съедает 1 корова за 1 день. Для этого 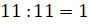
Теперь узнаем, сколько мешков сена съедят 5 коров за 1 день. Для этого 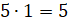
И осталось выяснить, сколько мешков сена съедят 5 коров за 5 дней. Для этого