Все что удалось найти
В Антарктиду за метеоритом: что удалось найти участникам научной экспедиции?
Уральские ученые, искавшие метеорит в Антарктиде, застряли в ЮАР. Чем закончилась эта экспедиция и когда ее участники вернутся домой, телеканалу «МИР 24» рассказал руководитель поискового отряда метеоритной экспедиции Уральского федерального университета Александр Пастухович.
— Как сообщают СМИ, сейчас вы находитесь в ЮАР. Что произошло?
— Новый штамм коронавируса в этом не виноват?
Александр Пастухович: Косвенно новый штамм здесь причем, потому что «Турецкие авиалинии» отменили свои рейсы именно по причине обнаружения нового штамма, но, на наш взгляд (мы третий день в Кейптауне), вся ситуация слегка преувеличена, и никакой особой драмы нет. Здесь первый уровень локдауна – все работает, на улице достаточно много людей, соблюдающих обычные меры предосторожности, как и у нас: маска, санитайзеры – ничего неприятного здесь не происходит.
— Нашли ли вы то, что хотели, в результате экспедиции?
Александр Пастухович: Не совсем так. Нам хотелось найти зоны накопления метеоритного вещества, они есть в тех районах, где мы были. К сожалению, погода внесла коррективы в нашу экспедицию, мы просто не успели всю программу выполнить. Тем не менее, одна находка точно есть, ее совершил горный гид, участник нашей экспедиции во время одного разведывательного выхода.
Погода – причина закрытия полевого периода, то есть мы раньше снялись со льда, чем планировали, потому что возникли трудности. Мы предвидели, но перед ураганом устоять не могли. Нашу палатку порвало, и в условиях, когда метеопрогноз не предвещал ничего хорошего, мы решили завершить экспедиционный этап, вызвали самолет, нас сняли со льда, а дальше началась непогода, и в аэропорту, вблизи станции «Новолазоревская», мы ожидали вылета на континент, в Кейптаун.
— Сколько времени потребовалось на подготовку экспедиции?
Александр Пастухович: Практически год мы готовили этот выезд, очень много вопросов было по снаряжению, по питанию, но самый основной вопрос был финансовый, потому что проект недешевый. Связано это с тем, что логистическое звено экспедиции – переброска грузов в Кейптаун, оттуда на станцию «Новолазоревская», переброска участников – все это – самолеты, топливо, которое в Антарктиде стоит недешево. Нас обеспечивала компания «Алси Ай» этими услугами. Она же обеспечивала и безопасность, то есть тот вызов самолета, который пришлось делать в срочном режиме, был подтвержден.
Состав экспедиции – шесть человек. Профессор Казанского университета Данис Нургалиев, два горных гида – Руслан Колунин и Виталий Лазо, космонавт Сергей Кудь-Сверчков, командированный в состав экспедиции Роскосмосом, бизнесмен и основной инвестор Андрей Назаров и я – руководитель поискового отряда, научный сотрудник Уральского федерального университета Александр Пастухович.
— У вас на родине метеориты сами падают с неба. Почему пришлось ехать на поиски в Антарктиду?
Александр Пастухович: Как раз тот метеорит, который упал у нас на родине, спровоцировал нас на международные поездки. Метеоритная экспедиция Уральского федерального университета работает с 1986 года. Раньше предметами ее интереса были метеориты, упавшие на территории России и стран бывшего Союза.
На протяжении многих тысячелетий, миллионов лет космическое вещество попадало в лед Антарктиды. Ледник постоянно движется и переносит все, что накопил в своей толще, от центра матерка к периферии. Часть ледника упирается в горные массивы, но, поскольку давление льда огромное, лед продолжает двигаться вверх. Это уникальная ситуация, когда в горах ледник не скатывается вниз, не образуясь вблизи вершин гор, а у подножия гор наползает к вершинам. За счет сильнейших ветров, которые бывают в Антарктиде зимой, и скорости около 300 километров в час, воздействия солнца лед разрушается. Все, что было в его толще, практически вываливается на поверхность. Образуются морены вблизи гор. На этих участках голубого льда накапливается метеоритное вещество.
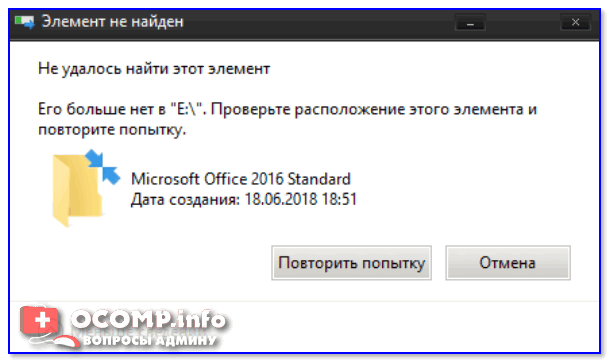
«Не удалось найти этот элемент. Его больше нет в «E:\». Проверьте расположение элемента и повторите попытку» — ошибка при попытке удалить папку

Вообще, чаще всего это происходит из-за:
Собственно, не так давно и сам сталкивался с этой ошибкой. Чуть ниже приведу несколько шагов для устранения оной. Инструкция должна помочь в не зависимости от причины. 😉
Не удалось найти этот элемент. Его больше нет в «E:\». Проверьте расположение элемента и повторите попытку (пример ошибки)
Что можно посоветовать для устранения ошибки
👉 ШАГ 1
Банально, но самая первая рекомендация — просто перезагрузить компьютер (ноутбук).
Нередко, когда ошибка связана с некорректной работой проводника и файловой системы («не удаляемый» элемент (файл/папка) — после перезагрузки начнет «вести» себя, как и все остальные, и вы без труда удалите ее. ).
Перезагрузка компьютера / Windows 10
👉 ШАГ 2
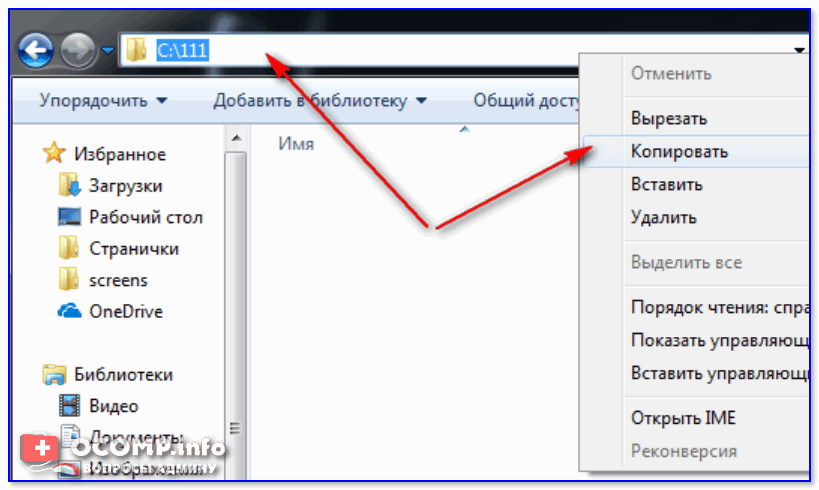
Далее скопировать путь до той папки, которая не удаляется классическим способом (в моем случае «C:\111»).
Копируем путь до папки, которую удаляем
После, в командной строке потребуется написать следующее: RD /S «C:\111» (и нажать Enter).
Это команда удалит и сам указанный каталог, и все файлы, что в нем есть. Будьте аккуратны, т.к. командная строка не всегда переспрашивает.
Пример удаления каталога
Более подробно о том, как избавиться от папки/файла с помощью командной строки
👉 ШАГ 3
Еще один весьма действенный способ решения вопроса — воспользоваться безопасным режимом загрузки Windows (при нем будут запущены только самые необходимые приложения и службы). И уже из-под него попробовать удалить нужные файл/папку.
Подробно не останавливаюсь — ссылка ниже поможет загрузить ОС в нужном режиме (работа же в нем не отличается от обычного режима).
Как зайти в безопасный режим в Windows 7÷10 — см. инструкцию.
👉 ШАГ 4
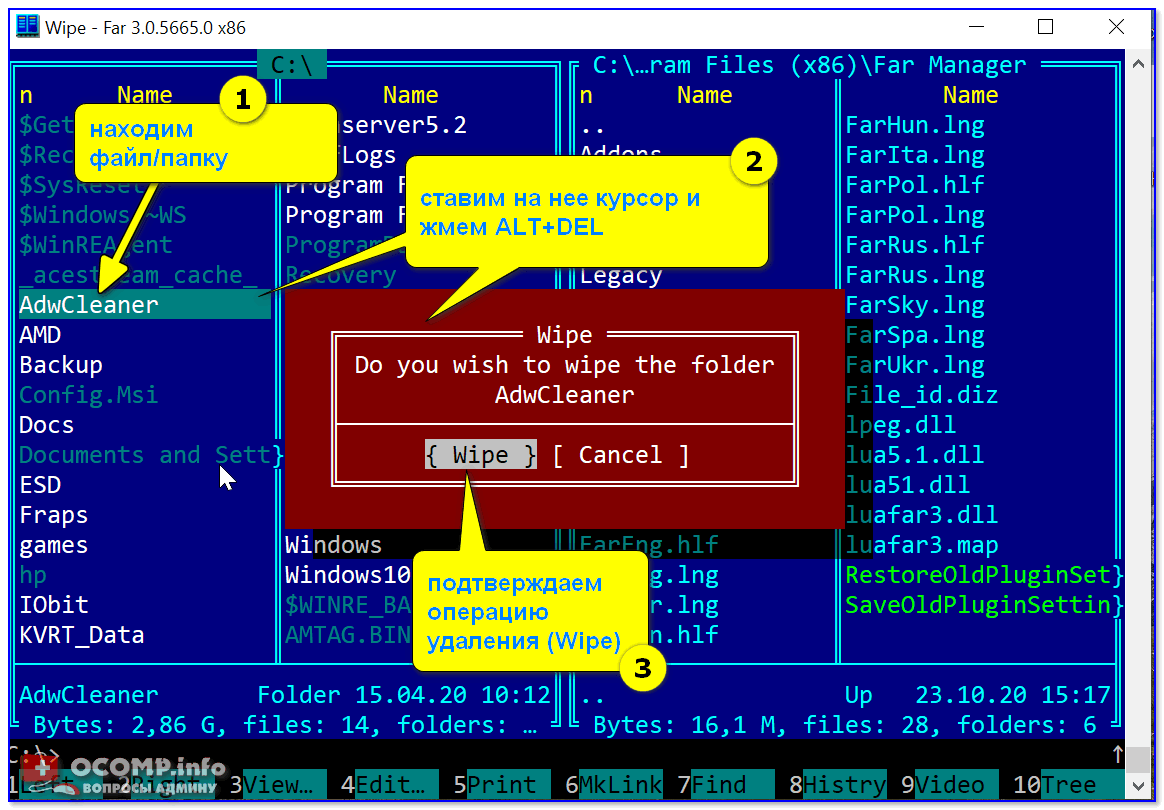
Есть один замечательный коммандер (👉 речь о FAR) для работы с большим количеством файлов. Сейчас для многих он смотрится как анахронизм, но поверьте — эта штука до сих пор делает некоторые вещи надежнее, чем проводник!
Так вот, если в нем выделить «проблемный» элемент (скажем, папку) и нажать сочетание ALT+DEL — то запустится функция Wipe (уничтожение файла). Она отлично справляется со своей задачей (даже с весьма проблемными файлами), рекомендую попробовать!
Примечание : будьте аккуратнее с этим способом, т.к. файлы будут удалены, минуя корзину.
Far Manager — пример удаления папки
👉 ШАГ 5
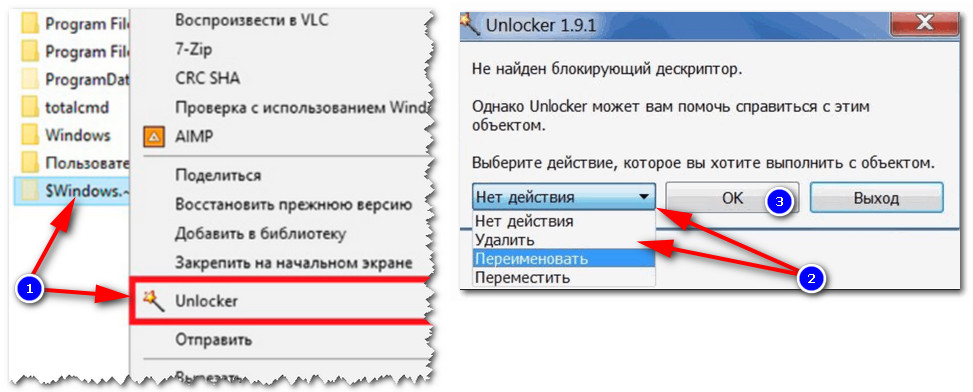
Программы для удаления не удаляемых файлов и папок — моя подборка
Как удалить папку в Unlocker
👉 ШАГ 6
Разумеется, после, вы сможете «прошерстить» все свои накопители на компьютере и удалить с них любые файлы. Только будьте аккуратнее, т.к. при работе с LiveCD вы сможете удалять и системные, и обычные, и скрытые файлы.
LiveCD для аварийного восстановления Windows — моя подборка (там же в заметке указано как подготовить такой накопитель)
Какие программы есть на диске «Стрельца. » // Пример рабочего стола при загрузке с LiveCD-флешки
Если из вышеперечисленного ничего не помогло — проверьте свой диск на ошибки (в ряде случаев при возникновении «потерянных элементов» могут быть найдены ошибки файловой системы. При проверке, кстати, они исправляются автоматически).
Если удалось вопрос решить иначе — дайте знать ⇓ (заранее спасибо!).
LiveInternetLiveInternet
—Музыка
—Подписка по e-mail
Промежуточные выводы. Всё что удалось найти в процессе поиска.Часть 2
Руны Русского Рода и топология.
Я. СТЮАРТ
Тополог — это тот, кто набивает чучела? Из разговоров
Одним из самых неожиданных явлений в развитии математики XX в. стал головокружительный взлет науки, известной под названием топология. Желая пояснить, что такое топология, иногда говорят, что это «геометрия на резиновой поверхности».Это малопонятное и туманное описание позволяет тем не менее уловить суть предмета. Топология изучает те свойства геометрических объектов, которые сохраняются при непрерывных преобразованиях.Непрерывные преобразования характеризуются тем, что точки, расположенные «близко одна к другой» до преобразования, остаются такими и после того, как преобразование закончено. При топологических преобразованиях разрешается растягивать и изгибать, но не разрешается рвать и ломать. (Однако, с одной оговоркой: когда речь идет о преобразованиях, нас не интересует, что происходит в процессе этих преобразований, важны только начальное положение и конечный результат. Поэтому допускаются, скажем, разрезы по каким-то линиям, которые потом склеиваются по тем же линиям. Например, если шнурок завязан узлом и его концы соединены, можно разрезать его где-то, развязать узел и снова соединить на месте разреза. В этом смысле выражение «геометрия на резиновой поверхности» не слишком удачно.) Можно было бы дать строгое определение «непрерывности», однако пока мы ограничимся интуитивным представлением о ней.
Какого рода свойства являются топологическими? Ясно, что не те, которые изучаются в обычной евклидовой геометрии. Прямолинейность не есть топологическое свойство, потому что прямую линию можно изогнуть, и она станет волнистой. Треугольность — тоже не является топологическим свойством, ибо треугольник можно непрерывно деформировать в окружность (рисунок 1).
Итак, в топологии треугольник и окружность — одно и то же.Длины отрезков, величины углов, площади — все эти понятия изменяются при непрерывных преобразованиях, и о них следует забыть. Очень немногие привычные понятия геометрии годятся для топологии, поэтому приходится искать новые. Этим топология трудна для начинающего, пока он не постигнет сути дела.
Образцом топологического свойства объекта служит наличие дырки у бублика (причем довольно тонкая сторона этого дела — тот факт, что дырка не является частью бублика). Какую бы непрерывную деформацию ни претерпел бублик, дырка останется. Другое топологическое свойство — наличие края. Поверхность сферы не имеет края, а пустая полусфера имеет, и никакое непрерывное преобразование не в состоянии это изменить .
Из книги: Стюарт Я. Концепции современной математики (Минск: Вышэйшая школа. 1980).
С уществует очень много различных непрерывных преобразований, поэтому топологам что бублик, что какая-нибудь другая штука с одной дыркой — все едино( в этом мы убедимся в следующем разделе). У тополога меньше объектов изучения, и в этом смысле предмет изучения в топологии проще, чем в большинстве других разделов математики (хотя сама топология как предмет отнюдь не проще других). В этом одна из причин того, что топология превратилась в мощный инструмент математики в целом: ее простота и общность обеспечили ей широкий круг применений.
Топологическая эквивалентность
Два топологических пространства топологически эквивалентны, если можно непрерывным образом перейти от одного из них к другому и непрерывным же образом вернуться обратно. Часто говорят, что тополог не отличает бублика от кофейной чашки.
Это как раз и есть пример топологической эквивалентности (рисунок 3).Нам приходится вводить требование непрерывности как прямого отображения, так и обратного к нему, по следующей причине. Возьмем два куска глины и слепим их вместе. Такое преобразование непрерывно, поскольку близкие друг к другу точки останутся таковыми (рисунок 4). Однако при обратном преобразовании один кусок распадается на два (рисунок 5), и, следовательно, близкие точки по разные стороны от линии раздела окажутся далеко друг от друга, т. е. обратное преобразование не будет непрерывным. Такие преобразования нам не подходят.
В качестве упражнения попытайтесь разбить топологические пространства, изображенные на рисунке 6, на классы топологически эквивалентных.
Некоторые необычные пространства
Вы, наверное, слышали о ленте (или листе) Мебиуса, которую можно получить из бумажной полоски, склеив ее края после поворота на 180° (рисунок 7).
Лента Мёбиуса топологически не то же самое, что цилиндрическая лента, склеенная из той же полоски. Она имеет только один край (посчитай!). Поскольку количество краев — топологическое свойство, а цилиндрическая лента имеет два края, эти две ленты топологически неэквивалентны.
Известно еще одно свойство ленты Мёбиуса — то, что она имеет лишь одну сторону. Цилиндрическую ленту можно раскрасить двумя цветами — одну сторону красным, другую синим. Проделать то же самое с лентой Мёбиуса не удастся.
К сожалению, свойство односторонности трудно описать математически строго и в то же время достаточно наглядно. Ведь наша лента не имеет толщины, и каждая ее точка находится «на» обеих сторонах, подобно тому как каждая точка плоскости лежит на обеих ее сторонах. В топологии мы должны рассматривать эту ленту как некое пространство, а не подмножество евклидова пространства, и тогда не совсем очевидно, является ли количество сторон топологическим свойством.
Чтобы пояснить эту мысль, позвольте мне задать вопрос: сколько сторон у трехмерного евклидова пространства?
Думаю, большинство ответит: «ни одной». Ведь наше пространство продолжается до бесконечности в любом направлении, какие же у него могут быть стороны?
Иначе говоря, количество сторон зависит от того, рассматривать ли плоскость саму по себе или как часть трехмерного пространства. То же самое относится и к трехмерному пространству: если в качестве четвертого измерения ввести время, то окажется, что наше пространство имеет две стороны — прошлое и будущее.
0 листе Мёбиуса «Квант, писал неоднократно (см. например. № 1 за 1990 год. а также «Калейдоскоп» № 11 за 1991 год).
Надеюсь, теперь понятно, насколько трудно даже объяснить, что понимается под числом сторон, не говоря уж о том, чтобы понять, топологическое это свойство или нет.
Однако существует все-таки одно явление, которое могут наблюдать воображаемые жители ленты Мёбиуса, не выходя за пределы своего «пространства», и которое позволяет дать математическое описание «односторонности». Предположим, что эти создания имеют две руки, причем их большие пальцы направлены в разные стороны. Тогда им доступны понятия «правый» и «левый». Кроме того, допустим, что они носят варежки (рисунок 8).
Однажды просыпается такое существо и видит, что все его правые варежки куда-то подевались и остались одни левые. Проявив находчивость, оно берет одну варежку и переносит ее вдоль ленты, как показано на рисунке 9.
К большому нашему (но не его!) удивлению, левая варежка превратилась в правую. Правда, при этом и левая рука воображаемого существа превратилась в правую, а правая — в левую, но зато оно получило годную пару варежек.
Можете сами убедиться в этом, склеив ленту Мёбиуса из бумаги (и тогда, чтобы увидеть, что делается «на другой стороне» бумаги, придется смотреть на свет сквозь нее), а лучше из прозрачной пленки. Вместо этого можете воспользоваться своими двумя руками и воображаемой лентой Мёбиуса. Поскольку руки не двумерны, следите только за их очертаниями. Держите руки перед собой ладонями наружу, пальцы вверх, большие пальцы прижаты друг к другу. Левую руку оставьте на месте, а правую двигайте вдоль воображаемой ленты Мёбиуса следующим образом. Поднимите правый локоть, чтобы ладонь наклонилась, затем поворачивайте ее вниз от себя, поднимайте локоть еще выше, пока рука не окажется в положении тыльной стороной к вам, пальцами вниз. Теперь сдвиньте ее влево на уровень левой руки и отведите от себя большой палец, чтобы ладонь стала к вам ребром. В идеале следовало бы поворачивать и дальше правую руку, но анатомия не позволяет, поэтому поверните левую руку большим пальцем к себе и соедините ладони ребром к ребру, левая вниз, правая вверх.
Вот это неудобное положение и получается после того, как ваша правая рука опишет ленту Мёбиуса (а левая немного продвинется ей навстречу). Чтобы стало полегче, держите руки в том же положении одну относительно другой, но передвиньте правую немного вправо, а левую за ней следом. Теперь нужно перевернуть правую руку снизу вверх на поверхности ленты Мёбиуса. Для этого опустите правый локоть, продолжая держать руку ладонью наружу. Теперь обе кисти направлены вверх, левая ладонью внутрь, правая — наружу. Сложите их вместе. Вы убедились в том, как точно они совпали. Если говорить только об очертаниях, то ваша правая рука, описав ленту Мёбиуса, стала левой (а заодно вы получили превосходный пример стиля рассуждений, известного у математиков под названием «размахивание руками»).
Если соединить края двух лент Мёбиуса, получится поверхность, называемая бутылкой Клейна (рисунок 10). У нее нет краев, и она неориентируема, потому что неориентируемы ленты Мёбиуса. Кроме того, ее нельзя вложить в трехмерное пространство так, чтобы не было самопересечений.
Бутылку Клейна можно описать по-другому: представьте себе квадрат, стороны которого склеены так, как показывают стрелки на рисунке 11. (Сначала верхняя сторона склеивается с нижней и получается цилиндр. Затем, чтобы правильно склеить края цилиндра, его надо согнуть и протолкнуть сквозь самого себя.) При помощи этой же диаграммы можно убедиться в том, что бутылка Клейна действительно получается из двух лент Мёбиуса: разрежем ее, как показано на рисунке 12.
Иногда можно услышать какие-то утверждения о внутренней и наружной стороне бутылки Клейна. Они бессмысленны: в трехмерном пространстве ее построить нельзя, а в четырехмерном, где ее можно сделать без самопересечений, говорить о внутренности бутылки «Клейна — все равно, что говорить о внутренности окружности в трехмерном пространстве,— можно в нее войти и из нее выйти без всяких препятствий.
Склеиванием сторон квадрата можно получить еще два интересных пространства: тор и проективную плоскость (называемую так из-за ее связи с проективной геометрией) (рис. 13).
Проективная плоскость представляет собой ленту Мёбиуса, приклеенную край в край к кругу. Чтобы построить ее в трехмерном пространстве, надо превратить край ленты Мёбиуса в окружность. Лента при этом будет перекручиваться и самопересекаться, образуя так называемый скрещенный колпак (рисунок 14). Закрыв его отверстие, получим проективную плоскость (рисунок 15).
Наконец, познакомимся еще с одним занятным пространством — рогатой сферой Александера (рисунок 16)). Оно строится так.
0 ней вы можете прочитать в «Кванте»№ 6 за1990 год.
Вытянем из сферы два рога, расщепим надвое их концы и переплетем их между собой, расщепим надвое новые концы и снова переплетем их, и так далее до бесконечности. Хотите — верьте, хотите — нет, но то, что получается, топологически эквивалентно сфере: способ вытягивания рогов можно задать при помощи подходящей функции, которая определяет топологическую эквивалентность. Однако наружное пространство рогатой сферы уже не будет топологически эквивалентно пространству вне обычной сферы.
В самом деле, с обычной сферы соскакивает любая надетая на нее петля (рисунок 17), а на рогатой сфере она может запутаться в рогах (рисунок 18). И здесь снова заботы причиняет не сама поверхность, а окружающее ее пространство.
Теорема о волосатом шаре
Мы немного поговорили о понятиях, которые вводятся в топологии, и объектах, которые в ней изучаются.
Теперь приведем пример топологической теоремы. Если внимательно посмотреть, как растет шерсть у собаки, можно обнаружить, что вдоль спины она разделяется «на пробор», а другой «пробор» идет вдоль живота. С точки зрения топологии собака — это шар (если считать, что пасть у нее закрыта, и пренебречь внутренними органами); чтобы в этом убедиться, достаточно «втянуть» ей ноги и немного ее «раздуть» (рисунок 19).
Можно задаться таким вопросом: удастся ли так «причесать» собаку, чтобы не стало «проборов». В результате получился бы волосатый шар, не имеющий ни «проборов», ни «макушек», изображенных на рисунке 20.
Этот вопрос относится к топологии, ибо при любой непрерывной деформации такого шара гладкая шерсть останется гладкой, а «пробор» останется «пробором». Топологические методы позволяют установить (хотя это нелегко), что гладко причесать шар невозможно. (В правильной формулировке задачи говорится о «векторных полях» на сфере, но этому вполне соответствует интуитивное представление о волосатом шаре.)
Лучшее, чего можно добиться,— причесать волосы так, что останется лишь одна «макушка» — точка, в которой нарушается гладкость (рис. 21).
Не будем углубляться здесь в доказательство этой теоремы, однако заметим, что ее значение выходит за рамки причудливых применений к воображаемым гладким собакам.
Поверхность Земли представляет собой сферу. Если для какого-то момента времени изобразить на сфере направления воздушных потоков в атмосфере Земли, т. е. направления всех ветров, дующих над поверхностью Земли, то получится своего рода «прическа» на этой сфере, где роль волос будут играть линии, изображающие потоки. Наша теорема утверждает, что не существует гладкой системы ветров (за исключением случая полного безветрия, что, однако, невозможно, но по другим причинам), т. е. где-то всегда есть циклон.
Таким образом, зная только форму Земли, мы уже можем делать заключения о поведении ветров без всяких сведений о том, куда они дуют на самом деле.
А вот на тороидальной планете возможен постоянный ветер без циклонов, поскольку волосатый тор можно причесать требуемым образом (рисунок 22).
Дальнейшее изучение, основанное уже на более подробных сведениях о ветрах, показывает, что гладкий поток скорее будет обвиваться вокруг тора, как на рисунке 23.
Известны и многие другие приложения теоремы о волосатом шаре. Например, в алгебре она применяется для доказательства теоремы о том, что каждое уравнение, левая часть которого — многочлен, имеет корни в поле комплексных чисел (так называемая «основная теорема алгебры»).
Теперь посмотрим конкретно на применение топологии в Рунах Русского Рода.
Топология Рун Русского Рода, находка РБ (Раб Божий)!
» Пт Дек 05, 2008 10:24 pm
Я пожалуй начну с этого. Для меня очень важна топология любой конструкции. Т.е. если есть исходное, каким образом можно это представить иначе без нарушения основ исходного.
Исходная полусота