Волчья квинта что это
Волчья квинта
Волчья квинта (букв. пер. с нем. Wolfsquinte) — музыкальный интервал, название очень фальшивой квинты, которая возникала в различных музыкальных строях.
Пифагорейская волчья квинта
При использовании пифагорейского строя, ступени 12-ступенного звукоряда определялись с помощью наложенных друг на друга чистых квинт. После двенадцати шагов (каждый из которых определял одну из ступеней) основной тон должен был бы повториться через семь октав. На самом деле двенадцать квинт превосходят семь октав на пифагорейскую комму. В результате один из шагов приходилось делать меньше (у́же) на пифагорейскую комму, и последняя квинта имела ощутимый дефект.
Волчья квинта имеет следующие соотношения частот:

Пифагорейская волчья квинта меньше чистой квинты (соотношение частот 3 : 2 ≈ 701,96 цента) на ≈ 23,46 цента (пифагорейскую комму), и меньше равномерно темперированной квинты (700 центов) на ≈ 21,50 цента.
Среднетоновая волчья квинта
В среднетоновом строе также есть одна квинта, которую старались не использовать (чаще всего Gis-Dis), по аналогии с пифагорейским строем её тоже иногда называют волчьей квинтой. В отличие от пифагорейской эта больше натуральной и ближе к малой сексте, чем к тритону, поэтому диссонанс несколько мягче.

Среднетоновая волчья квинта превосходит чистую квинту на ≈ 35,68 цента, больше равномерно темперированной квинты на ≈ 37,64 цента и больше среднетоновой квинты на ≈ 41,06 цента.
Равномерно темперированный строй
Волчья квинта считалась сильным диссонансом, и её старались избегать при сочинении и исполнении музыки. С развитием музыкальной мысли постепенно возникла потребность в широком применении транспозиций и модуляций. На струнных смычковых инструментах есть возможность скорректировать интервал во время игры. Однако с массовым распространением инструментов с фиксированным строем (и прежде всего клавишных) проблема стала острой, пока не разрешилась распространением равномерно темперированного строя, в котором пифагорейская комма равномерно распределялась по всем ступеням и теряла остроту.
 Музыкальные интервалы Музыкальные интервалы | ||
|---|---|---|
| Простые | Прима • Секунда • Терция • Кварта • Квинта • Секста • Септима • Октава | 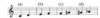 |
| Составные | Нона • Децима • Ундецима • Дуодецима • Терцдецима • Квартдецима • Квинтдецима | |
| Особые | Схизма • Диасхизма • Комма • Диеса • Лимма • Апотома • Дитон • Полудитон • Тритон • Волчья квинта • Цент • Полутон • Миллиоктава | |
Полезное
Смотреть что такое «Волчья квинта» в других словарях:
Квинта — (лат. quinta пятая) музыкальный интервал шириной в пять ступеней, обозначается цифрой 5. Содержание 1 Разновидности квинты 1.1 Чистая квинта … Википедия
Интервал (музыка) — У этого термина существуют и другие значения, см. Интервал. Интервал (от лат. intervallum промежуток, расстояние; разница, несходство) в музыке соотношение между двумя звуками определённой высоты. Наименьшей единицей измерения… … Википедия
Интервалы — Интервал (от лат. intervallum промежуток, расстояние, разница) высотное соотношение двух звуков (ступеней), имеющих определённые названия. Нижний звук интервала называется его основанием, верхний вершиной. Содержание 1 Классификация интервалов … Википедия
Музыкальный интервал — Интервал (от лат. intervallum промежуток, расстояние, разница) высотное соотношение двух звуков (ступеней), имеющих определённые названия. Нижний звук интервала называется его основанием, верхний вершиной. Содержание 1 Классификация интервалов … Википедия
Пифагорейский строй — Пифагорейский строй, Пифагоров строй сформулированный в соответствии с математическими расчётами интервальных величин, свойственными пифагорейской школе гармоники, способ построения отношений между звуками определённой высоты. Со времён поздней… … Википедия
Комма — Комма (греч. κόμμα отрезок) в теории музыки общее название для микроинтервалов величиной около 1/7 1/10 целого тона, возникающих, как правило, при сопоставлении однотипных интервалов в различных музыкальных строях[1]. Наиболее известны … Википедия
Диасхизма — (др. греч. διασχίσμα, лат. diaschisma), также уменьшённая комма[1] микроинтервал, равный разности дидимовой (синтонической) коммы и схизмы и, таким образом, имеющий отношение частот верхнего и нижнего звука … Википедия
Тритон (интервал) — У этого термина существуют и другие значения, см. Тритон. Увеличенная кварта … Википедия
Натуральный строй — Равномерная темперизация. Натуральный строй музыкальный строй, использующий интервалы, построенные на основе обертонов. Октава (1:2), квинта (2:3) … Википедия
Дуодецима — (лат. duodecimus двенадцатый; подразумевается 12 я по порядку ступень звукоряда, считая от первой, примы) музыкальный интервал шириной в 12 ступеней, обозначается цифрой 12. Чаще всего рассматривается как составной интервал, то есть… … Википедия
Самый сильный диссонанс
Что такое диссонанс? Простыми словами – это неблагозвучное, неприятное сочетание различных звуков. Почему же такие сочетания присутствуют среди интервалов и аккордов? Откуда они взялись и зачем они нужны?
Путешествие Одиссея
Как мы выяснили в предыдущей заметке, во времена Античности господствовал пифагорейский строй. В нем все звуки строя получаются простым делением струны на 2 или на 3 равные части. Деление на две части просто смещает звук на октаву. А вот деление на три рождает новые ноты.
Возникает законный вопрос: а когда нам прекратить это деление? Из каждой новой ноты, поделив струну на 3, мы можем получить ещё одну. Таким образом мы можем получить в музыкальной системе 1000 или 100000 звуков. Где же нам стоит остановиться?
Когда Одиссей, герой древнегреческой поэмы, возвращался на свою Итаку, его на пути ждало множество препятствий. И каждое из них задерживало его в путешествии до тех пор, пока он не находил, как с ним справиться.
На пути развития музыкальных систем тоже возникали свои препятствия. Они на какое-то время затормаживали процесс появления новых нот, затем их преодолевали и плыли дальше, где встречали следующую преграду. Этими преградами были диссонансы.
Попробуем понять, что такое диссонанс.
Точное определение этого явления мы сможем получить, когда поймем физическое устройство звука. Но сейчас точность нам не требуется, нам достаточно объяснить это простыми словами.
Итак, у нас есть струна. Мы можем поделить ее на 2 или на 3 части. Получим таким образом октаву и дуодециму. Октава звучит более консонантно, и это понятно – деление на 2 проще, чем деление на 3. В свою очередь дуодецима будет звучать консонантней, чем струна поделенная на 5 частей (такое деление даст терцию через две октавы), потому что деление на 3 проще, чем деление на 5.
Теперь вспомним, как строилась, например, квинта. Мы делили струну на 3 части, а затем увеличивали получившуюся длину в 2 раза (рис.1).
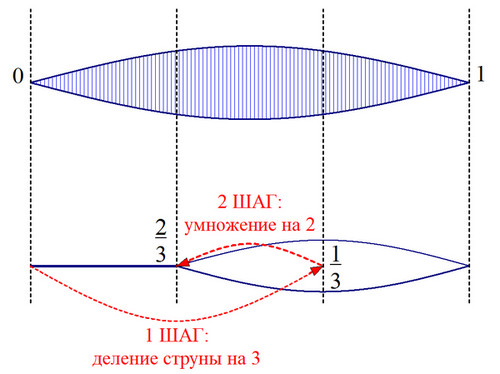
Как видим, чтобы построить квинту, нам нужно сделать не один, а два шага, а, следовательно, квинта будет звучать менее консонантно, чем октава или дуодецима. С каждым шагом мы как бы всё дальше и дальше уходим от исходной ноты.
Можно сформулировать простое правило для определения консонантности:
чем меньше шагов мы делаем, и чем проще сами эти шаги, тем консонантней будет интервал.
Вернемся к построениям.
Итак, люди выбрали первый звук (будем для удобства считать, что это до, хотя сами древние греки так его не называли) и начали строить другие ноты, деля или умножая длину струны на 3.
Сначала получили два звука, которые к до оказались самыми близкими – это фа и соль (рис.2). Соль получается, если длину струны уменьшить в 3 раза, а фа – наоборот, если в 3 раза увеличить.

Индекс π по-прежнему будет означать, что речь идет о нотах пифагорейского строя.
Если перенести эти ноты в ту же октаву, где расположена нота до, то интервалы до них будут называться кварта (до-фа) и квинта (до-соль). Это два весьма примечательных интервала. При переходе от пифагорейского строя к натуральному, когда изменились почти все интервалы, построение кварты и квинты осталось неизменным. Формирование тональности шло с самым непосредственным участием этих нот, именно на них строились доминанта и субдоминанта. Эти интервалы оказались настолько консонантными, что господствовали в музыке вплоть до эпохи романтизма, да и после им отводилась весьма значительная роль.
Но мы отвлеклись от диссонансов. На этих трех нотах построения не остановились. Сруну продолжили делить на 3 части и дуодецима за дуодецимой получать новые и новые звуки.
Первое препятствие возникло на пятом шаге, когда к до (исходная нота), ре, фа, соль, ля добавилась нота ми (рис.3).

Между нотами ми и фа образовался интервал, который показался людям того времени жутко диссонантным. Этим интервалом была малая секунда.
Малая секунда ми-фа — гармоническая
Встретив этот интервал, решили, что включать ми в систему уже не стоит, надо остановиться на 5 нотах. Так первая система оказалась 5-нотной, ее назвали пентатоника. Все интервалы в ней весьма консонантны. Пентатонику до сих пор можно встретить в народной музыке. Иногда как особая краска она присутствует и в классике.
Со временем к звучанию малой секунды привыкли и поняли, что если использовать ее умеренно и к месту, то с ней вполне можно жить. И следующим препятствием стал шаг номер 7 (рис.4).

Новая нота оказалась настолько диссонантной, что ей даже решили не давать собственного названия, а назвали фа-диез (обозначается f#). Собственно диез и означает тот интервал, который образовался между этими двумя нотами: фа и фа-диез. Звучит он так:
Интервал фа и фа-диез — гармонический
Если не выходить «за пределы диеза», то у нас получается 7-нотный строй – диатоника. Большинство классических и современных музыкальных систем являются 7-ступенными, то есть наследуют в этом отношении пифагорейской диатонике.
Несмотря на такое огромное значение диатоники, Одиссей поплыл дальше. Преодолев преграду в виде диеза, он увидел открытый простор, в котором можно набрать в систему целых 12 нот. Но вот 13-ая образовывала страшный диссонанс – пифагорову комму.
Пожалуй, можно сказать, что комма явила собой Сциллу и Харибду в одном лице. На преодоление этого препятствия ушли не годы и даже не столетия. Только спустя пару тысяч лет, в XX веке нашей эры, музыканты всерьез обратились к микрохроматическим системам, которые содержат больше 12 нот. Разумеется, на протяжении этих веков предпринимались отдельные попытки добавить в октаву ещё несколько звуков, но попытки эти были настолько робкими, что говорить о их значительном вкладе в музыкальную культуру, к сожалению, не приходится.
Можно ли считать попытки XX века в полной мере удачными? Вошли ли микрохроматические системы в музыкальный обиход? Вернемся к этому вопросу, но перед этим рассмотрим ещё несколько диссонансов уже не из пифагорейского строя.
Волк и дьявол
Когда мы приводили диссонантные интервалы из пифагорейского строя, мы немного лукавили. То есть и малая секунда и диез были, но слышали их тогда немного иначе.
Дело в том, что музыка античности по преимуществу была монодического склада. Проще говоря, одновременно звучала только одна нота, а вертикаль – одновременное сочетание нескольких звуков – почти не использовалась. Поэтому и малую секунду и диез античные любители музыки, как правило, слышали так:
Малая секунда ми-фа — мелодическая
Полутон фа и фа-диез — мелодический
А вот с развитием вертикали в полной мере зазвучали гармонические (вертикальные) интервалы, в том числе и диссонантные.
Первым в этом ряду стоит назвать тритон.
Тритоном он называется, не потому что он похож на земноводное, а потому что в нем от нижнего звука до верхнего ровно три целых тона (то есть шесть полутонов, шесть клавиш фортепиано). Интересно, что и на латыни он называется tritonus.
Этот интервал можно построить и в пифагорейском строе и в натуральном. И там и там он будет звучать диссонантно.
Чтобы построить его в пифагорейском строе придется поделить струну на 3 части 6 раз, а затем получившуюся длину 10 раз увеличить вдвое. Получится, что длина струны будет выражаться дробью 729/1024. Стоит ли говорить, что при таком количестве шагов о консонансе говорить не приходится.
В натуральном строе ситуация немногим лучше. Натуральный тритон можно получить так: два раза поделить длину струны на 3 (т.е. делим на 9), затем поделить еще на 5 (итого делим на 45 частей), а потом 5 раз увеличить вдвое. В результате длина струны будет 32/45, что хоть и немного проще, но консонанса не сулит.
По слухам в средневековье этот интервал назывался «дьяволом в музыке».
Но важнее для развития музыки оказалось другое созвучие – волчья квинта.
Откуда же такой интервал берется? Зачем он нужен?
Предположим мы набираем звуки в натуральный строй от ноты до. В нем нота ре получается, если мы два раза поделим сруну на 3 части (сделаем два дуодецимальных шага вперед). А нота ля образуется несколько иначе: для ее получения нам нужно увеличить струну в 3 раза (сделать по дуодецимам один шаг назад), а затем поделить получившуюся длину струны на 5 частей (то есть взять натуральную терцию, которой как раз и не было в пифагорейском строе). В результате между длинами струн нот ре и ля мы получим не простое соотношение 2/3 (чистую квинту), а соотношение 40/27 (волчью квинту). Как видим из соотношения, это созвучие и не может быть консонантным.
А почему бы нам не взять ноту ля, которая бы составляла чистую квинту от ре? Дело в том, что тогда у нас появятся две ноты ля – «квинтовая от ре» и «натуральная». Но с «квинтовой» ля возникнут те же проблемы, что были с ре – ей понадобится своя квинта, и у нас появятся уже две ноты ми.
И этот процесс неостановим. На месте одной головы гидры появляется две. Решив одну проблему, мы порождаем новую.
Решение проблемы волчьих квинт оказалось радикальным. Создали равномерно темперированный строй, где и «квинтовая» ля и «натуральная» заменились одной нотой – темперированной ля, которая давала чуть-чуть фальшивые интервалы со всеми другими нотами, но при этом фальшь была едва заметной, а не столь очевидной, как в волчьей квинте.
Так волчья квинта, как опытный морской волк, привела музыкальный корабль к весьма неожиданным берегам – равномерно темперированному строю.
Краткая история диссонансов
Чему же нас учит краткая история диссонансов? Какой опыт можно извлечь из путешествия длиною в несколько веков?
Мало кто сейчас будет считать малую секунду таким уж диссонантным интервалом, особенно в мелодическом расположении. А ведь всего каких-нибудь две с половиной тысячи лет назад это было так. И тритон вошел в музыкальную практику, многие музыкальные произведения, даже в популярной музыке, строятся с самым серьезным участием тритона.
Например, с тритонов начинается композиция Джими Хендрикса Purple Haze:
Постепенно всё больше и больше диссонансов переходят в разряд «не таких уж и диссонансов» или «почти консонансов». Дело не в том, что наш слух испортился, и мы не слышим, что звучание таких интервалов и аккордов резкое или отталкивающее. Дело в том, что наш музыкальный опыт растет, и сложные многошаговые построения мы уже можем воспринимать как необычные, неординарные и по-своему интересные.
Есть музыканты, которым и волчьи квинты или коммы, представленные в данной статье, не покажутся ужасающими, они отнесутся к ним как к своеобразному, сложному материалу, с которым можно поработать в создании столь же сложной и своеобразной музыки.
 rainy_sunny
rainy_sunny
Rainy Sunny Journal
pieces of my mind
Нижеследующие таблицы наглядно показывают ситуацию с чистотой интервалов в разных исторических строях.
Размеры интервалов указаны в центах и округлены до целых центов.
Чистые интервалы выделены полужирным. Интервалы, которые отличаются от чистых на 10-20 центов выделены тёмно-красным, а отклонения более чем на 20 центов — ярко красным. Получается так:
чёрный жирный — совершенно чистый интервал;
просто чёрный — очень чистый (отклонение менее 10 центов);
тёмно-красный — не очень чистый (отклонение от 10 до 20 центов);
ярко-красный — совсем фальшивый (отклонение больше 20 центов).
«Волчья» квинта (и всё, что из неё вытекает) в пифагоровом и среднетоновом строе у меня получилась в разных местах, так вышло. Вообще, её положение зависит от двух вещей — от какой ноты начали строить звукоряд и где решили замыкать квинтовый круг. Суть от этого не меняется. В любом случае, в пифагоровом строю будет одна «волчья» квинта из 12-ти (вопрос лишь в том, какая именно), две «волчьи» большие секунды из 12-ти, и так далее.
Расстояния от До до остальных нот в той же октаве:
| Пифагоров | Среднетоновый на 1/4 коммы | Натуральный | Хорошо темперированный (3-я темперация Веркмейстера) | Равномерно темперированный | |
| С | 0 | 0 | 0 | 0 | 0 |
| С#/Db | 114 | 117 | 112 | 90 | 100 |
| D | 204 | 193 | 204 | 192 | 200 |
| D#/Eb | 294 | 310 | 316 | 294 | 300 |
| E | 408 | 386 | 386 | 390 | 400 |
| F | 498 | 503 | 498 | 498 | 500 |
| F#/Gb | 612 | 580 | 590 | 588 | 600 |
| G | 702 | 697 | 702 | 696 | 700 |
| G#/Ab | 815 | 814 | 814 | 792 | 800 |
| A | 906 | 890 | 884 | 888 | 900 |
| A#/Bb | 996 | 1007 | 996 | 996 | 1000 |
| B | 1110 | 1083 | 1088 | 1092 | 1100 |
| С | 1200 | 1200 | 1200 | 1200 | 1200 |
Размер полутонов:
| Пифагоров | Среднетоновый на 1/4 коммы | Натуральный | Хорошо темперированный (3-я темперация Веркмейстера) | Равномерно темперированный | |
| С-C# | 90 | 117 | 112 | 90 | 100 |
| С#-D | 114 | 76 | 92 | 102 | 100 |
| D-D# | 90 | 117 | 112 | 102 | 100 |
| D#-E | 114 | 76 | 70 | 96 | 100 |
| E-F | 90 | 117 | 112 | 108 | 100 |
| F-F# | 90 | 77 | 92 | 90 | 100 |
| F#-G | 114 | 117 | 112 | 108 | 100 |
| G-G# | 90 | 117 | 112 | 96 | 100 |
| G#-A | 114 | 76 | 70 | 96 | 100 |
| A-A# | 90 | 117 | 112 | 108 | 100 |
| A#-B | 114 | 76 | 92 | 96 | 100 |
| B-C | 90 | 117 | 112 | 108 | 100 |
Сложно сказать, что именно является натуральным полутоном: их несколько и все натуральные.
Один полутон равен 16 /15 или 112 центов. Это — разница между чистой квартой и чистой большой терцией. Другой — 25 /24 или 70 центов, это разница между чистой большой и чистой малой терциями. Ещё один — 135 /128, или 92 цента.
Поэтому в этой таблице я не стал выделять никаких отклонений.
Размер тонов:
| Пифагоров | Среднетоновый на 1/4 коммы | Натуральный | Хорошо темперированный (3-я темперация Веркмейстера) | Равномерно темперированный | |
| C-D | 204 | 193 | 204 | 192 | 200 |
| С#-D# | 204 | 193 | 204 | 204 | 200 |
| D-E | 204 | 193 | 182 | 198 | 200 |
| D#-F | 204 | 193 | 182 | 204 | 200 |
| E-F# | 180 | 194 | 204 | 198 | 200 |
| F-G | 204 | 194 | 204 | 198 | 200 |
| F#-G# | 204 | 234 | 224 | 204 | 200 |
| G-A | 204 | 193 | 182 | 192 | 200 |
| G#-A# | 204 | 193 | 182 | 204 | 200 |
| A-B | 204 | 193 | 204 | 204 | 200 |
| A#-C | 204 | 193 | 204 | 204 | 200 |
| B-C# | 180 | 234 | 224 | 198 | 200 |
Малые терции:
| Пифагоров | Среднетоновый на 1/4 коммы | Натуральный | Хорошо темперированный (3-я темперация Веркмейстера) | Равномерно темперированный | |
| C-D# | 294 | 310 | 316 | 294 | 300 |
| С#-E | 318 | 279 | 274 | 300 | 300 |
| D-F | 294 | 310 | 294 | 306 | 300 |
| D#-F# | 294 | 270 | 274 | 294 | 300 |
| E-G | 294 | 311 | 316 | 306 | 300 |
| F-G# | 294 | 311 | 316 | 294 | 300 |
| F#-A | 318 | 310 | 294 | 300 | 300 |
| G-A# | 294 | 310 | 294 | 300 | 300 |
| G#-B | 318 | 269 | 274 | 300 | 300 |
| A-C | 294 | 310 | 316 | 312 | 300 |
| A#-C# | 294 | 310 | 316 | 294 | 300 |
| B-D | 294 | 310 | 316 | 300 | 300 |
Большие терции:
| Пифагоров | Среднетоновый на 1/4 коммы | Натуральный | Хорошо темперированный (3-я темперация Веркмейстера) | Равномерно темперированный | |
| C-E | 408 | 386 | 386 | 390 | 400 |
| С#-F | 408 | 386 | 386 | 408 | 400 |
| D-F# | 384 | 387 | 386 | 396 | 400 |
| D#-G | 408 | 387 | 386 | 402 | 400 |
| E-G# | 384 | 428 | 428 | 402 | 400 |
| F-A | 408 | 387 | 386 | 390 | 400 |
| F#-A# | 408 | 427 | 406 | 408 | 400 |
| G-B | 408 | 386 | 386 | 396 | 400 |
| G#-C | 408 | 386 | 386 | 408 | 400 |
| A-C# | 384 | 427 | 428 | 402 | 400 |
| A#-D | 408 | 386 | 408 | 396 | 400 |
| B-D# | 384 | 427 | 428 | 402 | 400 |
Квинты:
| Пифагоров | Среднетоновый на 1/4 коммы | Натуральный | Хорошо темперированный (3-я темперация Веркмейстера) | Равномерно темперированный | |
| C-G | 702 | 697 | 702 | 696 | 700 |
| С#-G# | 702 | 697 | 702 | 702 | 700 |
| D-A | 702 | 697 | 680 | 696 | 700 |
| D#-A# | 702 | 697 | 680 | 702 | 700 |
| E-B | 702 | 697 | 702 | 702 | 700 |
| F-C | 702 | 697 | 702 | 702 | 700 |
| F#-C# | 702 | 737 | 722 | 702 | 700 |
| G-D | 702 | 696 | 702 | 696 | 700 |
| G#-D# | 702 | 696 | 702 | 702 | 700 |
| A-E | 702 | 696 | 702 | 702 | 700 |
| A#-F | 702 | 696 | 702 | 702 | 700 |
| B-F# | 678 | 697 | 702 | 696 | 700 |
Квинте (и её «сестре» кварте) везёт больше, чем другим интервалам: почти во всех строях она очень близка к чистой (за исключением «волчьих квинт»).
Строи и особенности гармонии взаимно влияли друг на друга. В пифагоровом строе не было чистых терций, поэтому терции в то время не были основой гармонии, а были диссонансным, проходным интервалом. Музыка была более суровая и менее полифоничная. Придумали строи, в которых чистые терции — развился язык классической гармонии, основанной на аккордах, созданных из терций (все эти мажоры и миноры). Появилось желание более свободно менять тональности и усложнить гармонию — мысль двинулась в направлении хорошо темперированных строёв и равномерной темперации.
Так ли плохи нечистые терции? Послушайте чистые и равномерно темперированныe аккорды (РТ).
Да, РТ-аккорды звучат не так чисто, они немножко «плавают». Но можно сказать и наоборот: чистые аккорды по сравнению с РТ-аккордами кажутся застывшими и безжизненными. Мы уже вполне привыкли к тому, что аккорды немного «дышат» — почему бы и нет. А если хочется чистоты — так никто не мешает поиграть на синтезаторах или плагинах, которые поддерживают just intonation, со всеми её плюсами и минусами.
Пара слов для гитаристов. Гитара — инструмент изначально рассчитанный на равномерную темперацию. Расстояние между ладами каждый раз убывает в 2 1 /12 раз. Поэтому все интервалы, которые мы берём на гитаре — равномерно темперированные.
А вот флажолеты дают исключительно чистые интервалы, они иначе не могут, потому что основаны на гармониках струны (их принцип действия я описывал в прошлый раз).
Напомню:
Флажолет на 12-м ладу увеличивает частоту в 2 раза и увеличивает высоту ноты на октаву ( 2 /1)
Флажолет на 7-м или 19-м ладу увеличивает частоту в 3 раза и прибавляет к ноте октаву и ЧИСТУЮ квинту (3=2* 3 /2)
Флажолет на 5-м или 24-м ладу увеличивает частоту в 4 раза и прибавляет к ноте две октавы (2*2=4).
Флажолет на 4-м, 9-м или 16-м ладу увеличивает частоту в 5 раз и прибавляет к ноте две октавы плюс ЧИСТУЮ большую терцию (5=2*2* 5 /4).
Поэтому даже если идеально отстроить гитару по мензуре и настроить по тюнеру, то часть флажолетов будут давать «неправильные» ноты.
А именно — флажолеты на 12-м или 5-м ладу будут чистыми (потому что октавы)
Флажолеты на 7-м или 19-м ладу будут на 2 цента высить, потому что именно настолько чистая квинта больше равномерно темперированной.
А вот флажолеты на 4-м, 9-м или 16-м ладу будут сильно — на 14 центов — низить, потому что именно настолько чистая большая терция меньше равномерно темперированной.
Это стоит учитывать при настройке гитары по флажолетам. На идеально настроенной гитаре нота на 8 ладу струны B и флажолет на 12 ладу струны G — это одна и та же нота. Флажолеты на 7 ладу струны G и на 5 ладу струны D — уже отличаются на 2 цента, потому что флажолет на 7 ладу на 2 цента высит.
А вот флажолет на 5 ладу струны B и флажолет на 4 ладу струны G — это уже очень разные ноты. В первом случае это «правильная» B, которая на равномерно темперированную большую терцию выше, чем G, а во втором случае — нота, которая на чистую большую терцию выше, чем G. Разница между ними — 14 центов. Так что если подстроить струну G так, чтобы эти два флажолета совпали, гитара будет совершенно расстроена.
Ещё одна иллюстрация различия между чистой и РТ-большой терцией. Флажолет на 4 ладу нижней струны E и нота на 4 ладу верхней струны E — это вроде бы одна и та же нота G#, но на самом деле нет. В первом случае это нота на чистую терцию выше верхней Ми, во втором — на равномерно темперированную терцию.
Отсюда вывод: настраивать гитару по флажолетам можно, но ни в коем случае не используйте при этом флажолеты на 4-м ладу (и все остальные, дающие чистую терцию: 9 и 16).
Немного видео, которые мне попались в процессе написания поста:
Альбом 2007 года в чистом строе:
Канон Пахельбеля в трёх строях: натуральном, среднетоновом и равномерно темперированном:
Произведение 2008 года в среднетоновом строе:
 rainy_sunny
rainy_sunny