Вода для корабля то же что для бизнеса
Вода для корабля то же что для бизнеса
Перечислите все возможные способы измерить высоту здания с помощью барометра.
Вы претендуете на должность руководителя рекламной компании. Утром в день собеседования вы решили поместить некую рекламу в такое место, где президент мог бы увидеть ее по дороге на работу. Что это будет за реклама? Каково должно быть внешнее оформление рекламы, чтобы президент наверняка обратил на нее внимание?
Развитие метафорического мышления
Заполните пробелы в сравнениях и метафорах.
Интересный способ ввести себя в состояние творчества заключается в том, чтобы вообразить смешение различных видов восприятия, то есть представить себе способность ощущать вкус звуков, слышать цвета, обонять ощущения. Попробуйте проделать что-то в таком роде.
Чем пахнет слово “участвовать”?
Каково на ощупь число семь?
Какой вкус у голубого цвета?
Как выглядит идея свободы?
Какая форма у среды?
Каков вкус радости?
Создадите командную игру с двумя мячами?
Переконструируете человеческое тело?
Переконструируете человеческое лицо?
Создадите проект дома, не имеющего прямых стен?
Каждый день принимайте в постели такую позу, какой вы еще никогда не принимали.
Каждый день изобретайте новое слово и придумывайте для него значение.
Каждый день выдумывайте новую мысль.
Каждый день делайте умственную гимнастику.
В течение месяца каждый день придумывайте новый способ чистить зубы.
Две минуты на творчество
Очень часто наше творческое кровообращение осуществляется намного интенсивнее, когда мы попадаем в безвыходное положение и нам ничего не остается, как только проявить изобретательность.
Выполните следующие упражнения.
За две минуты придайте своей правой руке максимальное количество новых положений. А теперь за две минуты произнесите слова “сегодня вечером” с наибольшим количеством различных интонаций.
На рисунке три фрагмента. За две минуты составьте как можно больше узоров с использованием только этих трех фрагментов.
Не останавливайтесь на первом же правильном решении. Возьмите себе за правило заглядывать чуть-чуть дальше и копать чуть-чуть глубже.
Деловое общение
Изложение принципов делового общения базируется на объединении научной и практической проблематики таких дисциплин, как лингвистика, риторика, психология, этика, логика, менеджмент.
Учит преодолевать барьеры в общении, искусно вести деловой разговор, переговоры, совещания, убеждать, не позволять собеседнику манипулировать собой, успешно выступать перед аудиторией.
Адресовано студентам экономических специальностей, а также всем, чья профессиональная деятельность осуществляется в сфере коммуникации: менеджерам, маркетологам, специалистам в области рекламного дела и PR, бизнесменам. Может быть использовано как для аудиторных занятий, так и для самостоятельной работы.
Денис Александрович Шевчук
Тема 1. Вербальные средства коммуникации
Тема 2. Слушание в деловой коммуникации
Тема 3. Невербальная коммуникация
Занятие 1. Невербальные средства коммуникации
Занятие 2. Организация пространственной среды
Тема 4. Сознательное/бессознательное и ложь в речевой коммуникации
Тема 5. Манипуляции в общении
Тема 6. Гендерный аспект коммуникативного поведения
Тема 7. Критика и комплименты в деловой коммуникации
Занятие 1. Комплименты в деловой коммуникации
Занятие 2. Критика в деловой коммуникации
Тема 8. Вопросы и ответы в деловой коммуникации
Тема 9. Барьеры в общении
Тема 10. Имидж делового человека
Занятие 1. Формирование вербального имиджа
Занятие 2. Самопрезентация
Тема 11. Публичная Речь
Тема 12. Психолого-коммуникативный потенциал деловых партнеров
Тема 13. Русский Речевой Этикет
Тема 14. Формы деловой коммуникации
Занятие 1. Правила убеждения
Занятие 2. Деловая беседа по телефону
Занятие 3. Дискуссия
Занятие 4. Деловые переговоры
Занятие 5. Деловые совещания
Занятие 7. Презентация
Денис Александрович Шевчук
Тема 1. Вербальные средства коммуникации
Менеджер – наемный управленец, начальник!
Если у вас нет ни одного подчиненного – вы не менеджер, а максимум специалист!
Заберите у меня все, чем я обладаю. Но оставьте мне мою речь. И скоро я обрету все, что имел.
Общение является основной составляющей труда таких специалистов, как менеджеры, юристы, психологи, бизнесмены, рекламисты и т. п. Поэтому владение общением, средствами вербальной и невербальной коммуникации необходимо для каждого делового человека.
К вербальным средствам общения относится человеческая речь. Специалистами по общению подсчитано, что современный деловой человек за день произносит примерно 30 тыс. слов, или более 3 тысяч слов в час. Его величество Общение правит людьми, их жизнью, их развитием, их поведением, их познанием мира и самих себя как части этого мира. И всякая попытка осмыслить коммуникацию между людьми, понять, что ей мешает и что способствует, важна и оправдана, так как общение – это столп, стержень, основа существования человека.
В зависимости от намерений коммуникантов (что-то сообщить, узнать, выразить оценку, отношение, побудить к чему-либо, договориться и т. д.) возникают разнообразные речевые тексты. В любом тексте (письменном или устном) реализуется система языка.
Итак, язык – это система знаков и способов их соединения, которая служит орудием выражения мыслей, чувств и волеизъявлений людей и является важнейшим средством человеческого общения.
А еще язык – это зеркало культуры, в нем отражается не только реальный мир, окружающий человека, не только реальные условия его жизни, но и общественное самосознание народа, его менталитет, национальный характер, образ жизни, традиции, обычаи, мораль, система ценностей.
Язык – это и передатчик, носитель культуры, он передает сокровища национальной культуры, хранящейся в нем, из поколения в поколение. Овладевая родным языком, дети усваивают вместе с ним и обобщенный культурный опыт предшествующих поколений.
Язык – это и орудие, инструмент культуры. Он формирует личность человека, носителя языка, через навязанные ему языком и заложенные в языке видение мира, менталитет, отношение к людям…
Таким образом, язык используется в самых разных функциях. Сколько их? Лучше других ответил на этот вопрос американский лингвист Э. Сепир: «Трудно с точностью установить функции языка, так как он настолько глубоко коренится во всем человеческом поведении, что остается очень немногое в функциональной стороне нашей сознательной деятельности, где язык не принимал бы участия». Назовем основные:
Коммуникативная. Язык выступает в роли основного средства общения. Благодаря наличию у языка такой функции люди имеют возможность полноценного общения с себе подобными.
Познавательная. Язык как выражение деятельности сознания. Основную часть информации о мире мы получаем через язык.
Аккумулятивная. Язык как средство накопления и хранения знаний. Приобретенные опыт и знания человек старается удержать, чтобы использовать их в будущем. В повседневной жизни нас выручают конспекты, дневники, записные книжки. А «записными книжками» всего человечества являются разного рода памятники письменности и многовековая художественная литература, которая была бы невозможна без существования письменного языка.
Конструктивная. Язык как средство формирования мыслей. При помощи языка мысль «материализуется», приобретает звуковую форму. Выраженная словесно, мысль становится отчетливой, ясной для самого говорящего.
Эмоциональная. Язык как одно из средств выражения чувств и эмоций. Эта функция реализуется в речи только тогда, когда прямо выражается эмоциональное отношение человека к тому, о чем он говорит. Большую роль при этом играет интонация.
Контактоустанавливающая. Язык как средство установления контакта между людьми. Иногда общение как бы бесцельно, информативность его нулевая, лишь готовится почва для дальнейшего плодотворного, доверительного общения.
Этническая. Язык как средство объединения народа.
Типы приема и передачи информации
Человек использует естественный язык с двумя целями: не только передать информацию, но еще и понять мир. Но оказывается, что прием и передача информации могут быть осуществлены, кроме естественного языка, как минимум еще двумя способами, соответствующими двум интеллектуальным возможностям человека: образному мышлению и сенсорике.
Образное мышление – это восприятие мира в виде картинки. Художественное полотно или скульптура – это тоже текст, несущий немалую смысловую нагрузку. Мышление зрительными образами знакомо каждому человеку, например, когда он вспоминает эпизод из своей жизни, не расчлененный словесно, а зафиксированный сознанием в виде фотографии.
Под сенсорикой понимается биоэнергетический способ обмена информацией, при котором человек ничего не говорит и ничего не демонстрирует, но при этом передает информацию, и она воспринимается теми, к кому она направлена.
Таким образом, при глубоком анализе становится очевидным, что от природы люди наделены 3 разными формами мышления: естественным языком, образным и сенсорным мышлением.
Как работает естественный язык в своей речевой функции, мы наблюдаем постоянно: текст → слова → слово → значение.
Как функционирует образное мышление? Восприятие мира осуществляется не расчлененно, а единой картинкой. Живописное полотно нельзя расчленить на элементы (как текст), оно воспринимается целиком. Человек получает больше информации, переходя от правой к левой части картины. Значит, по сравнению с естественным языком это принципиально иная форма восприятия. Люди с развитым образным мышлением воспринимают мир иначе, чем люди с преобладанием мыслительной языковой функции.
10 Парадоксов, которые очень удивят вас
Парадокс — это утверждение, которое, по-видимому, противоречит само себе и, тем не менее, может быть правдой. Большинство логических парадоксов, как известно, являются неверными аргументами, но, несмотря на это, они важны для продвижения критического мышления. Ниже представлены десять парадоксов, которые совершенно точно удивят вас.
1. Парадокс ценности: Почему вода дешевле, чем бриллианты, ведь для выживания людям нужна вода, а не бриллианты?
Парадокс ценности (также известный как парадокс воды и алмазов, или парадокс Смита) является явным противоречием, состоящим в следующем: несмотря на то, что вода куда более полезна для выживания человека, бриллианты обладают намного более высокой ценой на рынке. На низших уровнях потребления, вода обладает гораздо более высокой предельной полезностью, чем бриллианты, и таким образом, является более ценной. Люди используют воду в больших количествах, чем они используют бриллианты, таким образом, предельная полезность и цена воды ниже, чем у бриллиантов.
При объяснении парадокса алмазов, ученые, изучающие предельную полезность, разъясняют, что в расчёт берётся не общая польза бриллиантов или воды, а польза каждой единицы воды и бриллиантов по отдельности. Абсолютно верно, что совокупная полезность воды имеет огромное значение для людей, так как они нуждаются в ней, чтобы выжить. Однако исходя из того, что воды в мире очень много, предельная полезность воды на самом деле низкая. Другими словами, каждую дополнительную единицу воды, которая становится доступной, можно использовать в менее критических целях, так как основная потребность воды (для выживания) удовлетворена.
Поэтому, любая отдельная единица воды теряет свою ценность из-за того, что в мире есть огромное её количество. С другой стороны бриллиантов в мире очень мало. Их настолько мало, что польза от одного бриллианта во много раз превышает пользу стакана воды, которой в мире очень много. Таким образом, бриллианты обладают гораздо большей ценностью для людей. Поэтому, те люди, которые хотят получить бриллианты согласны платить за них гораздо большую цену, чем за стакан воды, а продавцы бриллиантов устанавливают на каждый бриллиант стоимость, которая намного превышает стоимость стакана воды.
2. Парадокс убитого дедушки: Что было бы, если бы вы отправились назад во времени и убили вашего дедушку до того, как он встретил вашу бабушку?
Парадокс убитого дедушки является предложенным парадоксом путешествия во времени, который впервые был описан писателем в жанре научной фантастике Рене Баржавелем (René Barjavel) в его книге, опубликованной в 1943 году под названием «Неосторожный путешественник» (Le Voyageur Imprudent).
Предполагая наличие причинно-следственной связи между настоящим и будущим путешественника во времени, парадокс убитого дедушки, который нарушает эту связь, может рассматриваться как невозможный (таким образом, предотвращая самовольную переделку чьей-то судьбы). Тем не менее, для избегания парадокса был теоретически допущен ряд гипотез, таких как идея о том, что прошлое нельзя изменить, поэтому дедушка, должно быть, пережил попытку его убийства (как было заявлено ранее). Другая гипотеза состоит в том, что путешественник во времени создаёт или попадает в альтернативную временную линию или параллельную вселенную, в которой сам путешественник никогда не родился.
3. Парадокс Тесея: «Если все части корабля были заменены, остаётся ли корабль тем же кораблём?»
Корабль Тесея (Theseus) это парадокс, который поднимает следующий вопрос: остаётся ли предмет, в котором заменили все составные части, по сути, тем же предметом?
Этот парадокс обсуждался древними философами, и не так давно Томасом Гоббсом (Thomas Hobbes) и Джоном Локком (John Locke). Некоторые говорят: «корабль останется тем же», в то время как другие говорят, что «он не останется прежним».
Основываясь на истории можно сделать вывод, что то тело, которое мы видим в зеркале, является абсолютно другим телом по сравнению с тем, что мы видели семь лет назад или ранее, так как клетки человеческого тела регенерируются примерно каждые семь лет.
4. Парадокс Галилея: Хотя не все числа являются квадратами натуральных чисел, существует не больше натуральных чисел, чем квадратов натуральных чисел
Парадокс Галилея является демонстрацией одного из удивительных свойств бесконечных множеств. В своей последней научной работе «Две Науки» (Two New Sciences), он, по-видимому, сделал два противоречащих друг другу суждения о натуральных числах.
Первое состоит в том, что некоторые числа являются квадратами, в то время как другие числа ими не являются. Таким образом, всех чисел, включая квадраты и не квадраты, должно быть больше чем просто квадратов. Тем не менее, для каждого квадрата существует одно положительное число, которое является его квадратным корнем, и для каждого положительного числа существует только один квадрат, соответственно, одних не может быть больше, чем других. Это раннее использование, хотя и не первое, идеи о взаимно однозначном соответствии в контексте бесконечного множества. Галилей пришел к выводу, что идеи меньшего, равного, большего относятся к ограниченным, а не бесконечным множествам.
В девятнадцатом веке, используя те же методы, немецкий математик Георг Кантор (Georg Cantor), который лучше всего известен как изобретатель теории множеств, доказал, что это ограничение не является обязательным. Он показал, что можно значимым способом определить сравнения среди бесконечных множеств (исходя из чего два множества, которые он берёт в расчёт, складывает и возводит в квадрат, обладают «одинаковым размером»), и в соответствии с этим определением, некоторые множества являются строго большими, чем другие. Тем не менее, удивительно насколько Галилей забежал вперёд в своей более поздней работе по бесконечным числам. Он показал, что количество точек на отрезке прямой равно количеству точек на более крупном отрезке линии, но ему не удалось обнаружить доказательства Кантора, заключающегося в том, что эти количества больше, чем целые числа.
5. Парадокс бережливости: Если все попытаются экономить во время рецессии, совокупный спрос упадет, и общая сумма сэкономленная населением будет меньше
Парадокс бережливости состоит в том, что если все попытаются сэкономить деньги во время экономической рецессии, совокупный спрос упадёт и, в свою очередь, снизит общую сумму, сэкономленную населением, из-за снижения спроса в потреблении и в экономическом росте. Проще говоря, парадокс бережливости, заключается в следующем: общая сумма сэкономленная населением будет меньше, даже в том случае, когда индивидуальные сбережения увеличатся. В более широком смысле, это увеличение индивидуальных сэкономленных сбережений может быть вредоносным для экономики, так как, несмотря на то, что индивидуальная бережливость по общему утверждению является положительной для экономики, в соответствии с парадоксом бережливости – коллективная бережливость может оказать негативное воздействие на экономику. Теоретически, если все люди будут экономить свои сбережения, их объёмы увеличатся, но будет наблюдаться тенденция спада в макроэкономическом статусе.
6. Парадокс Пиноккио: Что было бы, если бы Пиноккио сказал: «Мой нос сейчас растёт»?
Парадокс Пиноккио наступает тогда, когда Пиноккио говорит «Мой нос сейчас растёт». Этот парадокс также является версией парадокса лжеца.
Парадокс лжеца определён в философии и логики как утверждение «Данное высказывание — ложь». Любые попытки придать этому утверждению классическое двоичное значение истинности приведут к противоречию, или парадоксу. Это происходит потому, что если утверждение «Данное высказывание — ложь» является правдой, тогда оно ложно. Это означает, что формально оно правдиво, но оно также и ложно, и так далее по замкнутому кругу.
Несмотря на то, что парадокс Пиноккио относится к лучшим традициям парадокса лжеца, он является особым случаем, так как у него нет семантических предикатов, например, как в случае утверждения «Данное высказывание — ложь».
Парадокс Пиноккио заключается не в том, что Пиноккио является известным лжецом. Если бы Пиноккио сказал «Я заболеваю», это могло бы быть правдой или ложью, однако предложение Пиноккио «Мой нос сейчас растёт» не может быть ни правдой, ни ложью. Именно поэтому только лишь это предложение создаёт парадокс Пиноккио.
7. Парадокс брадобрея: В деревне, где брадобрей бреет всех тех, кто не бреется сам, кто бреет брадобрея?
Представьте, что однажды вы проходите мимо парикмахерской и видите вывеску, на которой написано следующее: «Вы бреетесь самостоятельно? Если нет, заходите и я побрею вас! Я брею всех, кто не бреется сам, и никого другого». Это звучит вполне справедливо и довольно понятно, пока вам не придёт в голову следующий вопрос: «А бреет ли брадобрей самого себя?» Если он это делает, то он не должен этого делать, потому что он не бреет тех, кто бреется самостоятельно. Однако если он не бреется самостоятельно, он должен это делать, так как он бреет всех тех, кто не бреется самостоятельно и так далее по замкнутому кругу. Обе вероятности ведут к противоречию.
В этом заключается парадокс брадобрея, который был введён математиком, философом и человеком, отказавшимся исполнять воинскую повинность из Великобритании, по имени Бертран Рассел (Bertrand Russell) в начале двадцатого века. Этот парадокс представил собой огромную задачу, которая изменила всё направление математиков двадцатого века.
В парадоксе брадобрея условием является «бритьё самого себя», но множество всех мужчин, которые бреются самостоятельно невозможно подсчитать, несмотря на то, что это условие кажется вполне понятным. Мы не может подсчитать это множество, потому что мы не может решить входит ли сам брадобрей в него или нет. Оба условия ведут к противоречию.
Попытки обойти парадокс были сосредоточены на ограничении типов множеств, которые допустимы. Сам Рассел предложил «Теорию Типов» (Theory of Types), согласно которой, предложения должны были быть расположены в иерархическом порядке. На самом нижнем уровне должны быть предложения о множествах индивидуумов, на следующем уровне – предложения о множествах индивидуумов и так далее. Это помогает избежать необходимости обсуждения множества множеств, которые не являются членами самих себя, так как две части предложения являются разными типами и соответственно находятся на разных уровнях.
Ещё одно возможное (сексистское) решение парадокса заключается в следующем: просто сделайте брадобрея женщиной.
8. Парадокс дней рождения: Как в такой маленькой группе могут быть два человека, родившихся в один день?
Парадокс дней рождения состоит в вероятности того, что во множестве случайно выбранных людей, будут два человека, родившихся в один и тот же день. Согласно принципу Дирихле (pigeonhole principle), эта вероятность достигает 100 процентов, когда количество людей достигает 367 (исходя из того, что существует 366 возможных вариантов дат дней рождения, включая 29 февраля). Тем не менее, вероятность в 99 процентов, достигается, когда множество состоит всего лишь из 57 людей, и 50 процентов, если было собрано 23 человека. Эти выводы включают предположение, что каждый день в году (кроме 29 февраля) в равной степени является вероятной датой дня рождения.
9. Проблема курицы и яйца: Что было раньше — курица или яйцо?
Причинно-следственная дилемма курицы или яйца зачастую звучит как «Что было раньше — курица или яйцо?». Для древних философов вопрос о том, что появилось первым курица или яйцо, также означал ряд вопросов о том, как появилась жизнь во Вселенной и как она началась в целом.
Культурные отсылки к парадоксу курицы или яйца обычно делаются, чтобы указать на бесполезность стремления установить первый случай круговой причины и последствия. Можно предположить, что в этом подходе лежит основополагающая природа вопроса. Буквальный ответ довольно очевиден некоторым людям, так как яйцекладущие виды появились раньше кур. Другие же полагают, что вначале появилась курица, так как куры являются всего лишь одомашненными Банкивскими джунглевыми курами (Red Junglefowls). Однако метафорический взгляд на этот парадокс обуславливает метафизическое основание дилеммы. Чтобы лучше понять её метафорическое значение, вопрос можно переформулировать следующим образом: «Что появилось раньше, Х, который не может существовать без Y, или же Y, который не может существовать без Х?». Когда много лет назад появилась Земля, появилась и курица. Затем она отложила яйцо. Если бы яйцо появилось первым, и из него вылупился бы цыплёнок, кто бы его согревал, и кто бы его кормил?
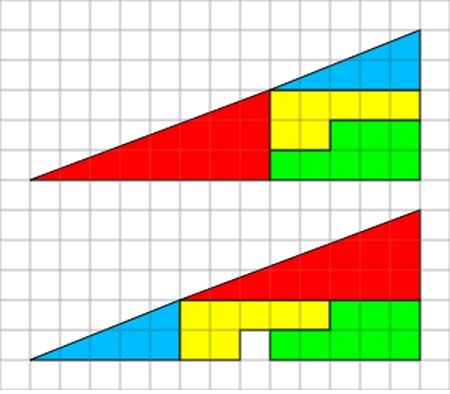
10. Исчезновение клетки: Почему квадрат появляется без видимой причины?
Парадокс исчезновения клетки это оптическая иллюзия, используемая на математических лекциях, чтобы помочь студентам понять геометрические фигуры. Он состоит в описании двух расположений фигурок, состоящих из похожих форм, немного разной конфигурации.
Ключом к головоломке является тот факт, что ни один из «треугольников» не является настоящим треугольником, из-за изогнутой гипотенузы. Другими словами «гипотенуза» не является совместимой наклонной, несмотря на то, что она может казаться такой невооружённому человеческому глазу. Поэтому, в то время как изогнутая гипотенуза на первом рисунке на самом деле занимает 32 клетки, на втором рисунке, она занимает 33 клетки, включая «исчезающую» клетку. Обратите внимание на точку сети, где соприкасаются красный и синий треугольники на нижнем изображении (5 клеточек вправо и две клеточки вверх от левого нижнего угла комбинированной фигуры), и сравните это с той же точкой на верхнем изображении. Край немного не достаёт до отметки на верхнем изображении, но переходит через неё на нижнем. В результате наложения гипотенуз обеих фигур друг на друга получается очень узкий параллелограмм, площадь которого точно равна площади клетки «исчезнувшей» на нижнем изображении.
Поддержи Бугага.ру и поделись этим постом с друзьями! Спасибо! 🙂