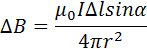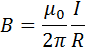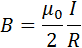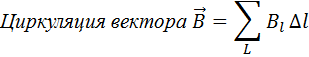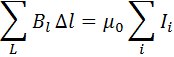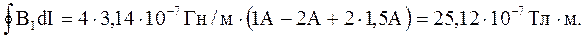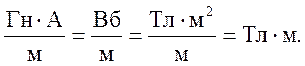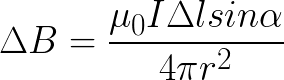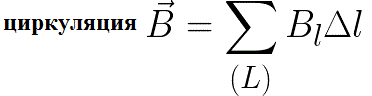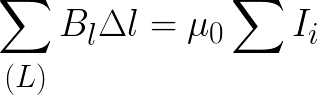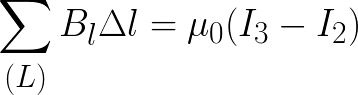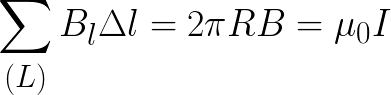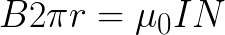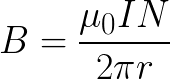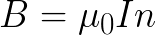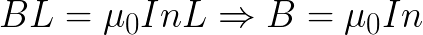Закон Био-Савара. Теорема о циркуляции

Магнитное поле постоянных токов различной конфигурации изучалось экспериментально французскими учеными Жан Батист Био и Феликсом Саваром (1820 г.). Они пришли к выводу, что индукция магнитного поля токов, текущих по проводнику, определяется совместным действием всех отдельных участков проводника. Магнитное поле подчиняется принципу суперпозиции:

Если магнитное поле создается несколькими проводниками с током, то индукция результирующего поля есть векторная сумма индукций полей, создаваемых каждым проводником в отдельности.

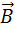
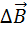
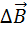
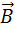
Индукцию проводника с током можно представить как векторную сумму элементарных индукций создаваемых отдельными участками проводника. На опыте невозможно выделить отдельный участок проводника с током, так как постоянные токи всегда замкнуты. Можно измерить только суммарную индукцию магнитного поля, создаваемого всеми элементами тока. Закон Био–Савара определяет вклад в магнитную индукцию результирующего магнитного поля, создаваемый малым участком Δl проводника с током I.

Здесь r – расстояние от данного участка Δl до точки наблюдения, α – угол между направлением на точку наблюдения и направлением тока на данном участке, μ₀ – магнитная постоянная. Направление вектора 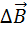определяется правилом буравчика: оно совпадает с направлением вращения рукоятки буравчика при его поступательном перемещении вдоль тока. Рис. 1.17.1 иллюстрирует закон Био–Савара на примере магнитного поля прямолинейного проводника с током. Если просуммировать (проинтегрировать) вклады в магнитное поле всех отдельных участков прямолинейного проводника с током, то получится формула для магнитной индукции поля прямого тока:

которая уже приводилась в 1.16.

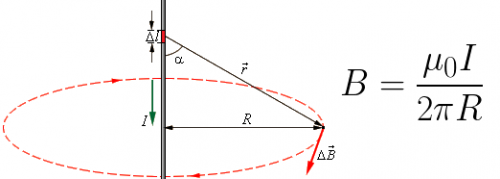
Иллюстрация закона Био–Савара

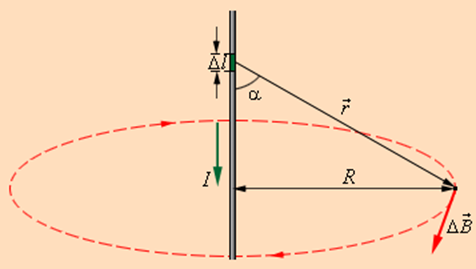
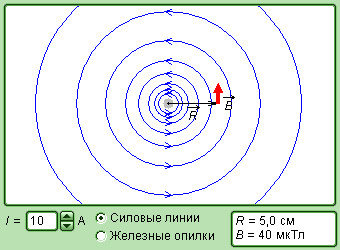
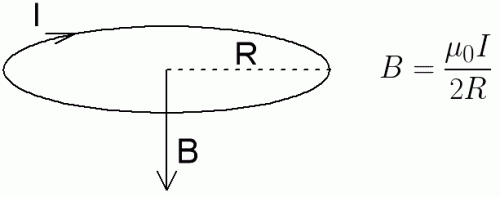
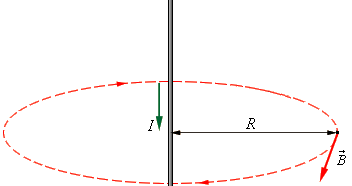
Закон Био–Савара позволяет рассчитывать магнитные поля токов различных конфигураций. Нетрудно, например, выполнить расчет магнитного поля в центре кругового витка с током. Этот расчет приводит к формуле

где R – радиус кругового проводника. Для определения направления вектора 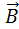также можно использовать правило буравчика, только теперь его рукоятку нужно вращать в направлении кругового тока, а поступательное перемещение буравчика укажет направление вектора магнитной индукции.

Расчеты магнитного поля часто упрощаются при учете симметрии в конфигурации токов, создающих поле. В этом случае можно пользоваться теоремой о циркуляции вектора магнитной индукции, которая в теории магнитного поля токов играет ту же роль, что и теорема Гаусса в электростатике.

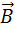
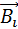
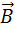
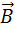
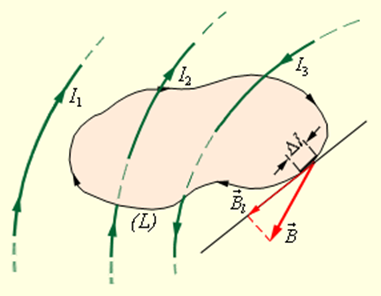
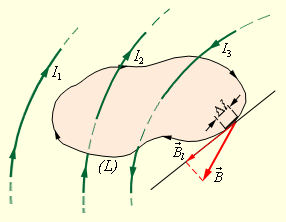
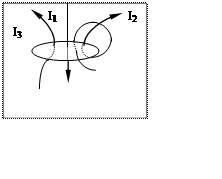
Поясним понятие циркуляции вектора Пусть в пространстве, где создано магнитное поле, выбран некоторый условный замкнутый контур (не обязательно плоский) и указано положительное направление его обхода. На каждом отдельном малом участке Δl этого контура можно определить касательную составляющую вектора в данном месте, то есть определить проекцию вектора на направление касательной к данному участку контура (рис. 1.17.2).

Замкнутый контур (L) с заданным направлением обхода. Изображены токи I₁, I₂ и I₃, создающие магнитное поле

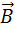
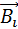
Циркуляцией вектора называют сумму произведений Δl, взятую по всему контуру L:

Некоторые токи, создающие магнитное поле, могут пронизывать выбранный контур L в то время, как другие токи могут находиться в стороне от контура.

Теорема о циркуляции утверждает, что циркуляция вектора 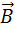магнитного поля постоянных токов по любому контуру L всегда равна произведению магнитной постоянной μ₀ на сумму всех токов, пронизывающих контур:

В качестве примера на рис. 1.17.2 изображены несколько проводников с токами, создающими магнитное поле. Токи I₂ и I₃ пронизывают контур L в противоположных направлениях, им должны быть приписаны разные знаки – положительными считаются токи, которые связаны с выбранным направлением обхода контура правилом правого винта (буравчика). Следовательно, I₃ > 0, а I₂ Опубликовано в разделах: Электродинамика, Магнитное поле

Источник

Закон Био-Савара. Теорема о циркуляции

Принцип суперпозиции: если магнитное поле работает за счет нескольких проводников с током, тогда индукция результативного поля – это совокупность индукций полей, которые создаются каждым проводником по отдельности.

Индукция B → проводника с током представлена, как векторная сумма элементарных индукций ∆ B → вырабатываемых отдельными участками проводника. На практике нельзя отделить один участок проводника с током, поскольку постоянные токи всегда замкнутые. Возможно лишь измерить совокупную индукцию магнитного поля, которое создают все элементы тока. Как найти индукцию магнитного поля?

Закон Био–Савара

В формуле r – это расстояние от заданного участка Δ l до точки наблюдения, α – это угол между направлением на точку наблюдения и направлением тока на заданном участке, μ 0 – это магнитная постоянная.

С помощью этого закона можно определять магнитные поля токов с различными конфигурациями. Запросто рассчитать магнитное поле в центре кругового витка с током. Вычисления приводят к соотношению:

где R – это радиус кругового проводника.

Чтобы определить направление вектора B → тоже используется правило буравчика, только в этом случае рукоятка вращается по направлению кругового тока, а поступательное движение буравчика указывает, куда направлен вектор магнитной индукции.

Теорема о циркуляции вектора магнитной индукции

Вычисления магнитного поля зачастую упрощаются с учетом симметрии в конфигурации токов. В этом помогает теорема о циркуляции вектора магнитной индукции.

Некоторые токи, при которых магнитное поле создается, пропускают выбранный контур L тем временем, как остальные токи находятся в стороне от контура.

Согласно теореме о циркуляции, циркуляция вектора B → магнитного поля постоянных токов по любому из контуров L все время определяется, как произведение магнитной постоянной μ 0 на сумму всех токов:

∑ ( L ) B l ∆ l = μ 0 ∑ l i.

Теорема о циркуляции в этом примере математически выражается следующей формулой:

Общий вид теоремы о циркуляции можно вывести из принципа суперпозиции и закона Био-Савара.

отсюда можно вывести формулу для модуля магнитной индукции поля прямолинейного проводника с током, приведенную раньше.

Из данного примера видно, что теорема о циркуляции вектора магнитной индукции B → можно использовать для вычисления магнитных полей, которые создаются симметричным распределением токов, когда можно наугад определить общую структуру поля.

Существует много примеров определения магнитных полей при помощи теоремы о циркуляции.

Предположим, что катушка намотана виток к витку на ненамагниченный тороидальный сердечник. В ней линии магнитной индукции сходятся внутри катушки и выступают концентрическими окружностями. Они имеет такое направление, что, смотря вдоль них, наблюдатель увидел бы ток в витках, циркулирующих по часовой стрелке.

Однако в пределе каждая часть тороидальной катушки при необходимости рассматривается в качестве длинной прямолинейной катушки, которая называется соленоид. Вдали торцов такой катушки модуль магнитной индукции определяется, как соотношение в случае с тороидальной катушкой.

Данное вычисление совпадает с формулой для магнитного поля тонкой тороидальной катушки.

Источник

В = = .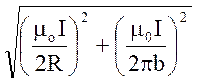

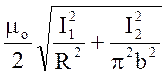
Подставляя числовые данные задачи, получим:

2. МАГНИТНЫЙ ПОТОК, ПОТОКОСЦЕПЛЕНИЕ.

ТЕОРЕМА ГАУССА И ТЕОРЕМА О ЦИРКУЛЯЦИИ ВЕКТОРА В

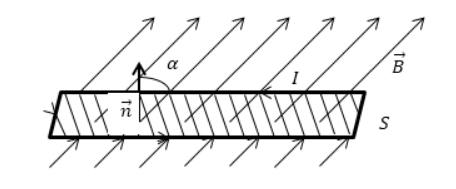
Поток магнитной индукции Ф_м через некоторую поверхность S

Пример. Виток радиусом 2 см расположен в однородном магнитном поле с индукцией В = 2 мТл так, что его плоскость составляет 30 0 с силовыми линиями. Найти магнитный поток через виток.

Так как линии вектора В всегда замкнуты, то число линий, выходящих из объема V, равно количеству линий, входящих в него. Поэтому поток вектора В через любую замкнутую поверхность равен нулю:

Ф_в = 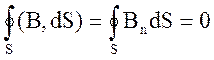(3.2.2)

В этом состоит смысл теоремы Гаусса для магнитного поля.

Если контур состоит из N витков, каждый из которых пронизывается магнитным потоком Ф, алгебраическая сумма потоков

Величина Ψ называется потокосцеплением или полным магнитным потоком, измеряется так же, как и магнитный поток, в веберах.

Теорема о циркуляции вектора магнитной индукции утверждает, что циркуляция вектора В вдоль замкнутого контура в отсутствие переменных электрических полей равна алгебраической сумме токов, охватываемых контуром:

( 3.2.3)

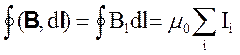
Значение силы тока берут со знаком «плюс», если направление тока и направление обхода контура составляет правовинтовую систему, и со знаком « минус», если левовинтовую. Выбор направления обхода произволен. Если ток охватывает контур N раз, то это обстоятельство учитывают произведением NI.

Пример. На рис.8 изображен произвольный контур, охватывающий несколько проводников с токами. Токи равны: I₁ = 1 A; I₂ = 2 A; I₃ = 1,5 A. Найти циркуляцию вектора магнитной индукции вдоль этого контура.

Решение. Согласно формуле (3.2.3). циркуляция вектора В имеет вид

Проведем операции с размерностями и покажем, что циркуляция измеряется в Тл·м:

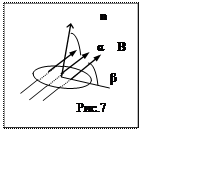Ниже будет показано, что произведение индуктивности и тока дает потокосцепление (L·I = Ψ), отсюда Гн·А = Вб.

Из формулы (3.2.3), как следствие, вытекает формула для расчета магнитной индукции поля на оси бесконечно длинного соленоида в его середине:

(3.2.4)

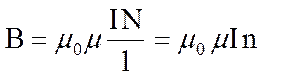
где N – общее число соленоида; l – его длина ; n = N /l– число витков на единицу длины, μ – магнитная проницаемость сердечника, (если сердечника нет или он немагнитный, то μ =1).

3. ДЕЙСТВИЕ МАГНИТНОГО ПОЛЯ НА ДВИЖУЩИЕСЯ

ЗАРЯДЫ И ПРОВОДНИКИ С ТОКОМ. РАБОТА СИЛ ПОЛЯ

Рассмотрим последовательно, как магнитное поле действует сначала на движущиеся заряды, затем на проводники с токами, в том числе и на рамку с током. В общем случае электромагнитное поле характеризуется векторами Е(r,t) – напряженностью электрического поля и В(r,t) – магнитной индукцией. Сила, действующая на заряженную частицу, движущуюся в электромагнитном поле,

называется силой Лоренца. Квадратные скобки означают векторное произведение двух векторов v и B.

Выражение (3.3.1) справедливо как для постоянных, так и переменных электромагнитных полей. С магнитным полем связана та часть силы, которая проявляется только при движении заряда (см. второе слагаемое в выражении (3.3.1)), т.е.

Источник

Закон Био-Савара и теорема о циркуляции вектора магнитной индукции

В 1820 году, французские ученые Жан Батист Био и Феликс Савар, в ходе совместного проведения экспериментов по изучению магнитных полей постоянных токов, однозначно установили, что магнитную индукцию текущего по проводнику постоянного тока можно считать результатом общего действия всех участков данного проводника с током. Это значит, что магнитное поле подчиняется принципу суперпозиции (принципу наложения полей).

Магнитное поле, созданное группой проводников с постоянным током, имеет такую магнитную индукцию, что ее величина определяется как векторная сумма магнитных индукций, создаваемых каждым проводником индивидуально. То есть, индукцию В проводника с постоянным током можно справедливо представить векторной суммой элементарных индукций dB, принадлежащих элементарным участкам dl рассматриваемого проводника с постоянным током I.

Практически нереально выделить элементарный участок проводника с постоянным током, ведь постоянный ток всегда замкнут. Но можно измерить общую магнитную индукцию, создаваемую проводником, то есть порождаемую всеми элементарными кусочками данного проводника.

Таким образом, Закон Био-Совара позволяет найти величину магнитной индукции В от участка (известной длины dl) проводника, с заданным постоянным током I, на определенном расстоянии r от этого участка проводника и в определенном направлении наблюдения от выбранного участка (задается через синус угла между направлением тока и направлением от участка проводника к исследуемой точке пространства около проводника):

Экспериментально установлено, что направление вектора магнитной индукции с легкостью определяется правилом правого винта или буравчика: если направление поступательного движения буравчика при его вращении совпадает с направлением постоянного тока I в проводнике, то направление вращения рукоятки буравчика определяет направление вектора магнитной индукции B, получаемой от данного тока.

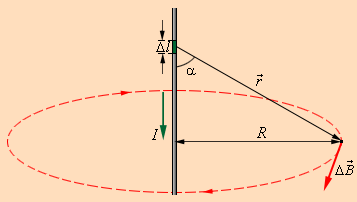
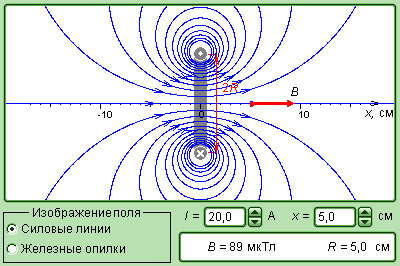
Магнитное поле прямолинейного проводника с током, а также иллюстрация применения закона Био-Савара к нему, представлены на рисунке:

Итак, если проинтегрировать, то есть сложить, вклады каждого из маленьких участков прямого проводника с постоянным током в общее магнитное поле, то получится формула для нахождения индукции магнитного поля проводника с током на определенном радиусе R от него.

Таким же образом, при помощи закона Био-Савара, можно рассчитывать магнитные индукции от постоянных токов разнообразных конфигураций и в определенных точках пространства, например магнитная индукция в центре круглого витка с током находится по следующей формуле:

Направление вектора магнитной индукции легко находится по правилу буравчика, только теперь буравчик нужно вращать по направлению замкнутого тока, а поступательное движение буравчика покажет направление вектора магнитной индукции.

Часто расчеты касательно магнитного поля можно упростить, если принять во внимание симметрию конфигурации токов, данное поле порождающих. Здесь можно пользоваться теоремой о циркуляции вектора магнитной индукции (как теорема Гаусса в электростатике). Что такое «циркуляция вектора магнитной индукции»?

Выберем в пространстве некий замкнутый контур произвольной формы, и укажем условно положительное направление его обхода. Для каждой точки данного контура можно найти проекцию вектора магнитной индукции В на касательную к контуру в данной точке. Тогда сумма произведений данных величин на элементарные длины всех участков контура — это и будет циркуляция вектора магнитной индукции В по данному контуру:

Практически, все токи, создающие здесь суммарное магнитное поле, могут либо пронизывать рассматриваемый контур, либо некоторые из них могут быть за его пределами. Согласно теореме о циркуляции: циркуляция вектора магнитной индукции В постоянных токов по замкнутому контуру численно равна произведению магнитной постоянной мю0 на сумму всех постоянных токов, данный контур пронизывающих. Эту теорему сформулировал Андре Мари Ампер в 1826 году:

Рассмотрим приведенный выше рисунок. Здесь токи I1 и I2 пронизывают контур, но направлены они в разные стороны, значит имеют условно разные знаки. Положительный знак будет иметь тот ток, направление магнитной индукции у которого (по правилу буравчика) совпадает с направлением обхода выбранного контура. Для данной ситуации теорема о циркуляции примет вид:

В общем виде теорема о циркуляции вектора магнитной индукции B следует из принципа суперпозиции магнитного поля и закона Био-Савара.

Для примера выведем формулу для магнитной индукции прямого проводника с постоянным током. Выберем контур в форме окружности, сквозь центр которой проходит данный проводник, причем проводник перпендикулярен плоскости контура.

Таким образом, центр окружности лежит прямо по центру проводника, то есть в проводнике. Поскольку картина симметричная, то вектор В направлен по касательной к окружности, и его проекция на касательную, соответственно, везде одна и та же и равна длине самого вектора В. Теорема о циркуляции запишется так:

Отсюда и следует формула для магнитной индукции прямолинейного проводника с постоянным током (данная формула уже была приведена выше). Подобным образом с помощью теоремы о циркуляции можно легко находить магнитные индукции симметричных конфигураций постоянных токов, где картина силовых линий представляется легко.

Одним из практически важных примеров применения теоремы о циркуляции является нахождение магнитного поля внутри тороидальной катушки индуктивности.

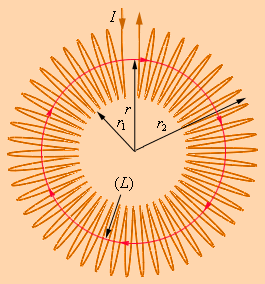
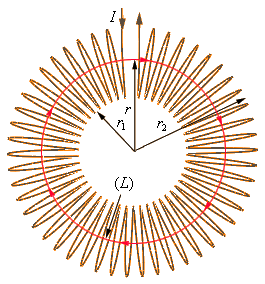
Допустим, имеется тороидальная катушка, намотанная виток к витку на картонный каркас в форме бублика, с числом витков N. Линии магнитной индукции при такой конфигурации замыкаются внутри бублика и по форме представляют собой концентрические (одна в другой) окружности.

Если смотреть вдоль по направлению вектора магнитной индукции на внутренней оси бублика, то окажется, что ток направлен везде по часовой стрелке (в соответствии с правилом буравчика). Рассмотрим одну из линий (показана красным цветом) магнитной индукции внутри катушки, и выберем ее в качестве круглого контура радиусом r. Тогда теорема о циркуляции для данного контура запишется так:

И магнитная индукция поля внутри катушки будет равна:

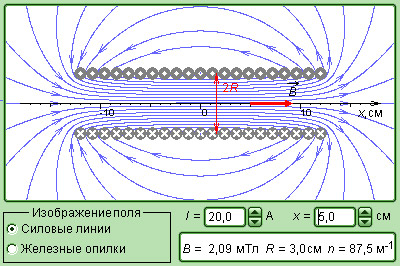
Для тонкой тороидальной катушки, где магнитное поле практически однородно по всему ее сечению, можно записать выражение магнитной индукции словно для бесконечно длинного соленоида с учетом числа витков на единицу длины — n:

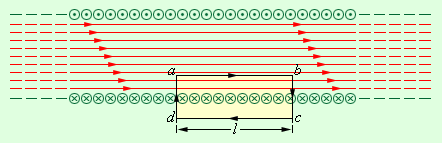
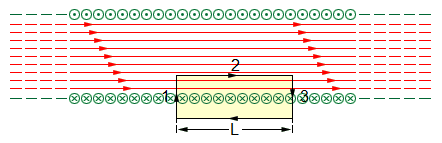
Рассмотрим теперь бесконечно длинный соленоид, где магнитное поле полностью находится внутри. Применим теорему о циркуляции к выбранному прямоугольному контуру.

Если Вам понравилась эта статья, поделитесь ссылкой на неё в социальных сетях. Это сильно поможет развитию нашего сайта!

Подписывайтесь на наш канал в Telegram!

Просто пройдите по ссылке и подключитесь к каналу.

Не пропустите обновления, подпишитесь на наши соцсети:

Источник

Поток вектора магнитной индукции

Магнитный поток Φ через площадку S (поток вектора магнитной индукции) – это скалярная величина:

Формула магнитного потока

В чем измеряется магнитный поток

Нахождение полного потока через поверхность S :

Связь магнитного потока и работы сил магнитного поля

Если проводник с током совершает конечное перемещение, сила тока постоянна, то работа сил поля равняется:

Теорема Гаусса для магнитного поля

Значение суммарного магнитного потока через замкнутую поверхность S равняется нулю:

Выражение ∮ B → d S → = 0 является справедливым для любых магнитных полей. Данное уравнение считается аналогом теоремы Остроградского-Гаусса в электростатике в вакууме:

Запись ∮ B → d S → = 0 говорит о том, что источник магнитного поля – это не магнитные заряды, а электрические токи.

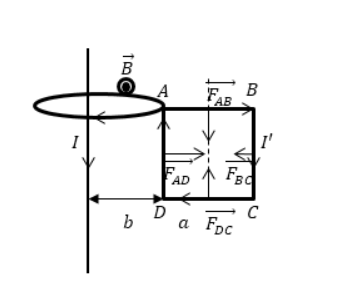
Индукция магнитного поля длинного проводника с током в части, где расположена квадратная рамка, направляется на нас.

Следует учитывать нахождение рамки с током в неоднородном поле, что означает убывание магнитной индукции при удалении от провода.

За основу возьмем формулу магнитного потока и работы, которая их связывает:

Найти силу, действующую на рамку, из предыдущего примера.

Элементарная работа δ A может быть выражена как:

Используем выражение, которое было получено в примере 1 :

Каждый элемент контура квадратной рамки находится под воздействием сил (силы Ампера). Отсюда следует, что на рамку действует 4 силы, причем на стороны A B и D C равные по модулю и противоположные по направлению. Выражение принимает вид:

Используя правило левой руки, получаем направление этих сил вдоль одной прямой в противоположные стороны:

Значение F B C будет:

Для нахождения искомой силы:

Источник