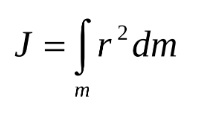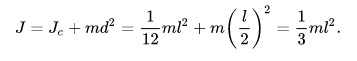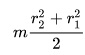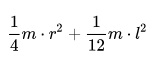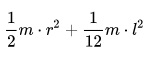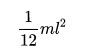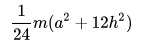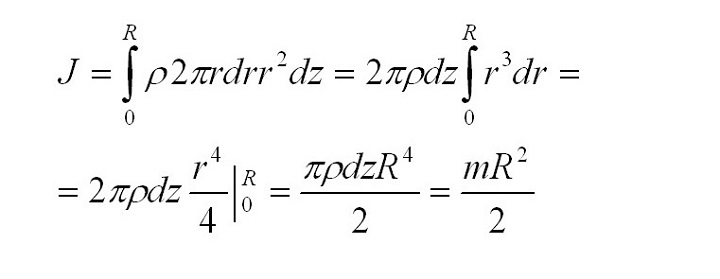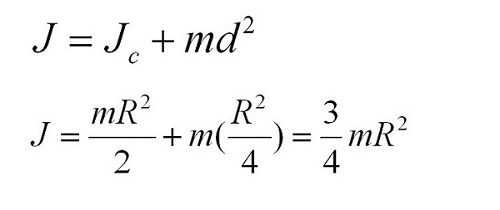момент инерции полой сферы

Момент инерции для чайников: определение, формулы, примеры решения задач

Часто мы слышим выражения: «он инертный», «двигаться по инерции», «момент инерции». В переносном значении слово «инерция» может трактоваться как отсутствие инициативы и действий. Нас же интересует прямое значение.

Ежедневная рассылка с полезной информацией для студентов всех направлений – на нашем телеграм-канале.

Что такое инерция

Согласно определению инерция в физике – это способность тел сохранять состояние покоя или движения в отсутствие действия внешних сил.

Если с самим понятием инерции все понятно на интуитивном уровне, то момент инерции – отдельный вопрос. Согласитесь, сложно представить в уме, что это такое. В этой статье Вы научитесь решать базовые задачи на тему «Момент инерции».

Определение момента инерции

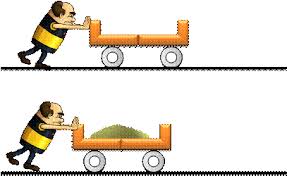
Из школьного курса известно, что масса – мера инертности тела. Если мы толкнем две тележки разной массы, то остановить сложнее будет ту, которая тяжелее. То есть чем больше масса, тем большее внешнее воздействие необходимо, чтобы изменить движение тела. Рассмотренное относится к поступательному движению, когда тележка из примера движется по прямой.

По аналогии с массой и поступательным движением момент инерции – это мера инертности тела при вращательном движении вокруг оси.

Момент инерции – скалярная физическая величина, мера инертности тела при вращении вокруг оси. Обозначается буквой J и в системе СИ измеряется в килограммах, умноженных на квадратный метр.

Как посчитать момент инерции? Есть общая формула, по которой в физике вычисляется момент инерции любого тела. Если тело разбить на бесконечно малые кусочки массой dm, то момент инерции будет равен сумме произведений этих элементарных масс на квадрат расстояния до оси вращения.

Это общая формула для момента инерции в физике. Для материальной точки массы m, вращающейся вокруг оси на расстоянии r от нее, данная формула принимает вид:

Теорема Штейнера

От чего зависит момент инерции? От массы, положения оси вращения, формы и размеров тела.

Теорема Гюйгенса-Штейнера – очень важная теорема, которую часто используют при решении задач.

Кстати! Для наших читателей сейчас действует скидка 10% на любой вид работы

Теорема Гюйгенса-Штейнера гласит:

Момент инерции тела относительно произвольной оси равняется сумме момента инерции тела относительно оси, проходящей через центр масс параллельно произвольной оси и произведения массы тела на квадрат расстояния между осями.

Для тех, кто не хочет постоянно интегрировать при решении задач на нахождение момента инерции, приведем рисунок с указанием моментов инерции некоторых однородных тел, которые часто встречаются в задачах:

Пример решения задачи на нахождение момента инерции

Рассмотрим два примера. Первая задача – на нахождение момента инерции. Вторая задача – на использование теоремы Гюйгенса-Штейнера.

Задача 1. Найти момент инерции однородного диска массы m и радиуса R. Ось вращения проходит через центр диска.

Разобьем диск на бесконечно тонкие кольца, радиус которых меняется от 0 до R и рассмотрим одно такое кольцо. Пусть его радиус – r, а масса – dm. Тогда момент инерции кольца:

Массу кольца можно представить в виде:

Здесь dz – высота кольца. Подставим массу в формулу для момента инерции и проинтегрируем:

В итоге получилась формула для момента инерции абсолютного тонкого диска или цилиндра.

Задача 2. Пусть опять есть диск массы m и радиуса R. Теперь нужно найти момент инерции диска относительно оси, проходящей через середину одного из его радиусов.

Момент инерции диска относительно оси, проходящей через центр масс, известен из предыдущей задачи. Применим теорему Штейнера и найдем:

Кстати, в нашем блоге Вы можете найти и другие полезные материалы по физике и решению задач.

Надеемся, что Вы найдете в статье что-то полезное для себя. Если в процессе расчета тензора инерции возникают трудности, не забывайте о студенческом сервисе. Наши специалисты проконсультируют по любому вопросу и помогут решить задачу в считанные минуты.

Источник

Физический смысл момента инерции

Обновлено: 16 Июля 2021

Когда тело продолжает двигаться при отсутствии на него воздействия каких-либо сил, говорят о проявлении инерции. Именно ею объясняются трудности удержаться на ногах при резком торможении автобуса или усидеть в седле велосипеда, когда под колеса резко выбегает кот. Кроме инерции, проявляющейся при движении тел по прямой, аналогичное явление бывает при вращении вокруг оси. В таком случае в физике говорят о моменте инерции – скалярной величине, измеряющей инертность тела при осевом вращении.

Момент инерции и его физический смысл

Обеспечить поступательное движение предмета при его толкании будет тем тяжелее, чем больше он весит. Аналогичные эксперименты предусматривались школьной программой и относились к прямо направленному действию.

Было понятно, что именно масса тела характеризует степень его инертности и является ее мерой.

При совершении предметом вращательных движений наблюдается иной вид зависимости. В данном случае мерой инертности выступает момент инерции.

Момент инерции – скалярная измеряемая характеристика инертности тела в момент совершения осевого вращения.

Задачи по определению величины момента инерции решаются с помощью теоремы Гюйгенса-Штейнера, смысл которой заключается в следующем:

МИ для тела, вращающегося вокруг какой-либо оси, равна сумме слагаемых единиц: момент инерции предмета, который вращается вокруг оси, параллельной данной, и проходящей через центр масс, а также произведения массы на расстояние между осями, возведенное в квадрат.

В приведенной формуле используются следующие обозначения: d – расстояние между осями, m – масса тела, Iz – момент инерции относительно рассматриваемой оси, а Ic – относительно оси, которая проходит через центр масс. В профильной литературе и учебниках буква I может заменяться J.

Формулировка способа количественного измерения момента инерции при осевом вращении предмета стала возможной в результате работы двух ученых-математиков: Гюйгенса и Штейнера. Теорема дает возможность быстрого решения задач на определение инерции предмета любой формы, для которого уже просчитана центробежная сила. Формула Штейнера позволяет вычислить момент инерции этого предмета относительно выбранной оси, проходящей параллельно прямой, следующей через центр фигуры.

Единицы измерения в системе СИ

Как рассчитать момент инерции, формула

Измерение значения момента инерции можно произвести теоретически, согласно формуле. Для этого условно движущийся предмет разбивается на мелкие составляющие, масса которых обозначается dm. В конечном итоге момент инерции (МИ) равняется сумме произведений всех образовавшихся масс на расстояние до оси, возведенное в квадрат.

Исходя из этой формулы, момент инерции, кроме массы тела, определяется положением оси, вокруг которой предмет вращается, а также его формой и габаритами.

Возможность рассчитать моменты инерции полезна, к примеру, при исследованиях свойств и структуры элементов Солнечной системы. Это так называемый безразмерный момент инерции. Высчитанная по формуле величина дает представление о распределении массы по глубине.

Виды моментов инерции

Кроме безразмерного момента инерции, в физике существуют понятия:

Центробежными МИ относительно прямоугольных осей координат (декартовой системы) считаются Jxy, Jxz, Jyz. Ось ОХ является главной, когда центробежные моменты инерций Jxy и Jxz равняются нулям.

Для геометрических МИ существуют формулы, основывающиеся на объеме относительно оси и площади относительно оси.

Твердое тело может иметь МИ относительно плоскости. Тогда это – скалярная величина, которая рассчитывается суммированием произведений массы каждой точки предмета и расстояния от нее до плоскости, возведенного в квадрат.

Понятие «Центрального МИ» связано с точкой О, МИ относительно полюса либо полярным МИ.

Момент инерции тела относительно оси вращения

МИ служит единицей измерения инерции тела, которое вращается вокруг оси, подобно тому, как масса является мерой при поступательном движении.

Определить МИ предметов касательно оси вращения позволяет формула Штейнера.

Пример:

Наглядное подтверждение применения формулы Штейнера – расчет МИ стержня, ось вращения которого проходит через конец.

Моменты инерции простейших объектов

Момент инерции некоторых однородных тел, имеющих простую форму, в зависимости от характеристик осей вращения можно определить по следующим формулам:

Примеры решения задач

Применение на практике приведенных формул происходит, например, для решения следующих задач.

Пример №1

Задано найти МИ однородного диска с известными массой и радиусом. Из дополнительных сведений: ось вращения – через центр диска.

С учетом подстановки в конечную формулу для определения МИ формулы для массы кольца получаем:

Пример № 2

Задано найти у того же диска МИ относительно оси, которая проходит через середину радиуса.

Из предшествующего задания используем найденную величину МИ относительно оси, которая проходит через центр масс. Используя формулу Штейнера, решаем задачу.

Если решать аналогичные задачи нет желания или времени, а контрольную работу нужно сдать в срок, на помощь придут сотрудники Феникс.Хелп.

Источник

ИНЕРЦИЯ И МОМЕНТ ИНЕРЦИИ: базовые сведения

История понятия «инерция»

До эпохи Возрождения, в Средние века, в западной философии общепринятой была аристотелевская теория движения. Ученик Платона, древнегреческий философ Аристотель (384 – 322 гг. до н. э.) утверждал, что в отсутствии внешней силы все объекты остановятся, и что движущиеся объекты продолжают двигаться только до тех пор, пока есть побуждающая к движению сила.

Принцип движения по инерции, который возник у Аристотеля для «движений в пустоте», гласил, что объект имеет тенденцию сопротивляться изменению движения.

Окончательно от аристотелевской теории отказались в ходе ряда открытий, предшествовавших научной революции XVII века.

Термин «инерция», от латинского слова «безделье» или «лень» (лат. inertia), был впервые использован немецким математиком и астрономом Иоганном Кеплером (1571 – 1630 гг.) в его книге «Epitome Astronomiae Copernicanae», которая была опубликована в трех частях в 1617–1621 гг. Но Кеплер определял инерцию только как сопротивление движению, основываясь на старом предположении, что покой – это естественной состояние вещей, которое не нужно объяснять и к которому стремятся тела.

Покой и движение объединил единым принципом современник Кеплера Галилео Галилей (1564 — 1642) — итальянский физик, механик, астроном, философ и математик. Он первый, кто направил зрительную трубу в небо, превратив её в телескоп. В 1609 году он создал свой первый телескоп с трёхкратным увеличением. Галилео Галилей писал, что «если устранить все внешние препятствия, то тяжелое тело на сферической поверхности, концентрической Земле, будет поддерживать себя в том состоянии, в котором оно находилось; если его поместить в движение к западу (например), то оно будет поддерживать себя в этом движении».

Чтобы оспорить идею Аристотеля о естественности состояния покоя, Галилей проводил один из таких мысленных экспериментов. Если исключить силу трения, то шар, катящийся по склону оврага (холма), взлетит до той же высоты на противоположной стороне. Если второй склон постепенно наклонять, шар будет катиться все дальше и дальше и в горизонтальном положении склона будет катиться бесконечно долго.

Галилей сделал вывод, что «Тело, движущееся по ровной поверхности, будет продолжать движение в том же направлении с постоянной скоростью, если движение не будет нарушено».

Позднее, мысли Галилея будут уточнены и систематизированы Исааком Ньютоном. Исаак Ньютон (1642 – 1727) — английский физик, математик, механик и астроном, основатель классической физики. В своем труде «Математические начала натуральной философии» (Philosophiae Naturalis Principia Mathematica), впервые опубликованном в 1687 году, он изложил закон всемирного тяготения и три закона динамики.

Явление инерции, изначально сформулированное Галилеем, вошло в первый закон Ньютона.

Оговоримся, что согласно определению, законы Ньютона справедливы только для систем отсчета (система отсчета – это тело отсчета со связанной с ним системой координат, относительно которого можно вычислять положение тел, и система измерения времени, т.е. некоторые часы), которые принято называть инерциальными. Инерциальная система отсчета – это такая система, в которой ускорение тел зависит только от приложенных сил, а не свойством самой системы отсчета (наблюдателя) перемещаться с ускорением.

Посмотрим на второй закон Ньютона.

Чаще его записывают в виде:

так как в инерциальной системе отсчета сила является причиной ускорения тела.

Как видно из второй формулы, для тела неизменной массы ускорение тела (скорость изменения его скорости) прямо пропорционально силе, приложенной к телу (чем сильнее толкаем, тем быстрее тело разгоняется) и обратно пропорционально его массе (чем тяжелее тело, тем сложнее его разгонять).

Представим, что тело движется в вакууме и на него не действуют никакие силы (F=0). Значит и скорость его меняться не будет (a=0).

Инерция (лат. inertia — покой, постоянство, неизменность) – природное явление сохранения равномерного прямолинейного движения или состояния покоя любого тела, пока на него не действуют внешние силы или если действие сил скомпенсировано.

Инертность – свойство конкретного тела оставаться в покое или равномерно прямолинейно двигаться. От инертности зависит ускорение тела при приложении к нему внешних сил. Мерой количественного измерения инертности тела в прямолинейном движении является его масса. Больше масса – больше инертность тела, т.е. тем сложнее придать ему ускорение (разогнать или остановить).

Из-за большей чем у легковушки массы у грузовика инертность выше. Соответственно, и тормозной путь у него будет больше – нужно приложить большую силу, чтоб его остановить (хотя, можно поставить очень мощные тормоза). Говорить, что у грузовика больше инерция – некорректно.

Мерой инертности тела в прямолинейном движении выступает его масса. Больше масса – больше инертность тела.

Инерция, кинетическая энергия, работа

Приведем другой пример. Представь тяжелоатлета… Даже двух, которые решили поставить мировой рекорд и сдвинуть самолет. Им придется приложить немало сил, чтобы вначале разогнать самолет от нуля до некоторой скорости, а потом поддерживать эту скорость, преодолевая силу трения, направленную назад. Конечно, проще сдвинуть с места (преодолеть инерцию покоя) и разогнать до большой скорости тело меньшей массы, например, футбольный мяч. Инертность самолета во много раз больше инертности футбольного мяча.

А к какому трюку прибегает фокусник, чтобы в случае со скатертью все предметы остались на столе? Правильно, нужно выдернуть скатерть за наименьшее время. Чем меньше время, тем меньше энергии перейдет с силой трения на предметы и они просто не успеют разогнаться.

Энергия движущегося тела называется кинетической энергией и измеряется в Джоулях. Если тело неподвижно, кинетическая энергия равна нулю.

Чтобы разогнать тело массой m до нужной скорости V из состояния покоя (например, самолет), нужно выполнить работу, равную кинетической энергии разогнанного тела (без учета разных потерь):

Работа по изменению кинетической энергии тела совершается за счет приложения к нему некоторой силы – силы тяжести, силы трения, силы воздействия на него другого тела (тяжелоатлета-силача, дующего ветра, реактивной тяги ракетного двигателя и пр.).

Пусть силач разогнал до 0.1 м/с (10 сантиметров в секунду) легковую машину массой 1200 кг и самолет Ил-76 массой 88 500 кг в космосе (не будем учитывать силу трения). Тогда для преодоления инерции этих тел ему пришлось сжечь мышечной энергии на 6 Дж и 442,5 Дж соответсвенно. Т.е. на преодоление инерции покоя у самолета у спортсмена уйдет в 74 раза больше энергии, чем на автомобиль.

Чтобы остановить тело массой m, движущееся со скоростью V, нужно совершить обратную работу, равную отрицательному значению кинетической энергии этого тела:

Т.е. чем больше скорость тела и его масса, тем больше энергии на преодоление инерции движения надо затратить.

Если выключить мотор, машина под действием силы трения ее движущихся частей друг о друга, силы трения о воздух корпуса и силы трения колес об асфальт остановится сама. Но остановить машину можно и быстрее, увеличив силу трения с помощью тормозных дисков, т.е. выжав педаль тормоза.

При равной скорости масса грузовика намного больше, а значит больше его кинетическая энергия. Двигаясь накатом грузовик остановится дальше, чем легковой автомобиль – его инертность выше. Кстати, можно ли остановить грузовик быстрее легкового автомобиля и при каких условиях?

Момент инерции

Инерция проявляется не только для прямолинейного движения, но и при вращении тел. В двигателе есть специальное устройство – маховик (на рисунке справа маховик покрашен темно-серым цветом и имеет зубчики). Инерция его вращения помогает работать двигателю нормально. Энергия расширяющихся газов при воспламенении топлива толкает поршень вниз, а затем ему нужно идти вверх, выталкивая продукты сгорания. Без маховика поршень не смог бы провернуть коленвал без рывков. Двигатель без маховика заглохнет.

Ну а со спинерами и волчками знакомы многие.

Вот только в приведенных примерах форма тела не меняется. А изменится ли инертность тела при изменении его формы?

Вращение на фигурном катании

Многие могут вспомнить фигурное катание. Масса тела фигуриста за выступление не меняется. Но его скорость вращения мгновенно увеличивается, стоит прижать руки и ноги, и вытянуться в струнку. Т.е. при уменьшении радиуса тела скорость вращения увеличивается. Т.е. инертность тела должна уменьшиться? Давайте разбираться.

Вернемся к формулам. Скорость вращающегося тела описывается как произведение угловой скорости (омега) на радиус:

Скорость вращающегося тела

При этом кинетическая энергия вращающегося тела примет вид:

Синим цветом выделено произведение массы тела на радиус в квадрате. Эта величина называется моментом инерции вращающегося тела и обозначается латинской буквой I (и).

Мерой инертности вращающего тела выступает момент инерции, который зависит от массы тела и расстояния этой массы от центра вращения.

Представим, что девочка не только вращает груз над собой, но и идет. Тогда полная кинетическая энергия девочки с грузом примет вид:

Первая часть описывает кинетическую энергию двигающейся прямолинейно с некоторой скоростью девочки с грузом, а вторая – кинетическую энергию вращающегося груза. Полная кинетическая энергия — это сумма энергии прямолинейно движущегося тела и энергии вращающегося тела. Точно так же кинетическая энергия будет рассчитываться для движущегося по столу раскрученного волчка или съезжающего с наклонной плоскости цилиндра.

Так как вращающееся тело может иметь форму, отличную от точки или маленького шарика, то и формула момента инерции для более точных расчетов может принимать разный вид.

Пример.

Цилиндры одинаковой массы (m1 = m2), но разного радиуса (r₁ Цилиндры одинаковой массы, но разного радиуса, скатываются с горки высотой h

В верхней точке кинетическая энергия обоих цилиндров будет равна нулю, так как скорость равна нулю. Потенциальная энергия будет одинаковой и максимальной.

При скатывании цилиндров по закону сохранения энергии потенциальная энергия переходит в кинетическую и в самой нижней точке будет равна нулю, так как высота равна нулю. А кинетическая энергия в нижней точке будет складываться из поступательной кинетической энергии и кинетической энергии вращающегося тела и у обоих тел также будет одинаковой, так как их потенциальные энергии были равны.

Но так как радиус первого тела меньше второго, то и момент инерции первого тела меньше второго и будет справедливо:

Тогда для кинетической энергии поступательного движения будет справедливо отношение:

Следовательно, скорость первого цилиндра должна быть выше скорости второго, и он скатится быстрее. Так как мерой инертности вращающегося тела является момент инерции, то первое тело с меньшим радиусом и меньшим моментом инерции будет обладать меньшей инертностью, чем второе. Разогнаться под действием каких-либо сил (силы тяжести) такому телу проще.

Вопросы

1. Посмотри на картинку с формулами для расчета момента инерции для тел разной формы. Как ты думаешь, какая формула лучше подходит для расчёта момента инерции маховика автомобиля. Варианты ответа: a, b, c, d, e, f, g, h, или i

Маховик автомобиля

2. Два волчка одинаковой массы раскрутили до одинаковой угловой скорости, но диаметр первого волчка меньше диаметра второго. Какой из них упадет раньше?

3. На рисунке показаны три варианта конструкции. Какой вариант машинки имеет наименьшую инертность, а какой максимальную? Почему?

Источник