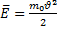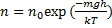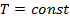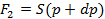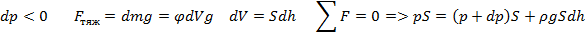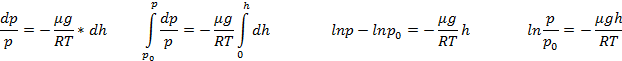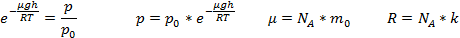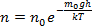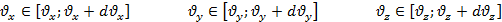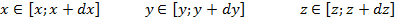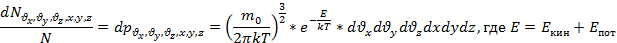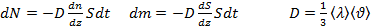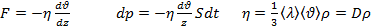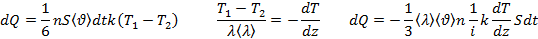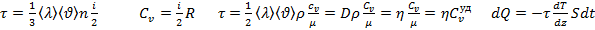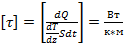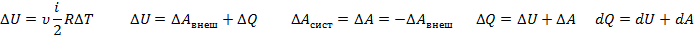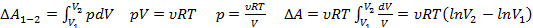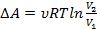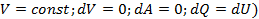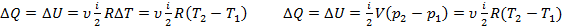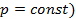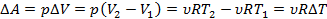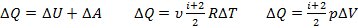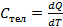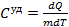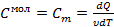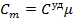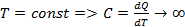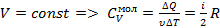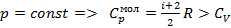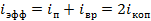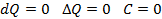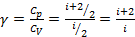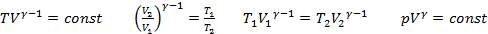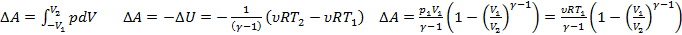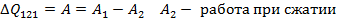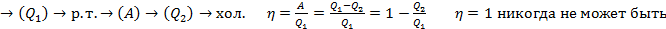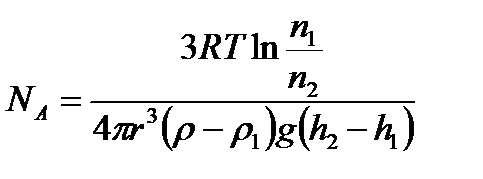молекулы газа находящиеся в поле тяготения

Идеальный газ в поле силы тяжести. Барометрическая формула.Распределение Больцмана.

Макроскопическая система, макроскопические параметры. Идеальный газ, уравнение состояния идеального газа.

Макроскопические параметры – параметры значения, которых можно определить с помощью приборов, ничего не зная об атомно-молекулярном строении вещества (давление, объем, температура).

Идеальным называют газ, взаимодействием, между молекулами которого можно пренебречь.

Уравнения состояния идеального газа:

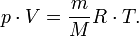
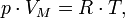
Законы идеальных газов: Бойля-Мариотта, Гей-Люссака, Авогадро, Дальтона.

Закон Бойля-Мариотта: При постоянной температуре и массе идеального газа произведение его давления и объёма постоянно. Формула: pV = const

Закон Гей-Люссака:при постоянном давлении объём постоянной массы газа пропорционален абсолютной температуре. Формула: V/T=const

Закон Авогадро: в равных объёмах различных газов, взятых при одинаковых температуре и давлении, содержится одно и то же число молекул.

Закон Дальтона: Давление смеси химически не взаимодействующих идеальных газов равно сумме парциальных давлений.

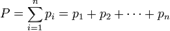
Внутренняя энергия идеального газа. Степени свободы. Теорема о равномерном распределении кинетической энергии по степеням свободы.

В теории идеального газа потенциальная энергия взаимодействия молекул считается равной нулю. Поэтому внутренняя энергия идеального газа определяется кинетической энергией движения всех его молекул. Формула:

Степени свободы — характеристики движения механической системы. Число степеней свободы определяет минимальное количество независимых переменных, необходимых для полного описания движения механической системы.

В состоянии термодинамического равновесия на каждую степень свободы движения частиц вещества приходится кинетическая энергия в среднем, равная kT/2.

Основное уравнение молекулярно-кинетической теории. Средняя кинетическая энергия молекул, молекулярно-кинетический смысл температуры.

Основное уравнение МКТ связывает макроскопические параметрыгазовой системы с микроскопическими.

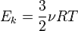
Средняя кинетическая энергия молекул:

Температура определяется через микроскопические характеристики системы и служит мерой энергии неупорядоченного движения частиц.

5. Функция распределения молекул по скоростям. Распределение Максвелла.

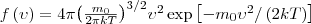
Идеальный газ в поле силы тяжести. Барометрическая формула.Распределение Больцмана.

В идеальном газе, находящемся во внешнем поле сил, каждая отдельная частица приобретает импульс в направлении силы, а также соответствующую потенциальную энергию. Однако в газе наряду с упорядоченным движением в направлении действия силы существует хаотическое тепловое движение. В результате конкуренции между этими двумя типами движений возникает неравномерное распределение макроскопических параметров: плотности частиц, давления, температуры по объему, занимаемому газом.

Барометрическая формула — зависимость давления или плотности газа от высоты в поле тяжести.

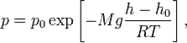
В присутствии гравитационного поля (или, в общем случае, любого потенциального поля) на молекулы газа действует сила тяжести. В результате, концентрация молекул газа оказывается зависящей от высоты в соответствии с законом распределения Больцмана:

Источник

2.1.4. Идеальный газ в поле силы тяжести

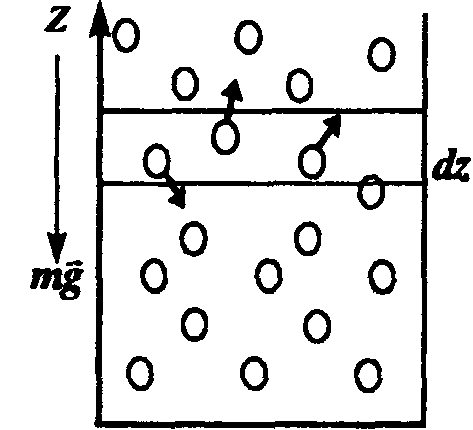
Каково поведение идеального газа в поле внешней силы? Для определенности в качестве внешней силы возьмем хорошо известную силу тяжести mg. Под действием внешней силы механическая система частиц приобретает импульс и перемещается как целое поступательно в направлении силы. В идеальном газе, находящемся во внешнем поле сил, каждая отдельная частица приобретает импульс в направлении силы, а также соответствующую потенциальную энергию. Однако в газе наряду с упорядоченным движением в направлении действия силы существует хаотическое тепловое движение. В результате конкуренции между этими двумя типами движений возникает неравномерное распределение макроскопических параметров: плотности частиц, давления, температуры по объему, занимаемому газом.

Рассмотрим столб газа сечением S, находящийся при постоянной температуре в поле силы тяжести. Выделим слой газа толщинойdz на высотеzи вычислим давление газа на его основания. Давление слоя газа на верхнее и нижнее основания слоя разное — оно различается в результате действия силы тяжести. Очевидно, разность давлений равна весу газа, заключенного в слое, отнесенному к единице площади основания столба.

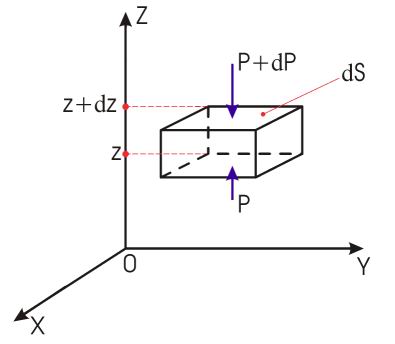
Пусть разность давлений есть dP. Давление газа с ростом высоты уменьшается, поэтомуdP равно весу слоя со знаком минус. Вес газа в объеме слояdV =dz·S равен ρ·g·dV, где ρ — плотность газа,g — ускорение силы тяжести. Таким образом,

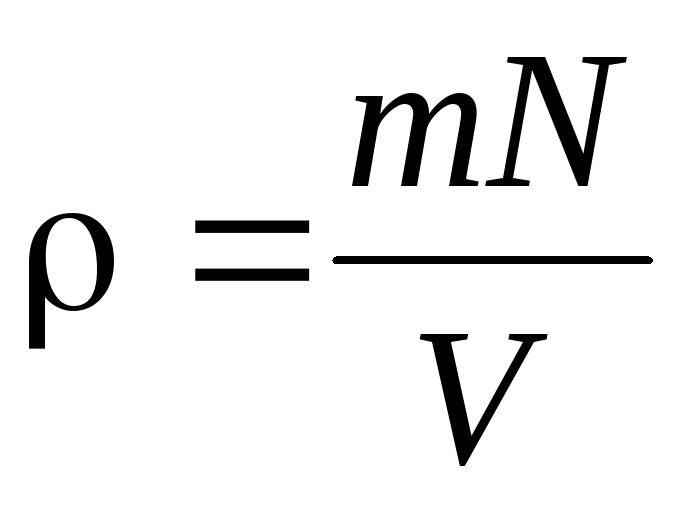
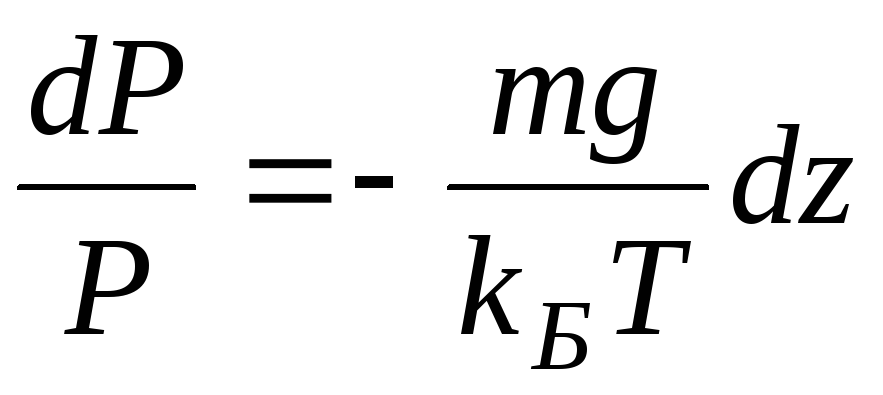
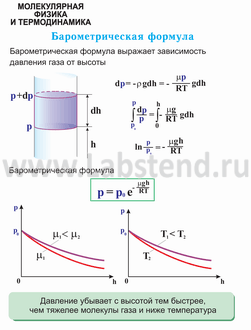
По определению . Выразим отношениеN/V с помощью уравнения состояния (2.7), после чего находим:

.

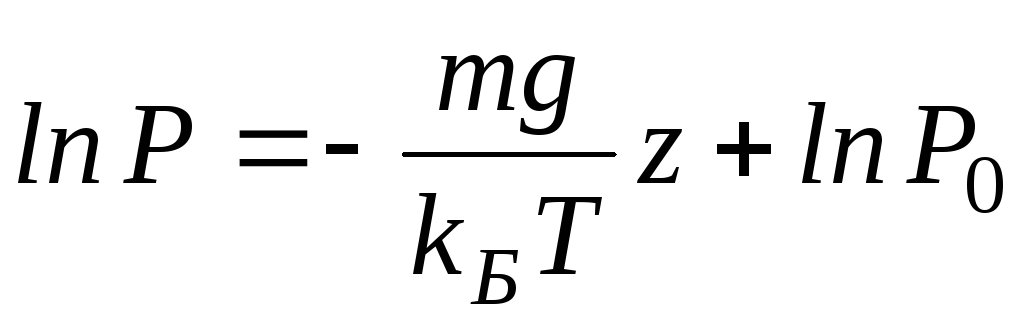
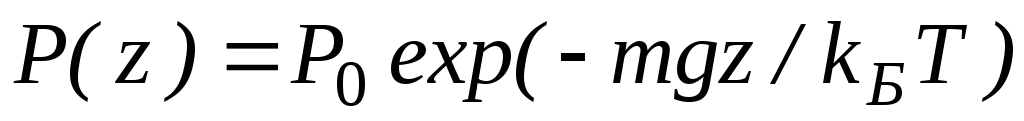
Интегрируя это соотношение, получим , гдеP₀ — константа, определяемая пределами интегрирования. Окончательно имеем:

. (2.9)

Здесь P₀ — давление приz = 0. т. е. у основания столба. Аналогично с высотой изменяется и плотность частиц

. (2.10)

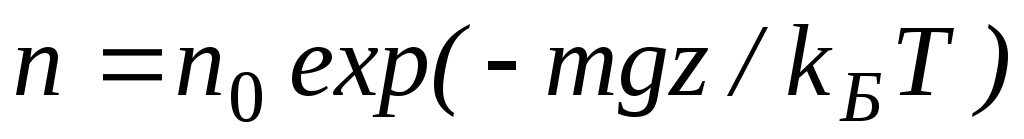
Давление и плотность газа распределены по объему газа неоднородно, они принимают максимальные значения у основания столба и убывают с высотой.

Величина, входящая в показатель экспоненты в формулах (2.9) и (2.10), есть потенциальная энергия частицы в поле тяжести U =mgz-Таким образом, распределение молекул в произвольном потенциальном внешнем поле, в котором частицы обладают потенциальной энергиейU(r), может быть описано формулой:

. (2.11).

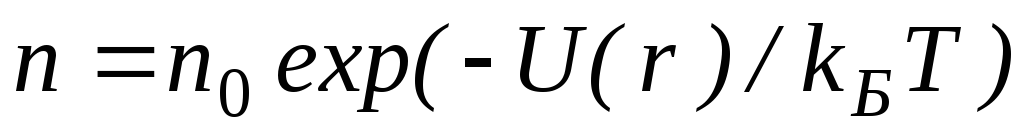
Эта формула называется распределением Больцмана. Здесь n₀ — плотность частиц в точках пространства, для которых потенциальная энергия принята равной нулю.

Согласно распределению Больцмана число частиц, обладающих определенными значениями потенциальной энергии определяется отношением величины потенциальной энергии U к тепловой энергии частицыk_БT. Чем больше энергия теплового движения, тем более разупорядочена система частиц, значит, тем более однородно распределены частицы в пространстве. В самом деле, еслиk_БT >>U,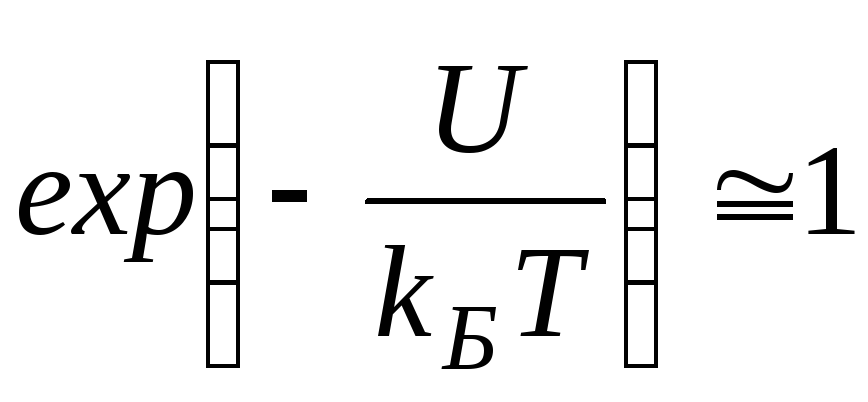, и из формулы (2.11) следует, чтоn =n₀ при любом значенииU. В случаеk_БT 17 / 34 17 18 19 20 21 22 23 24 25 > Следующая > >>

Тут вы можете оставить комментарий к выбранному абзацу или сообщить об ошибке.

Источник

Газ в поле тяготения. Барометрическая формула. Распределение Больцмана.

1)поле однородно

3)

Равновестное распределение молекул устанавливается в результате одновременного действия двух конкурирующих факторов:

1.Газ стремится занять весь предоставленый ему объем.

2.Молекулы притягиваются к земле.

показывает во сколько раз отличаются концентрации частиц в 2 точках, если их потенциальные энергии в этих точках отличаются (распределение частиц по координатам).

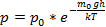
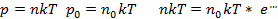
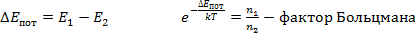
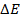
25. Столкновения молекул. Средняя длина свободного пробега. Эффективный диаметр молекул.

Минимальное расстояние, на которое сближаются при столкновении центры двух молекул, называется эффективным диаметром молекулыd. Он за­висит от скорости сталкивающихся моле­кул, т. е. от температуры газа (несколько уменьшается с ростом температуры).

Эффективный диаметр молекулы- это min расстояние до которого могут свдвинутся две молекулы.

Эффективное сечение – это сечение шара, который описан вокруг молекулы.

Вакуум- это такое состояние газа, когда длина свободного пробега соизмеряется длиной сосуда.

26. Диффузия, внутреннее трение, теплопроводность. Коэффициенты диффузии, вязкости и теплопроводности.

Диффузия:

Внутреннее трение в твёрдых телах, свойство твёрдых тел необратимо превращать теплоту в механическую энергию, сообщенную телу в процессе его деформирования. В. т. связано с двумя различными группами явлений — неупругостью и пластической деформацией.

Вязкость:

Теплопроводность:

— коэффициент теплопроводности

— коэф. теплопроводности численно равен кол-ву теплоты перенесенной за единицу времени через единичную площадку при единичном градиенте температур.

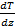
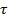
27. Термодинамика. Первое начало термодинамики. Теплоемкости газа. Работа и теплоемкость при изопроцессах. Зависимость теплоемкости от температуры.

Термодинамика- наука о наиболее общих св-вах макросистем о находящихся в состоянии термодинамического равновесия и о процессах перехода между этими состояниями.

Вн. энергия- суммарная энергия

Теплота, сообщенная системе идет на работу системы против внешних сил и на приращение внутренней энергии системы.

2)изохора (

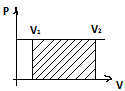
3)изобара (

Газовая постоянная численна равна работе одного моля идеального газа, при изобарном нагреве на 1К.

1)Теплоемкость- кол-во теплоты, которое нужно собщить всему телу на повышение температуры на 1К.

2)Теплоемкость удельная- кол-во теплоты, которое нужно сообщить единице массы на повышение температуры на 1К.

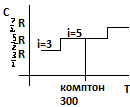
3)Теплоемкость молярная- кол-во теплоты, которое нужно сообщить 1 молю в-ва чтобы нагреть его на 1 К.

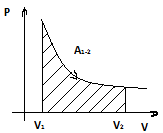
1)

2)

3)

28. Адиабатический процесс. Работа при адиабатическом процессе. Уравнение Пуассона.

Адиабата- процесс без теплообмена с окр. средой.

Показатель Пуассона

Уравнение Пуассона

29. Круговой процесс (цикл). КПД цикла. Обратимые и необратимые процессы. Второе начало термодинамики по Кельвину и Клаузиусу

Цикл – это процесс, в котором система, пройдя ряд последовательных состояний возвращается в исходное.

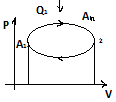
Наг.

Обратимые и не обратимые процессы.

Процесс называется обратимым, если он может идти как в прямом, так и в обратном направлении, при этом, если система возвращается в исх. состоянии, то ни в самой системе, ни в окр.среде не происходит никаких изменений. Все равновесные процессы обратимы. Равновесный процесс – это процесс, любая точка которого это состояние равновесия. Только равновесные процессы изображают на графиках.

Все реальные процессы необратимы. Необратимые: теплопроводность, диффузия, вязкость, трение.

КПД выше если процесс наиболее близок к идеальному.

Второе начало термодинамики.

Карно доказал, что невозможно построить вечный двигатель второго рода( 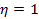), т.е. невозможен процесс единственным результатом которого будет превращение всей теплоты полученной от нагревателя в эквивалентную ей работу.

По Клаузиусу: невозможно без совершения дополнительной работы передавать теплоту от холодного к горячему.

Дата добавления: 2018-02-18 ; просмотров: 666 ; Мы поможем в написании вашей работы!

Источник

Идеальный газ во внешнем гравитационном поле

Пусть ИГ находится во внешнем гравитационном поле (в поле силы тяжести Земли). При нахождении концентрации молекул газа n(x, y, z) в этом поле будем исходить из предположения, что любой бесконечно малый объем газа находится в состоянии механического равновесия, а температура газа T во всех точках одинакова. Только при выполнении этих условий состояние газа можно считать равновесным, так как иначе в газе возникли бы потоки вещества и теплоты, что сделало бы состояние газа неравновесным.

Поле силы тяжести Земли будем считать однородным. Ось OZ направлена вертикально вверх. Тогда концентрация молекул газа будет зависеть только от координаты z (высоты h): n=n(z)или n=n(h). На рис. (1) схематически изображен бесконечно малый выделенный объем газа dV=dSdz, находящийся в равновесии.

Снизу на этот выделенный объем газа воздействует давление p, а сверху – соответственно давление p+dp. Разность давлений на нижнее и верхнее основание выделенного объема газа dV=dSdz равна гидростатическому давлению:

где: r=(Mp)/(RT) – плотность газа, g – ускорение свободного падения, M – молярная масса газа.

Подставим в полученное выражения плотность газа:

Из этого уравнения следует, что

Интегрирование последнего уравнения при условии позволяет определить зависимость давления от высоты:

где p₀ — давление газа на высоте, принятой за начало отсчета.

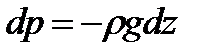
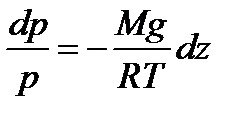
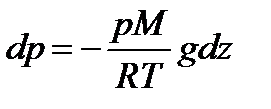
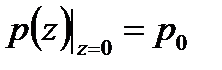
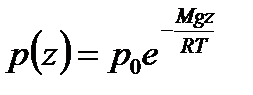
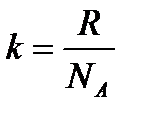
С учетом формулы для постоянной Больцмана:

Барометрическая формула:

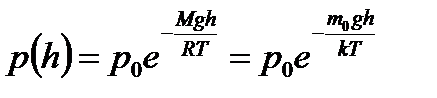
270 К на высоте около 55 км. На этой высоте давление атмосферы становится уже меньше 0,001 от атмосферного давления на уровне моря.

Несмотря на указанную зависимость температуры атмосферы Земли от высоты, барометрическая формула позволяет достаточно точно определять высоту по результатам измерения давления, что нашло применение в приборах, предназначенных для определения высоты полета самолетов.

Распределение Больцмана было получено в 1866 году Л. Больцманом. Это распределение позволяет рассчитывать концентрацию газа, находящегося в равновесном состоянии во внешнем силовом поле. Причем это поле не должно быть обязательно гравитационным, а может иметь любое происхождение, в частности, быть электростатическим или полем сил инерции.

Анализ распределения Больцмана показывает, что концентрация молекул газа тем выше, чем меньше их потенциальная энергия. Кроме этого, с понижением температуры увеличивается отличие концентраций в точках с различными значениями потенциальной энергии молекул. А при стремлении температуры к абсолютному нулю, молекулы начинают скапливаться в месте, где их потенциальная энергия принимает наименьшее значение. Указанные особенности распределения Больцмана являются следствием теплового движения молекул, так как кинетическая энергия их поступательного движения в среднем равна W_к=(3/2)kT и уменьшается пропорционально уменьшению температуры. А уменьшение кинетической энергии приводит к уменьшению количества молекул, способных преодолеть потенциальный порог, высота которого характеризуется величиной потенциальной энергии высотой W_p.

Опыт Перрена.

Распределение Больцмана было использовано французским физиком Жаном Батистом Перреном (1870–1942) при экспериментальном определения постоянной Больцмана k и постоянной Авогадро N_A.

В работах, выполненных Перреном в 1908-1911 гг., измерялось распределение концентрации микроскопических частиц во внешнем гравитационном поле. Отметим, что совокупность микрочастиц, находящихся во взвешенном состоянии в жидкости, близка по своей молекулярно-кинетической структуре к идеальному газу и может описываться газовыми законами. Это дает возможность при определении распределения микрочастиц во внешнем силовом поле использовать формулу Больцмана.

Исследуя в микроскоп броуновское движение, Ж. Перрен убедился, что броуновские частицы распределяются по высоте подобно молекулам газа в поле тяготения. Применив к этим частицам больцмановское распределение, можно записать:

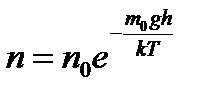
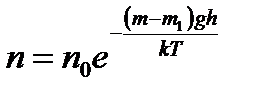
где m – масса частицы,

m₁– масса вытесненной ею жидкости;

m=4/3πr 3 ρ, m₁= 4/3πr 3 ρ₁

(r – радиус частицы, ρ – плотность частицы, ρ₁– плотность жидкости).

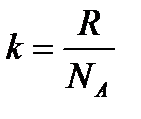
Значение N_A, получаемое из работ Ж. Перрена, соответствовало значениям, полученным в других опытах. Это подтверждает применимость к броуновским частицам распределения Больцмана.

Источник