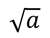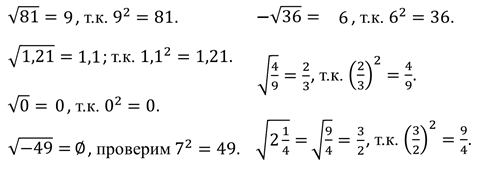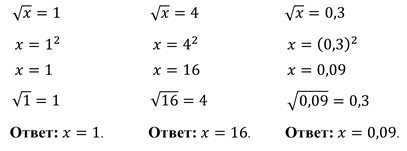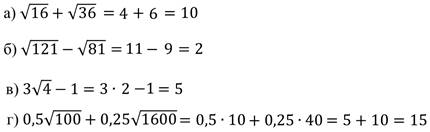квадратный корень какой класс
Алгебра. 8 класс
Квадратным корнем из числа b называют такое число, квадрат которого равен b.
Арифметическим квадратным корнем из числа b называют неотрицательное число, квадрат которого равен b.
Обозначение арифметического квадратного корня: 
.
– знак корня, или знак радикала.
Выражение под знаком корня называют подкоренным выражением.
b – подкоренное выражение.
, если:
1) а ≥ 0,
2) a 2 = b.
, так как
1) 9 ≥ 0,
2) 9 2 = 81.
, так как
1) 0 ≥ 0,
2) 0 2 = 0.
Из определения арифметического квадратного корня следует равенство 
.
Алгебра. 8 класс: учеб. для общеобразоват. организаций / [Ю. Н. Макарычев, Н. Г. Миндюк, К. И. Нешков, С. Б. Суворова]; под ред. С. А. Теляковского. – 6-е изд. – М.: Просвещение, 2017.
Технологическая карта урока математики 8 класс «Арифметический квадратный корень»
Ищем педагогов в команду «Инфоурок»
Учитель математики МКОУ Дресвянской ООШ
Урок «Квадратный корень. Арифметический квадратный корень».
Тема урока: Квадратный корень. Арифметический квадратный корень. Свойства квадратного корня.
Тип урока: Урок изучения нового материала
Обучающа я: формирование понятия: квадратный корень, арифметический квадратный корень; изучение свойств арифметического квадратного корня; отработка умений и навыков вычисления значения корня.
Воспитательная: воспитание коммуникабельности и положительного отношения к учебной деятельности.
Развивающая: развитие логического мышления, самостоятельности; совершенствование умений применять накопленные знания в изменённой ситуации.
Оборудование: компьютеры, мультимедийный проектор, экран.
Предметные:
Оперировать понятиями, связанными с квадратными корнями. работать с математическим текстом, выражать свои мысли в устной и письменной речи, применяя математическую терминологию и символику; использовать словесный, символический, графический языки математики для доказательства математических утверждений;
Определять границы собственного знания и незнания. желание приобретать новые знания и совершенствовать имеющиеся. Формировать готовность и способность обучающихся к самореализации и самообразованию на основе развития мотивации(через проблему, интерес, ситуацию успеха- придумать пример) учебной деятельности; в коммуникационной сфере понимать и уважать позицию собеседника, достигать взаимопонимания, сотрудничать для достижения общих результатов; ясно, точно, грамотно излагать свои мысли в устной и письменной речи, понимать смысл поставленной задачи,
Познавательные: у мение ориентироваться в своей системе знаний: отличать новое от уже известного; умения находить необходимую информацию в источниках (в учебнике) представлять информацию в различной форме (словесной, графической, символической), обрабатывать, передавать информацию
Коммуникативные: умение слушать и вступать в диалог, участвовать в коллективном обсуждении проблем, высказывать и аргументировать свою точку зрения, умение отвечать на вопросы, обсуждать вопросы со сверстниками;
Регулятивные: умение организовать выполнение заданий согласно инструкциям учителя, формулировать постановку учебной задачи, оценивать уровень владения учебным материалом, осуществлять коррекцию знаний.
Формирование УУД, технология оценивания
Цели: проверка готовности обучающихся, включить обучающихся в учебную деятельность, определить содержательные рамки урока
Организует учащихся: приветствует учащихся, проверяет готовность обучающихся к уроку, создаёт благоприятный психологический настрой на работу.
Прием «Корзина идей»
Проверяют наличие необходимых учебных принадлежностей. Концентрация внимания, воли,
Включаются в деловой ритм урока.
Предлагают ответы на вопрос: какое отношение рисунок имеет к уроку?
(К) планирование учебного сотрудничества с учителем и сверстниками.
(Р) организация своей учебной деятельности.
(Л) мотивация учения
II . Актуализация опорных знаний.
Цель: актуализация опорных знаний
Мотивация учебной деятельности учащихся
Включает учащихся в деятельность.
Учащимся предлагается для решения следующая задача, при этом они не знакомы с уравнением вида х 2 =а. Учащиеся, применяя метод подбора, выходят на решение задачи.
Для строительства забора необходимо найти периметр данного участка квадратной формы. Известно, что площадь участка 625 см2 .
Учащиеся в коммуникативной форме формулируют конкретную цель своих будущих учебных действий, устраняющих причину возникшего затруднения (то есть формулируют, какие знания им нужно построить и чему научиться);
· умение выражать свои мысли;
· отстаивать свою точку зрения;
III .Подготовка к изучению нового материала (стадия вызова).
Организует работу обучающихся.
Правильность решения задачи проверяется по слайду презентации.
Таким образом, мы решили уравнение х 2 =625, которое имеет два корня х=-25 и х=25.
Так как 25 2 =625 и (-25) 2 =625
· умения слушать ответы товарища и отвечать на вопросы других;
· формулировать собственные мысли;
· высказывать и обосновывать свою точку зрения;
· управлять поведением партнера.
· выделять ключевые моменты.
· положительно относиться к учению, к познавательной деятельности;
· желание приобретать новые знания и совершенствовать имеющиеся.
Постановка цели и задач урока
1. Мотивирует учащихся, вместе с ними определяет тему и задачи урока; ход урока
Формулируют тему урока. Определяют цели.
П. Самостоятельное формулирование темы и задач урока. Умеют осознано и произвольно строить умозаключение
Р. Выбор и принятие целей
IV .Усвоение нового материала (стадия осмысления).
1.Направляет работу обучающихся.
Что же называется квадратным корнем?
2. Координирует, направляет работу обучающихся, помогает найти нужную информацию.
4. Помогает обобщить материал
Более слабые ученики, работая с учебником, дают определение арифметического квадратного корня.
· читать и извлекать нужную информацию;
· умение работать с текстом;
· анализировать, сравнивать новые знания с полученными ранее;
· формулировать собственные мысли.
V. Первичное закрепление
Цель: первичное закрепление нового способа действий с проговариванием.
Комментирует, направляет работу учащихся.
Организует парную работу(найти ошибки в вычислениях) и его проверку .
Выполняют задание письменно. Комментируют решения примеров.
Парная работа : выполняют задания, осуществляют проверку
Используя определение арифметического квадратного корня, найдите значения выражений
В ходе наблюдения учащиеся самостоятельно приходят к выводу, что выражения 
не имеют смысла.
П) формирование интереса к данной теме.
(Л): формирование позитивной самооценки, учатся принимать причины успеха (неуспеха).
(Р): планирование своей деятельности для решения поставленной задачи оценка и коррекция полученного результатадля повышения мотивации учебной деятельности.
(К): Строят рассуждения, используют речь для регуляции своего действия, вступают в диалог, уважительно относится к мнению другого.
VII. Самостоятельная работа.
Цель: закрепление нового способа действий
Организует и контролирует процесс решения.
Выступает в роли тьютора для слабых учащихся
1. В классе работают две группы. Первая отрабатывает навыки нахождения значения квадратного корня на ПК. После выполнения задания «Тренажёр» выставляется оценка в журнал. Учащиеся имеют возможность проанализировать допущенные ошибки и исправить их, пройдя повторно неверно выполненные задания.
Вторая группа работает вместе с учителем по учебнику.
Разбирается материал вторично, уточняются отдельные моменты, еще раз аргументируются основные положения и выполняются упражнения на доске с комментарием.( №288, 289 (б,г,е,з,л)
3. Затем ученикам с высокими учебными возможностями предлагается поработать самостоятельно по номерам №290,293,300.
Вторая группа в это время работает на ПК с программой «Тренажёр».
(Л): формирование готовности к самообразованию.
(К): уметь оформлять свои мысли в устной форме, задавать вопросы, необходимые для организации собственной деятельности и сотрудничества с учителем
Цель: Подведение итогов работы
. Что нового мы узнали? В чем испытали затруднение?
За что себя можешь похвалить.
Оцените свою работу.
Подводят итоги своей работы
· Какую задачу ставили? (см.кластер)
· Каким способом решали поставленную задачу?
Оценивают себя через корень.
Выясяют :Растут ли радикалы на грядке?
(Р): оценивание собственной деятельности на уроке.
(К): уметь слушать и вступать в диалог.
.Информация о домашнем задании
Организовывает обсуждение домашнего задания
Квадратные корни. Арифметический квадратный корень
Урок 11. Алгебра 8 класс ФГОС
В данный момент вы не можете посмотреть или раздать видеоурок ученикам
Чтобы получить доступ к этому и другим видеоурокам комплекта, вам нужно добавить его в личный кабинет, приобрев в каталоге.
Получите невероятные возможности
Конспект урока «Квадратные корни. Арифметический квадратный корень»
На этом уроке мы познакомимся с новыми для вас понятиями такими, как квадратные корни и арифметический квадратный корень. А также научимся находить значения корней.
Числа 10 и минус 10 называют квадратными корнями уравнения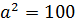 
.
Квадратным корнем из числа а называют число, квадрат которого равен а.
Вернёмся к задаче. Мы знаем, что длина – это положительная величина. А значит, корень второго уравнения – минус 10, не подходит. И тогда длина стороны Машиной клумбы равна 10 метрам.
Решая данную задачу, мы с вами столкнулись с неоднозначностью: получили два корня, но к решению задачи подошел только один. И чтобы не было проблем с выбором корня вводят понятие арифметического квадратного корня.
Арифметическим квадратным корнем из числа а называется неотрицательное число, квадрат которого равен а.
Обратите внимание, в определении прозвучала фраза «неотрицательное число». Почему нельзя сказать просто … «положительное число»? … Потому что квадрат нуля, есть само число нуль. А оно, как вы знаете, не является ни положительным числом, ни отрицательным. Поэтому и используют термин «неотрицательное число».
Арифметический квадратный корень из числа а обозначают так:
Знак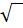 
называют знаком арифметического квадратного корня или знаком радикала (от латинского слова «радикс» – корень).
Выражение, стоящее под знаком корня называют подкоренным выражением.
При чтении записи, слово «арифметический» не произносят, а читают просто «квадратный корень из а».
Операцию нахождения арифметического квадратного корня из числа, называют извлечением корня.
Рассмотрим несколько примеров извлечения корня из числа. Итак, найдём значения корней.
Запомните, квадратный корень можно извлекать только из неотрицательных чисел.
При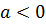 
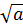
выражение 
не имеет смысла. Т.к. нет такого числа квадрат, которого бы был отрицательным числом.
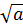
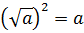
Из определения арифметического квадратного корня следует, что при любом а, при котором выражение имеет смысл, верно равенство 
.
Задание 1: найдите число, арифметический квадратный корень из которого равен: 1; 4; 0,3.
Задание 2: найдите значение выражения.
Квадратным корнем из числа а называют число, квадрат которого равен а.
Арифметическим квадратным корнем из числа а называется неотрицательное число, квадрат которого равен а.
Операцию нахождения арифметического квадратного корня из числа, называют извлечением корня.
Равенство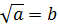 
верно, когда выполняются два условия:
1) 
и 2) 
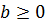
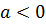
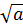
При выражение не имеет смысла.
Из определения арифметического квадратного корня следует, что при любом а, при котором выражение 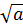имеет смысл, верно равенство
В каком классе изучают квадратный корень?
Лично я начал изучать квадратный корень в 8 классе.
Во первых есть какие-то определенные обычаи в школах,как переход из начальных классов в старшие классы.Поэтому принято делать выпускной в четвертом классе.Но это вопрос родителей.Если родители считают нужным,они организуют выпускной для своих детей и учителей,а если не считают,то можно и без выпускного обойтись.
Известны случаи,когда одни родители старались сделать выпускной дороже,устраивали его в кафе и даже в ресторанах и было скучно,а другие в школе с участием тамады и сладкого стола и было весело и не дорого.
Скорей всего, Вы имеете в виду не исторические, а политические взгляды Л.Н. Толстого. В рассказе «После бала» автор резко противопоставляет добродушие полковника на балу, где он выступает в роли отца, и его жестокость в сцене с солдатом, где отец возлюбленной героя становится олицетворением системы. Стоит напомнить, где действия рассказа происходит во времена царствования императора Николая I, известного своей жестокостью.
Последний звонок обычно бывает в последних числах мая.
В походы, наверное, ходят, но намного реже, не так как раньше. И скорее всего ходят те, кто живёт и учиться не в столице и больших городах, кто живёт в маленьком городе, где относительно близко лес и горы. И ещё очень многое в этом вопросе зависит от классного руководителя и активности хотя бы некоторых родителей, которым не безразлично, то как растёт,учится, развивается и отдыхает их ребенок.
Урок алгебры в 8-м классе по теме «Квадратный корень из произведения и дроби»
Разделы: Математика
Ход урока
I. Организационный момент
Сегодня у нас не совсем обычный урок, к нам пришли гости. Посмотрите на наших гостей, улыбнитесь им, посмотрите друг на друга и тоже улыбнитесь, ведь от улыбки станет всем теплей, поднимется настроение. Ребята, я вас попрошу поставить на полях своих тетрадей ту оценку, которую вы хотели бы получить за урок.
Предлагаю вам выполнить письменную работу “Математический словарь”
Взаимопроверка. Как вы считаете, какая тема объединяет эти математические термины?
( Квадратные корни.) А какую тему мы изучали на прошлом уроке? (Квадратный корень из произведения и дроби.)
Постановка целей урока.
Для того чтобы урок прошел успешно, необходимо повторить теорию.
II. Устная работа
Учитель задает учащимся те вопросы, которые не прозвучали в ходе опроса.
а) 
;
б) 
;
в) 
;
г) 
;
д) 
;
е) 
Даются подробные объяснения.
3. Сравните: 
и 
.
III. Работа на доске и в тетрадях со всеми учащимися
1. Учитель: А как вы нашли произведение и частное корней?
Ученик: Поменяв в тождествах 
=
и 
= 
местами их левые и правые части, получим:
| = и = |
Вопрос. В каком случае пользуются этими тождествами? (При умножении и делении квадратных корней).
2. Разобрать решение примеров 4 и 5 на с. 86 учебника.
3. Решить № 385 (а, б, в, ж) на доске и в тетрадях.
4. Решить № 386 самостоятельно с проверкой. Один ученик решает самостоятельно у доски, остальные учащиеся решают в тетрадях. Если возникают затруднения, можно обратиться за помощью к соседу по парте или к учителю. Затем проверяется решение.
IV. Задания по выбору.
1. Используя свойства квадратного корня, найдите с помощью таблицы квадратов, значение выражения:
; 
; 
; 
; 
; 
; 
; 
.
Самопроверка с помощью микрокалькулятора.
Ответы: 15; 18; 22; 270; 1,1; 4,1; 0,36; 70.
1) Вычислите 
.
1) 3 
2) 1,4
3) 1 
4) 1,5
2) Решите уравнение 0,5у 2 = 8.
4)Применив свойства арифметического квадратного корня, вычислите 
.
5) Вычислите 
без помощи микрокалькулятора.
6) Даны числа: 0, (7); 1
; 
; 
. Сколько среди них рациональных?
Самопроверка. Работа над ошибками. Итог.
V. Творческое задание “Смотри, не ошибись!”
Определить неизвестный множитель:
? = а;
( + 
) (?) = а – в;
? = в;
( 
— 1) (?) = 1.
VI. Задание “Проверь, не пользуясь микрокалькулятором ”
= 
= 60.
VII. Резервное задание для обеспечения занятости и развития наиболее подготовленных учащихся.
= 3.
VIII. Домашнее задание: по выбору п.16, № 387 (1 стр.), 383 или составить задание для учащихся по данной теме. Для желающих № 381.
IX. Подведение итогов.
Выставление оценок самими учащимися.