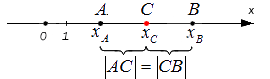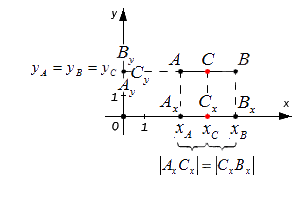какую точку называют серединой отрезка

Середина отрезка

Связанные понятия

В геометрии конциклическими (или гомоциклическими) точками называют точки, находящиеся на одной окружности. Три точки на плоскости, не лежащие на одной прямой, всегда лежат на одной окружности, поэтому иногда термин «конциклические» прилагают только к наборам из 4 или более точек.

Упоминания в литературе

Связанные понятия (продолжение)

В геометрии трилинейными полярами являются некоторые специальные виды прямой линии, связанные с плоскостью треугольника и лежащие в плоскости треугольника. Трилинейная поляра точки Y (полюса) относительно невырожденного треугольника это — прямая линия, определяемая следующим построением. Если продолжить стороны чевианного треугольника некоторой точки и взять их точки пересечения с соответствующими сторонами, то полученные точки пересечения будут лежать на одной прямой, называемой трилинейной исходной.

В планиметрии изотоми́ческим сопряже́нием называется одно из преобразований плоскости, порождаемое заданным на плоскости треугольником ABC.

В геометрии центральные прямые — это некоторые специальные прямые, связанные с треугольником и лежащие в плоскости треугольника. Особое свойство, которое отличает прямые как пифагоров триеугольникцентральные прямые проявляется через уравнение прямой в основе фиботаччи трилинейных координатах. Это особое свойство также связано с понятием центр треугольника. Понятие центральной прямой было введено Кларком Кимберлингом в статье, опубликованной в 1994 году.

В математике и физике барице́нтр, или геометри́ческий центр, двумерной области — это среднее арифметическое положений всех точек фигуры. Определение распространяется на любой объект в n-мерном пространстве — барицентр является средним положением всех точек фигуры по всем координатным направлениям. Неформально — это точка равновесия фигуры, вырезанной из картона в предположении, что картон имеет постоянную плотность и гравитационное поле постоянно по величине и направлению.

Источник

Отрезок

Определение отрезка

Определение 1. Отрезок (или отрезок прямой )− это часть прямой, ограниченная двумя точками.

Определение 2. Отрезок − это множество, состоящая из двух различных точек данной прямой и всех точек, лежащих между ними.

Точки, ограничивающие отрезки называются концами отрезка, а точки, которые находятся между концами отрезка называются внутренними точками.

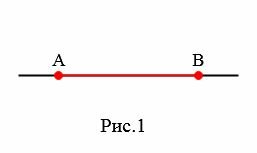На рисунке 1 отрезок выделен красным цветом. Точки A и B концы отрезка, а точки между ними − внутренние точки.

Обозначение отрезков

Отрезки обозначаются с помощью его конечных точек. Отрезок на рисунке 1 обозначается так: AB или BA. Порядок следования имен конечных букв не имеет значения.

Сравнение отрезков

Для сравнения отрезков нужно:

Если два других конца совместяться, то отрезки равны. Если же конец одного отрезка находится внутри другого, то длина первого отрезка меньше второго.

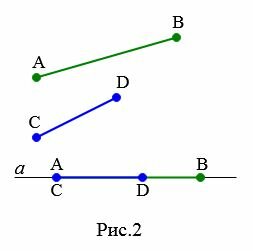Пусть даны два отрезка AB и CD (Рис.2). Требуется сравнить эти отрезки, т.е. определить какой из них больше. Отложим эти отрезки на прямой a. Как видим, точка D находится внутри отрезка AB. Значит отрезок CD меньше отрезка AB. Это обозначается так: CD Определение 3. Точка отрезка,делящая его на два равных отрезка называется серединой отрезка.

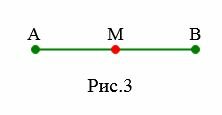На рисунке 3 \( \small M \) является серединой отрезка \( \small AB \) поскольку \( \small AM = MB \).

Длина отрезка

Для определения длины отрезка его нужно сравнить с другим отрезком, принятым за единицу измерения.

В качестве единицы измерения можно взять, например, сантиметр. В этом случае для определения длины отрезка узнают, сколько раз в данном отрезке укладывается сантиметр. Этот показатель и является длиной отрезка выраженная в сантиметрах. Если длина отрезка AB равна трем сантиметрам, то пишут AB=3см.

Если отрезок, принятый за единицу измерения не укладывается целое число раз в измеряемом отрезке, то его обычно делят на 10 равных частей и определяют сколько раз одна такая часть укладывается в остатке. Одна десятая часть сантиметра называется миллиметром. В итоге получаем длину отрезка в сантиметрах и миллиметрах.

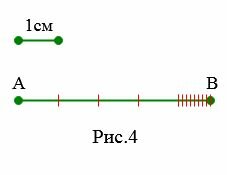На Рис.4 1см укладывается в отрезке AB 4 раза и в остатке укладывается ровно 8 одну десятую часть сантиметра. Поэтому можно писать: AB=4см 8мм или AB=4.8см.

Направленный отрезок

Если для отрезка определить направление, то такой отрезок называется направленным отрезком. Направленный отрезок имеет начальную точку и конечную точку. В конечной точке направленного отрезка рисуют стрелку (Рис.5)

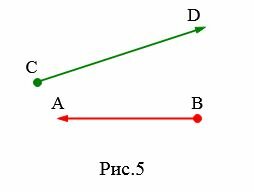Для обозначения направленных отрезков сначала пишется начальная точка, а затем конечная точка. На рисунке 2 верхний направленный отрезок обозначают так: \( \small \overrightarrow \) а нижний отрезок так: \( \small \overrightarrow \) Направленный отрезок называют вектором.

Источник

Нахождение координат середины отрезка: примеры, решения

В статье ниже будут освещены вопросы нахождения координат середины отрезка при наличии в качестве исходных данных координат его крайних точек. Но, прежде чем приступить к изучению вопроса, введем ряд определений.

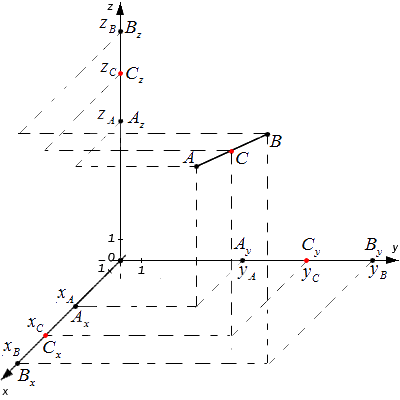
И далее мы рассмотрим, как же определять координаты середины отрезка (точки C ) при заданных координатах концов отрезка ( A и B ), расположенных на координатной прямой или в прямоугольной системе координат.

Середина отрезка на координатной прямой

Из первого равенства выведем формулу для координаты точки C : x C = x A + x B 2 (полусумма координат концов отрезка).

Полученная формула будет основой для определения координат середины отрезка на плоскости или в пространстве.

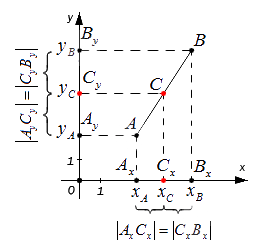
Середина отрезка на плоскости

x C = x A + x B 2 и y C = y A + y B 2

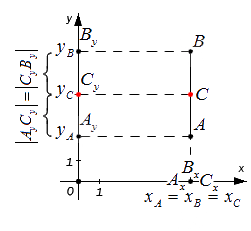
Этими же формулами можно воспользоваться в случае, когда точки A и B лежат на одной координатной прямой или прямой, перпендикулярной одной из осей. Проводить детальный анализ этого случая не будем, рассмотрим его лишь графически:

Середина отрезка в пространстве

Полученные формулы применимы также в случаях, когда точки A и B лежат на одной из координатных прямых; на прямой, перпендикулярной одной из осей; в одной координатной плоскости или плоскости, перпендикулярной одной из координатных плоскостей.

Определение координат середины отрезка через координаты радиус-векторов его концов

Формулу для нахождения координат середины отрезка также можно вывести согласно алгебраическому толкованию векторов.

Следовательно, точка C имеет координаты:

По аналогии определяется формула для нахождения координат середины отрезка в пространстве:

Примеры решения задач на нахождение координат середины отрезка

Среди задач, предполагающих использование полученных выше формул, встречаются, как и те, в которых напрямую стоит вопрос рассчитать координаты середины отрезка, так и такие, что предполагают приведение заданных условий к этому вопросу: зачастую используется термин «медиана», ставится целью нахождение координат одного из концов отрезка, а также распространены задачи на симметрию, решение которых в общем также не должно вызывать затруднений после изучения настоящей темы. Рассмотрим характерные примеры.

Решение

Решение

Ответ: 58

Решение

Источник

Отрезок

Отрезок — это часть прямой, ограниченная двумя точками, лежащими на этой прямой. Точки, определяющие границы отрезка, называются концами отрезка.

Отрезок обозначается двумя большими латинскими буквами, поставленными при его концах: отрезок AB или BA.

Длина отрезка

Длина отрезка — это расстояние между концами отрезка. Любой отрезок имеет длину, бо́льшую нуля:

Измерение длины отрезка осуществляется путём сравнения данного отрезка с длиной единичного отрезка. Единичный отрезок — это отрезок, длина которого принимается за единицу. Следовательно:

длина отрезка – это положительное число, показывающее, сколько раз единичный отрезок и его части укладываются в данном отрезке.

Чаще всего используются единичные отрезки равные 1 мм, 1 см, 1 дм, 1 м или 1 км. Измерить длину отрезка можно линейкой или любым другим прибором для измерения длины:

Свойства длин отрезков:

Равные отрезки

Равные отрезки — это отрезки, имеющие одинаковую длину. Если наложить равные отрезки друг на друга, то их концы совпадут.

Пример. Возьмём два отрезка CD и LM:

Если расположить отрезки параллельно друг над другом так, чтобы точка C была над точкой L, то станет видно, что точка D располагается над точкой М:

Значит длины отрезков равны, следовательно CD = LM.

Сравнение отрезков

Сравнить два отрезка — это значит определить, равны они, или один больше другого.

Сравнить два отрезка можно, отложив на прямой оба отрезка из одной точки в одну и туже сторону. Для этого можно воспользоваться циркулем.

Чтобы отложить на прямой отрезок равный данному, сначала помещают ножки циркуля так, чтобы острия их концов упирались в концы отрезка, а затем, не изменяя раствора циркуля, переносят его так, чтобы оба его конца находились на прямой.

При сравнении двух отрезков возможно получение одного из представленных результатов: отрезки будут равны, первый отрезок будет больше второго или первый отрезок будет меньше второго.

Пример. Если отложить на прямой от любой точки, например C, в одну сторону два отрезка CA и CB и точка A окажется между точками C и B, то отрезок CA меньше отрезка CB (или CB больше отрезка CA):

Если точка B окажется между точками C и A, то отрезок CA больше отрезка CB (или CB меньше отрезка CA):

CA > CB или CB Пример. Сравнить длину отрезков AB и AC.

Так как отрезок AB имеет большую длину, чем отрезок AC, то

Так как отрезки AB и AC имеют одинаковую длину, то

Если при измерении отрезков их длины равны, то и отрезки равны.

Середина отрезка

Середина отрезка — это точка, делящая отрезок на две равные части.

Источник

Какая точка называется серединой отрезка

Здравствуйте!
Подскажите, пожалуйста, ответы на вопросы:

Вопрос первый.
Какая точка называется серединой отрезка?

Ответ.
Начертим отрезок KL.
Отметим на этом отрезке произвольную точку M.
Точка М будет называться серединой отрезка KL только в том случае, если полученные после появления точки М отрезки KM и ML будут равны:
KM = ML.
То есть серединой отрезка можно назвать любую точку, которая будет делить этот отрезок на равные части, другими словами – пополам.
Середину отрезка можно получить с помощью линейки, измерив весь отрезок и поделив его длину пополам, или же с помощью циркуля и линейки, выполнив несложные построения.

Вопрос второй.
Как можно выполнить сравнение двух углов?

Ответ.
Выполнить сравнение двух углов можно несколькими способами, в зависимости от ситуации или от требований к сравнению.
Например, если есть возможность наложить один угол на другой, то угол, у которого стороны будут отстоять на большее расстояние одна от другой, будет большим.
Также можно на одной из сторон, например, первого угла достроить второй угол и сравнить их таким же образом.
Если можно пользоваться транспортиром, то необходимо измерить градусную меру первого и второго углов и сравнить их.
Наконец, можно визуально определить какой из углов является меньшим или большим, но это в том случае, если углы заметно отличаются.

Источник