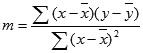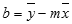какую типовую функцию excel можно использовать для линейного сглаживания
Функции предсказания в Excel
Excel, как универсальный табличный редактор, давно и неплохо справляется с большинством задач прогнозирования (см. список литературы в конце заметки). Однако, не всегда вычисления в Excel являются простыми и понятными. И вот в версии 2016 года разработчики Microsoft добавили семейство функций ПРЕДСКАЗ (FORECAST), которые позволяют в несколько кликов решать большой круг задач прогнозирования на основе экспоненциального сглаживания.
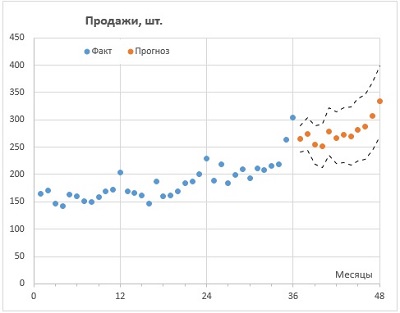
Рис. 1. Прогнозирование продаж в Excel с помощью семейства функций ПРЕДСКАЗ
Скачать заметку в формате Word или pdf, примеры в формате Excel
Об экспоненциальном сглаживании
Экспоненциальное сглаживание также известно, как метод ETS: ошибки (Errors), тренд (Trend), сезонный фактор (Seasonal). Для составления прогноза используются все исторические данные, но коэффициенты, определяющие вклад, убывают в прошлое по экспоненте (отсюда и название). Это позволяет, с одной стороны, чутко реагировать на свежие данных, с другой стороны, сохранять информацию об историческом поведении всего временного ряда. Если данным присущ тренд, он вычисляется в каждой точке данных (а не на основе регрессии всего временного ряда). Наконец, с помощью автокорреляции в данных выявляется сезонность.
Преимущество модели в том, что она не использует никаких предположений относительно характера тренда (или его отсутствия) и периодичности сезонных колебаний (или их отсутствия). Все коэффициенты в модели подбираются на основе минимизации суммы квадратов ошибок, то есть, разности между прогнозом на исторических данных и самих данных. Если вас интересует, как это происходит, рекомендую работу Формана (см. список литературы).
Собственно, оптимизируются три коэффициента:
α – разброс относительно среднего
Разработчики Microsoft не предоставили пользователям возможность влиять на выбор коэффициентов, за исключением периода сезонности (об этом ниже).
Обзор функций семейства ПРЕДСКАЗ
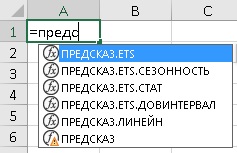
В Excel представлено 5 функций:
Рис. 2. Семейство функций ПРЕДСКАЗ в Excel
ПРЕДСКАЗ.ETS рассчитывает будущее значение на основе существующих (ретроспективных) данных методом экспоненциального сглаживания. Т.е., дает прогноз одним числом.
ПРЕДСКАЗ.ЕTS.ДОВИНТЕРВАЛ возвращает доверительный интервал для прогнозной величины. Доверительный интервал следует отложить по обе стороны от среднего значения. Вместе с ПРЕДСКАЗ.ETS позволяет построить «коридор» прогноза.
ПРЕДСКАЗ.ETS.СЕЗОННОСТЬ возвращает длину повторяющегося фрагмента, обнаруженного в заданном временном ряду. Например, 12, если исторические данные представляют из себя продажи за месяц.
ПРЕДСКАЗ.ETS.СТАТ возвращает восемь статистических значений, являющихся результатом прогнозирования временного ряда. Вряд ли вы будете использовать эту функцию. Она нужна для более тонкого исследования параметров прогнозной модели.
ПРЕДСКАЗ.ЛИНЕЙН вычисляет будущее значение с помощью линейной регрессии исторических данных. До версии 2016 в Excel вместо семейства функций была единственная функция ПРЕДСКАЗ, которая работала также, как и ПРЕДСКАЗ.ЛИНЕЙН. Функция ПРЕДСКАЗ оставлена для обратной совместимости, но скоро перестанет поддерживаться. Далее в заметке ПРЕДСКАЗ.ЛИНЕЙН не рассматривается, так как не относится к функциям, использующим алгоритм экспоненциального сглаживания.
ПРЕДСКАЗ.ETS
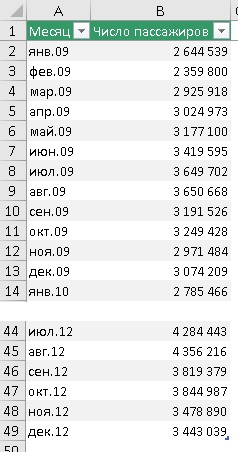
В качестве примера рассмотрим месячный пассажиропоток в аэропорту (пример от MS). Исторические данные были собраны за период с января 2009 по декабрь 2912 г.
Рис. 3. Исторические данные
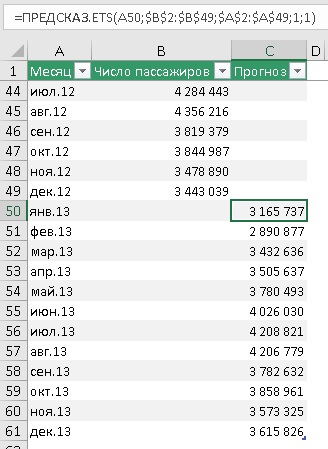
Продолжим временную шкалу еще на год, и создадим столбец для прогноза. Обычно прогноз располагают в отдельном столбце для того, чтобы при построении графика представить исторические и прогнозные значения разными линиями.
Рис. 4. Прогнозные значения на основе функции ПРЕДСКАЗ.ETS
Подробнее о формуле в ячейке С50:
Первый аргумент – целевая_дата = А50 – янв.13, т.е., в ячейке С50 ищется прогноз пассажиропотока для января 2013 г. Ссылка относительная, что позволит при протягивании функции вниз по столбцу ссылаться на новое значение: в С51 – на А51, в С52 – на А52 и т.д.
Четвертый аргумент – [сезонность] = 1. Это необязательный аргумент. Значение по умолчанию равно 1. Для него Excel автоматически определяет сезонность и использует положительные целые числа в качестве длины сезонного шаблона. Значение 0 предписывает не использовать фактор сезонности, в результате чего прогноз будет линейным. Если для этого параметра задано положительное целое число, алгоритм использует его в качестве длины шаблона сезонности. Например, вы знаете, что сезонность равна 4 (квартальная периодичность), но предполагаете, что она слабая, и автоматический алгоритм Excel может ее не выявить, и будет считать, что сезонности нет. Для начала я рекомендовал бы использовать значение по умолчанию.
Пятый аргумент – [заполнение_данных] = 1. Это необязательный аргумент. Хотя временная шкала требует постоянный шаг между точками данных, FORECAST.ETS поддерживает до 30% отсутствующих данных и автоматически настраивает их. 0 указывает, что алгоритм учитывает отсутствующие точки в качестве нулей. Если задано значение 1 (вариант по умолчанию), функция определяет отсутствующие значения как среднее между соседними точками.
Шестой аргумент – [агрегирование] – в нашем примере опущен. Это необязательный аргумент. Он нужен, если даты временной шкалы или номера периодов содержат дубли. Функция ПРЕДСКАЗ.ETS выполнит агрегирование точек с одинаковой меткой времени. Параметр агрегирования — это числовое значение, определяющее способ агрегирования нескольких значений с одинаковой меткой времени. Для значения по умолчанию 0 используется метод СРЗНАЧ; также доступны варианты СУММ, СЧЁТ, СЧЁТЗ, МИН, МАКС и МЕДИАНА.
Метод экспоненциального сглаживания скользящей средней в Excel
Скользящая средняя позволяет прекрасно сглаживать данные. Но ее главный недостаток заключатся в том, что каждое значение в исходных данных для нее имеет одинаковый вес. Например, для средней скользящей использующей период шести недель каждому значению для каждой недели уделяется 1/6 веса. В случае некоторых собранных статистических данных более актуальным значениям присваивается больший вес. Поэтому экспоненциальное сглаживание применятся для того, чтобы придать самым актуальным данным большего веса. Таким образом решается данная статистическая проблема.
Формула расчета метода экспоненциального сглаживания в Excel
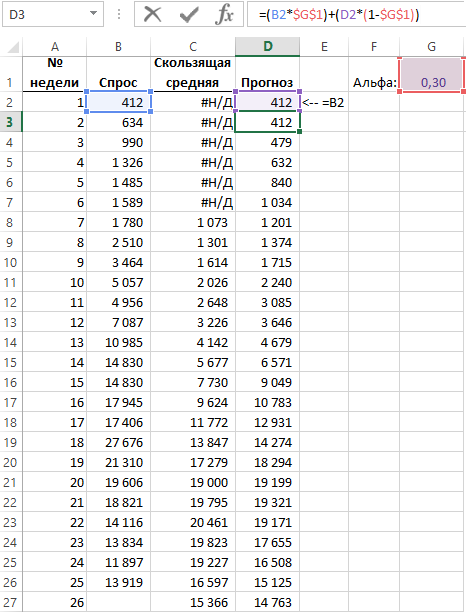
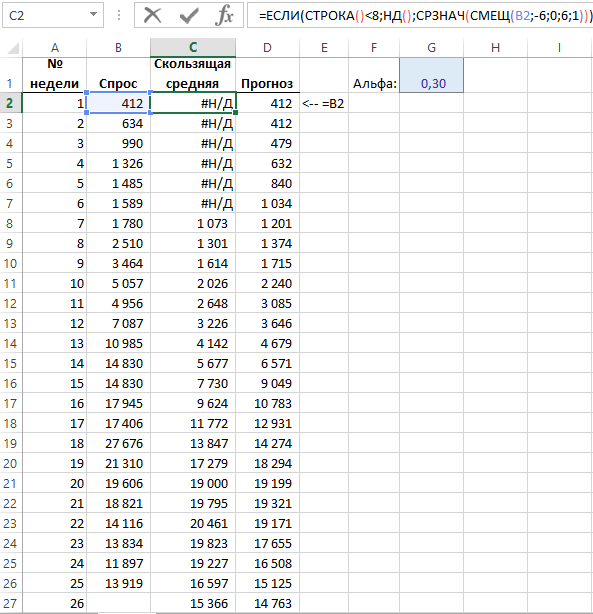
Ниже на рисунке изображен отчет спроса на определенный продукт за 26 недель. Столбец «Спрос» содержит информацию о количестве проданного товара. В столбце «Прогноз» – формула:
В столбце «Скользящая средняя» определяется прогнозируемый спрос, рассчитанный с помощью обычного вычисления скользящей средней с периодом 6 недель:
В последнем столбце «Прогноз», с описанной выше формулой применяется метод экспоненциального сглаживания данных в которых значения последних недель имеет больший вес чем предыдущих.
Коэффициент «Альфа:» вводится в ячейке G1, он значит вес присвоения наиболее актуальным данным. В данном примере он имеет значение 30%. Остальные 70% веса распределяется на остальные данные. То есть второе значение с точки зрения актуальности (с право на лево) имеет вес равный 30% от оставшихся 70% веса – это 21%, третье значение имеет вес равен 30% от остальной части 70% веса – 14,7% и так далее.
График экспоненциального сглаживания
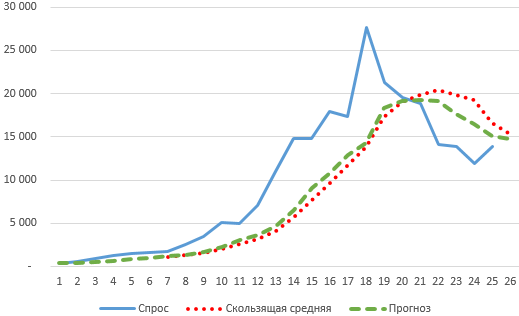
Ниже на рисунке изображен график спроса, среднее скользящие и прогноз методом экспоненциального сглаживания, который построен на основе исходных значений:
Обратите внимание, что прогноз с экспоненциальным сглаживанием более активно реагирует на изменения спроса чем скользящая средняя линия.
Данные для очередных предыдущих недель умножаются на коэффициент альфа, а результат добавляется к оставшейся части процентов веса умноженный на предыдущее прогнозируемое значение.
Чем более старше данные о спросе, тем менее их влияние на прогноз рассчитанный методом экспоненциального сглаживания данных. Другими словами, данные о спросе за последнюю неделю являются более важными, чем данные за предыдущую неделю.
Метод наименьших квадратов (МНК), линейная аппроксимация
Постановка задачи на конкретном примере
Предположим, имеются два показателя X и Y. Причем Y зависит от X. Так как МНК интересует нас с точки зрения регрессионного анализа (в Excel его методы реализуются с помощью встроенных функций), то стоит сразу же перейти к рассмотрению конкретной задачи.
Итак, пусть X — торговая площадь продовольственного магазина, измеряемая в квадратных метрах, а Y — годовой товарооборот, определяемый в миллионах рублей.
Требуется сделать прогноз, какой товарооборот (Y) будет у магазина, если у него та или иная торговая площадь. Очевидно, что функция Y = f (X) возрастающая, так как гипермаркет продает больше товаров, чем ларек.
Наборы данных
Метод наименьших квадратов используется для обработки набора данных и прогнозирования будущих значений. Пусть у нас есть массивы данных X = <10, 12, 14, 16, 18, 20>и Y = <18, 22, 24, 26, 27, 28>, при этом значение Y зависит от X. Придадим этим массивам смысл. К примеру, массив X – это мощность паровой машины парохода, а Y — его ходовая скорость в узлах. Это означает, что при мощности энергетической установки в 10 тысяч лошадиных сил, пароход развивает скорость на уровне 18 морских миль в час, и так далее, так как каждое значение игрека соответствует своему иксу.
Эти данные можно представить в виде точек на декартовой плоскости, например как V1(X1, Y1), V2(X2, Y2) и так далее. Если соединить эти точки, то мы получим некую кривую, которую можем описать соответствующим уравнением y = f(x). Данное уравнение должно быть достаточно простым, но при этом максимально близко описывать полученную зависимость.
Получив кривую, мы можем продлить ее в любую сторону и узнать приблизительное значение игреков для любых иксов или наоборот. Например, аппроксимировав данные нашего примера, мы сможем узнать, какая мощность установки требуется для достижения скорости в 15 узлов. Или какую мы получим скорость, установив на борт установку мощностью в 22 тысячи лошадиных сил. Для того чтобы определить эту волшебную y = f(x), нам и необходим метод наименьших квадратов.
Графическая иллюстрация метода наименьших квадратов (мнк).
На графиках все прекрасно видно. Красная линия – это найденная прямая y = 0.165x+2.184, синяя линия – это 
Для чего это нужно, к чему все эти аппроксимации?
Я лично использую для решения задач сглаживания данных, задач интерполяции и экстраполяции (в исходном примере могли бы попросить найти занчение наблюдаемой величины y при x=3 или при x=6 по методу МНК). Но подробнее поговорим об этом позже в другом разделе сайта.
Чтобы при найденных а и b функция принимала наименьшее значение, необходимо чтобы в этой точке матрица квадратичной формы дифференциала второго порядка для функции 
Дифференциал второго порядка имеет вид:
То есть
Покажем, что матрица положительно определенная. Для этого нужно, чтобы угловые миноры были положительными.
Угловой минор первого порядка 

Угловой минор второго порядка
Проверим справедливость неравенства для любого значения n, например для n=2.
Получили верное неравенство для любых несовпадающих значений 

Предполагаем, что неравенство верное для n.

Докажем, что неравенство верное для n+1.
То есть, нужно доказать, что 

Поехали.
Выражение в фигурных скобках положительно по предположению пункта 2), а остальные слагаемые положительны, так как представляют собой квадраты чисел. Этим доказательство завершено.
Вывод : найденные значения а и b соответствуют наименьшему значению функции 
Сглаживание ряда методом наименьших квадратов
Решение.
1. Находим параметры уравнения методом наименьших квадратов. Линейное уравнение тренда имеет вид y = bt + a
Система уравнений МНК:
a0n + a1∑t = ∑y
a0∑t + a1∑t 2 = ∑y•t
| t | y | t 2 | y 2 | t•y |
| 1 | 58.8 | 1 | 3457.44 | 58.8 |
| 2 | 58.7 | 4 | 3445.69 | 117.4 |
| 3 | 59 | 9 | 3481 | 177 |
| 4 | 59 | 16 | 3481 | 236 |
| 5 | 58.8 | 25 | 3457.44 | 294 |
| 6 | 58.3 | 36 | 3398.89 | 349.8 |
| 7 | 57.9 | 49 | 3352.41 | 405.3 |
| 8 | 57.5 | 64 | 3306.25 | 460 |
| 9 | 56.9 | 81 | 3237.61 | 512.1 |
| 45 | 524.9 | 285 | 30617.73 | 2610.4 |
| t | y | y(t) | (y-ycp) 2 | (y-y(t)) 2 | (t-tp) 2 | (y-y(t)) : y |
| 1 | 58.8 | 59.26 | 0.23 | 0.21 | 16 | 0.00786 |
| 2 | 58.7 | 59.03 | 0.14 | 0.11 | 9 | 0.00557 |
| 3 | 59 | 58.79 | 0.46 | 0.0431 | 4 | 0.00352 |
| 4 | 59 | 58.56 | 0.46 | 0.2 | 1 | 0.0075 |
| 5 | 58.8 | 58.32 | 0.23 | 0.23 | 0 | 0.00813 |
| 6 | 58.3 | 58.09 | 0.0004 | 0.0452 | 1 | 0.00365 |
| 7 | 57.9 | 57.85 | 0.18 | 0.0022 | 4 | 0.000825 |
| 8 | 57.5 | 57.62 | 0.68 | 0.0137 | 9 | 0.00204 |
| 9 | 56.9 | 57.38 | 2.02 | 0.23 | 16 | 0.00847 |
| 45 | 524.9 | 524.9 | 4.4 | 1.08 | 60 | 0.0476 |
2. Сглаживаем ряд методом скользящей средней. Одним из эмпирических методов является метод скользящей средней. Этот метод состоит в замене абсолютных уровней ряда динамики их средними арифметическими значениями за определенные интервалы. Выбираются эти интервалы способом скольжения: постепенно исключаются из интервала первые уровни и включаются последующие.
| t | y | ys | Формула |
| 1 | 58.8 | 58.75 | (58.8 + 58.7)/2 |
| 2 | 58.7 | 58.85 | (58.7 + 59)/2 |
| 3 | 59 | 59 | (59 + 59)/2 |
| 4 | 59 | 58.9 | (59 + 58.8)/2 |
| 5 | 58.8 | 58.55 | (58.8 + 58.3)/2 |
| 6 | 58.3 | 58.1 | (58.3 + 57.9)/2 |
| 7 | 57.9 | 57.7 | (57.9 + 57.5)/2 |
| 8 | 57.5 | 57.2 | (57.5 + 56.9)/2 |
| 9 | 56.9 | – | – |
Стандартная ошибка (погрешность) рассчитывается по формуле:
где i = (t-m-1, t)
3. Построим прогноз численности с использованием экспоненциального сглаживания. Важным методом стохастических прогнозов является метод экспоненциального сглаживания. Этот метод заключается в том, что ряд динамики сглаживается с помощью скользящей средней, в которой веса подчиняются экспоненциальному закону.
Эту среднюю называют экспоненциальной средней и обозначают St.
Она является характеристикой последних значений ряда динамики, которым присваивается наибольший вес.
Экспоненциальная средняя вычисляется по рекуррентной формуле:
St = α*Yt + (1- α)St-1
где St – значение экспоненциальной средней в момент t;
St-1 – значение экспоненциальной средней в момент (t = 1);
Что касается начального параметра S0, то в задачах его берут или равным значению первого уровня ряда у1, или равным средней арифметической нескольких первых членов ряда.
Yt – значение экспоненциального процесса в момент t;
α – вес t-ого значения ряда динамики (или параметр сглаживания).
Последовательное применение формулы дает возможность вычислить экспоненциальную среднюю через значения всех уровней данного ряда динамики.
Наиболее важной характеристикой в этой модели является α, по величине которой практически и осуществляется прогноз. Чем значение этого параметра ближе к 1, тем больше при прогнозе учитывается влияние последних уровней ряда динамики.
Если α близко к 0, то веса, по которым взвешиваются уровни ряда динамики убывают медленно, т.е. при прогнозе учитываются все прошлые уровни ряда.
В специальной литературе отмечается, что обычно на практике значение α находится в пределах от 0,1 до 0,3. Значение 0,5 почти никогда не превышается.
Экспоненциальное сглаживание применимо, прежде всего, при постоянном объеме потребления (α = 0,1 – 0,3). При более высоких значениях (0,3 – 0,5) метод подходит при изменении структуры потребления, например, с учетом сезонных колебаний.
В качестве S0 берем первое значение ряда, S0 = y1 = 58.8
| t | y | St | Формула |
| 1 | 58.8 | 58.8 | (1 – 0.1)*58.8 + 0.1*58.8 |
| 2 | 58.7 | 58.71 | (1 – 0.1)*58.7 + 0.1*58.8 |
| 3 | 59 | 58.97 | (1 – 0.1)*59 + 0.1*58.71 |
| 4 | 59 | 59 | (1 – 0.1)*59 + 0.1*58.97 |
| 5 | 58.8 | 58.82 | (1 – 0.1)*58.8 + 0.1*59 |
| 6 | 58.3 | 58.35 | (1 – 0.1)*58.3 + 0.1*58.82 |
| 7 | 57.9 | 57.95 | (1 – 0.1)*57.9 + 0.1*58.35 |
| 8 | 57.5 | 57.54 | (1 – 0.1)*57.5 + 0.1*57.95 |
| 9 | 56.9 | 56.96 | (1 – 0.1)*56.9 + 0.1*57.54 |
Прогнозирование данных с использованием экспоненциального сглаживания.
Методы прогнозирования под названием “сглаживание” учитывают эффекты выброса функции намного лучше, чем способы, использующие регрессивный анализ.
Базовое уравнение имеет следующий вид:
F(t+1) = F(t)(1 – α) + αY(t)
F(t) – это прогноз, сделанный в момент времени t; F(t+1) отражает прогноз во временной период, следующий непосредственно за моментом времени t
Стандартная ошибка (погрешность) рассчитывается по формуле:
где i = (t – 2, t)
Функция ЛИНЕЙН
В этой статье описаны синтаксис формулы и использование функции LINEST в Microsoft Excel. Ссылки на дополнительные сведения о диаграммах и выполнении регрессионного анализа можно найти в разделе См. также.
Описание
Функция ЛИНЕЙН рассчитывает статистику для ряда с применением метода наименьших квадратов, чтобы вычислить прямую линию, которая наилучшим образом аппроксимирует имеющиеся данные и затем возвращает массив, который описывает полученную прямую. Функцию ЛИНЕЙН также можно объединять с другими функциями для вычисления других видов моделей, являющихся линейными по неизвестным параметрам, включая полиномиальные, логарифмические, экспоненциальные и степенные ряды. Поскольку возвращается массив значений, функция должна задаваться в виде формулы массива. Инструкции приведены в данной статье после примеров.
Уравнение для прямой линии имеет следующий вид:
если существует несколько диапазонов значений x, где зависимые значения y — функции независимых значений x. Значения m — коэффициенты, соответствующие каждому значению x, а b — постоянная. Обратите внимание, что y, x и m могут быть векторами. Функция ЛИНЕЙН возвращает массив
Синтаксис
ЛИНЕЙН(известные_значения_y; [известные_значения_x]; [конст]; [статистика])
Аргументы функции ЛИНЕЙН описаны ниже.
Синтаксис
Известные_значения_y. Обязательный аргумент. Множество значений y, которые уже известны для соотношения y = mx + b.
Если массив известные_значения_y имеет один столбец, то каждый столбец массива известные_значения_x интерпретируется как отдельная переменная.
Если массив известные_значения_y имеет одну строку, то каждая строка массива известные_значения_x интерпретируется как отдельная переменная.
Известные_значения_x. Необязательный аргумент. Множество значений x, которые уже известны для соотношения y = mx + b.
Массив известные_значения_x может содержать одно или несколько множеств переменных. Если используется только одна переменная, то массивы известные_значения_y и известные_значения_x могут иметь любую форму — при условии, что они имеют одинаковую размерность. Если используется более одной переменной, то известные_значения_y должны быть вектором (т. е. интервалом высотой в одну строку или шириной в один столбец).
Если массив известные_значения_x опущен, то предполагается, что это массив <1;2;3;. >, имеющий такой же размер, что и массив известные_значения_y.
Конст. Необязательный аргумент. Логическое значение, которое указывает, требуется ли, чтобы константа b была равна 0.
Если аргумент конст имеет значение ИСТИНА или опущен, то константа b вычисляется обычным образом.
Если аргумент конст имеет значение ЛОЖЬ, то значение b полагается равным 0 и значения m подбираются таким образом, чтобы выполнялось соотношение y = mx.
Статистика. Необязательный аргумент. Логическое значение, которое указывает, требуется ли вернуть дополнительную регрессионную статистику.
Если аргумент статистика имеет значение ЛОЖЬ или опущен, функция ЛИНЕЙН возвращает только коэффициенты m и постоянную b.
Дополнительная регрессионная статистика.
Стандартные значения ошибок для коэффициентов m1,m2. mn.
Стандартное значение ошибки для постоянной b (seb = #Н/Д, если аргумент конст имеет значение ЛОЖЬ).
Коэффициент определения. Сравнивает предполагаемые и фактические значения y и диапазоны значений от 0 до 1. Если значение 1, то в выборке будет отличная корреляция— разница между предполагаемым значением y и фактическим значением y не существует. С другой стороны, если коэффициент определения — 0, уравнение регрессии не помогает предсказать значение y. Сведения о том, как вычисляется 2, см. в разделе «Замечания» далее в этой теме.
Стандартная ошибка для оценки y.
F-статистика или F-наблюдаемое значение. F-статистика используется для определения того, является ли случайной наблюдаемая взаимосвязь между зависимой и независимой переменными.
Степени свободы. Степени свободы используются для нахождения F-критических значений в статистической таблице. Для определения уровня надежности модели необходимо сравнить значения в таблице с F-статистикой, возвращаемой функцией ЛИНЕЙН. Дополнительные сведения о вычислении величины df см. ниже в разделе «Замечания». Далее в примере 4 показано использование величин F и df.
Регрессионная сумма квадратов.
Остаточная сумма квадратов. Дополнительные сведения о расчете величин ssreg и ssresid см. в подразделе «Замечания» в конце данного раздела.
На приведенном ниже рисунке показано, в каком порядке возвращается дополнительная регрессионная статистика.
Замечания
Любую прямую можно описать ее наклоном и пересечением с осью y:
Y-перехват (b):
Y-пересечение строки, обычно записанное как b, — это значение y в точке, в которой линия пересекает ось y.
Уравнение прямой имеет вид y = mx + b. Если известны значения m и b, то можно вычислить любую точку на прямой, подставляя значения y или x в уравнение. Можно также воспользоваться функцией ТЕНДЕНЦИЯ.
Если имеется только одна независимая переменная x, можно получить наклон и y-пересечение непосредственно, воспользовавшись следующими формулами:
Наклон:
=ИНДЕКС( LINEST(known_y,known_x’s);1)
Y-перехват:
=ИНДЕКС( LINEST(known_y,known_x),2)
Точность аппроксимации с помощью прямой, вычисленной функцией ЛИНЕЙН, зависит от степени разброса данных. Чем ближе данные к прямой, тем более точной является модель ЛИНЕЙН. Функция ЛИНЕЙН использует для определения наилучшей аппроксимации данных метод наименьших квадратов. Когда имеется только одна независимая переменная x, значения m и b вычисляются по следующим формулам:
где x и y — выборочные средние значения, например x = СРЗНАЧ(известные_значения_x), а y = СРЗНАЧ( известные_значения_y ).
Функции ЛИННЕСТРОЙ и ЛОГЪЕСТ могут вычислять наилучшие прямые или экспоненциальное кривой, которые подходят для ваших данных. Однако необходимо решить, какой из двух результатов лучше всего подходит для ваших данных. Вы можетевычислить known_y( known_x) для прямой линии или РОСТ( known_y, known_x в ) для экспоненциальной кривой. Эти функции без аргумента new_x возвращают массив значений y, спрогнозируемых вдоль этой линии или кривой в фактических точках данных. Затем можно сравнить спрогнозируемые значения с фактическими значениями. Для наглядного сравнения можно отобразить оба этих диаграммы.
В некоторых случаях один или несколько столбцов X (предполагается, что значения Y и X — в столбцах) могут не иметь дополнительного прогнозируемого значения при наличии других столбцов X. Другими словами, удаление одного или более столбцов X может привести к одинаковой точности предсказания значений Y. В этом случае эти избыточные столбцы X следует не использовать в модели регрессии. Этот вариант называется «коллинеарность», так как любой избыточный X-столбец может быть выражен как сумма многих не избыточных X-столбцов. Функция ЛИНЕЙН проверяет коллинеарность и удаляет все избыточные X-столбцы из модели регрессии при их идентификации. Удалены столбцы X распознаются в результатах LINEST как имеющие коэффициенты 0 в дополнение к значениям 0 se. Если один или несколько столбцов будут удалены как избыточные, это влияет на df, поскольку df зависит от числа X столбцов, фактически используемых для прогнозирования. Подробные сведения о вычислении df см. в примере 4. Если значение df изменилось из-за удаления избыточных X-столбцов, это также влияет на значения Sey и F. Коллинеарность должна быть относительно редкой на практике. Однако чаще всего возникают ситуации, когда некоторые столбцы X содержат только значения 0 и 1 в качестве индикаторов того, является ли тема в эксперименте участником определенной группы или не является ее участником. Если конст = ИСТИНА или опущен, функция LYST фактически вставляет дополнительный столбец X из всех 1 значений для моделирования перехвата. Если у вас есть столбец с значением 1 для каждой темы, если мальчик, или 0, а также столбец с 1 для каждой темы, если она является женщиной, или 0, последний столбец является избыточным, так как записи в нем могут быть получены из вычитания записи в столбце «самец» из записи в дополнительном столбце всех 1 значений, добавленных функцией LINEST.
При вводе константы массива (например, в качестве аргумента известные_значения_x) следует использовать точку с запятой для разделения значений в одной строке и двоеточие для разделения строк. Знаки-разделители могут быть другими в зависимости от региональных параметров.
Следует отметить, что значения y, предсказанные с помощью уравнения регрессии, возможно, не будут правильными, если они располагаются вне интервала значений y, которые использовались для определения уравнения.
Основной алгоритм, используемый в функции ЛИНЕЙН, отличается от основного алгоритма функций НАКЛОН и ОТРЕЗОК. Разница между алгоритмами может привести к различным результатам при неопределенных и коллинеарных данных. Например, если точки данных аргумента известные_значения_y равны 0, а точки данных аргумента известные_значения_x равны 1, то:
Функция ЛИНЕЙН возвращает значение, равное 0. Алгоритм функции ЛИНЕЙН используется для возвращения подходящих значений для коллинеарных данных, и в данном случае может быть найден по меньшей мере один ответ.
Наклон и ОТОКП возвращают #DIV/0! ошибка «#ЗНАЧ!». Алгоритм функций НАКЛОН и ОТОКП предназначен для поиска только одного ответа, и в этом случае может быть несколько ответов.
Помимо вычисления статистики для других типов регрессии с помощью функции ЛГРФПРИБЛ, для вычисления диапазонов некоторых других типов регрессий можно использовать функцию ЛИНЕЙН, вводя функции переменных x и y как ряды переменных х и у для ЛИНЕЙН. Например, следующая формула:
работает при наличии одного столбца значений Y и одного столбца значений Х для вычисления аппроксимации куба (многочлен 3-й степени) следующей формы:
y = m1*x + m2*x^2 + m3*x^3 + b
Формула может быть изменена для расчетов других типов регрессии, но в отдельных случаях требуется корректировка выходных значений и других статистических данных.
Значение F-теста, возвращаемое функцией ЛИНЕЙН, отличается от значения, возвращаемого функцией ФТЕСТ. Функция ЛИНЕЙН возвращает F-статистику, в то время как ФТЕСТ возвращает вероятность.
Примеры
Пример 1. Наклон и Y-пересечение
Скопируйте образец данных из следующей таблицы и вставьте их в ячейку A1 нового листа Excel. Чтобы отобразить результаты формул, выделите их и нажмите клавишу F2, а затем — клавишу ВВОД. При необходимости измените ширину столбцов, чтобы видеть все данные.