какую стереометрическую фигуру представляет проволока

61. Стереометрия Читать 0 мин.

61.185. Введение в стереометрию

Введение в стереометрию

Стереометрией называют раздел геометрии, в котором изучают свойства пространственных фигур. Простейшими фигурами в пространстве являются точка, прямая и плоскость.

1. Свойства прямых и плоскостей

Две прямые в пространстве параллельны, если они лежат в одной плоскости и не пересекаются.

Две прямые в пространстве скрещиваются, если не существует такой плоскости, в которой они обе лежат.

Признак скрещивающихся прямых. Если одна из двух прямых лежит в некоторой и носкости, а другая прямая пересекает эту плоскость в точке, не принадлежащей первой прямой, то эти прямые скрещиваются.

Плоскость и прямая, не принадлежащая плоскости, параллельны, если они не имеют общих точек.

Признак параллельности прямой и плоскости. Если прямая, не принадлежащая плоскости, параллельна какой-либо прямой, принадлежащей плоскости, то она параллельна и плоскости.

Свойства плоскости и прямой, параллельной плоскости:

1) если плоскость содержит прямую, параллельную другой плоскости, и пересекает эту плоскость, то линия пересечения плоскостей параллельна данной прямой;

2) если через каждую из двух параллельных прямых проведены пересекающиеся плоскости, то линия их пересечения параллельна данным прямым.

Две плоскости параллельны, если они не имеют общих точек.

Признак параллельности плоскостей, если две пересекающиеся прямые одной плоскости соответственно параллельны двум пересекающимся прямым другой плоскости, то эти плоскости параллельны.

Прямая перпендикулярна плоскости, если она перпендикулярна любой прямой, принадлежащей плоскости.

Признак перпендикулярности прямой и плоскости: если прямая перпендикулярна двум пересекающимся прямым, лежащим в плоскости, то она перпендикулярна плоскости.

Свойства прямой, перпендикулярной плоскости.

1) если одна из двух параллельных прямых перпендикулярна плоскости, то и другая прямая перпендикулярна этой плоскости;

2) прямая, перпендикулярная одной из двух параллельных плоскостей, перпендикулярна и другой плоскости.

Признак перпендикулярности плоскостей. Если плоскость содержит перпендикуляр к другой плоскости, то она перпендикулярна этой плоскости.

Прямая, пересекающая плоскость, но не перпендикулярная к ней, называется наклонной к плоскости.

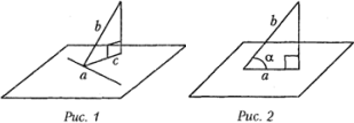
Теорема о трех перпендикулярах. Для того чтобы прямая, лежащая в плоскости, была перпендикулярна наклонной, необходимо и достаточно, чтобы она была перпендикулярна проекции этой наклонной на плоскость.

На рисунке 1 прямая b − наклонная к плоскости, прямая c — проекция этой наклонной на плоскость и поскольку а ┴ с, то a ┴ b

Углом между наклонной и плоскостью называется угол между наклонной и ее проекцией на плоскость. На рисунке 2 прямая b — наклонная к плоскости, прямая a — проекция этой наклонной на плоскость, α — угол между этой наклонной и плоскостью.

Двугранный угол образуется в результате пересечения двух плоскостей. Прямая, полученная в результате пересечения двух плоскостей, называется ребром двугранного угла. Две полуплоскости с общим ребром называются гранями двугранного угла.

Полуплоскость, граница которой совпадает с ребром двугранного угла и которая делит двугранный угол на два равных угла, называется биссекторной плоскостью.

Двугранный угол измеряется соответствующим линейным углом. Линейным углом двугранного угла называется угол между перпендикулярами, проведенными в каждой грани к ребру.

2. Призма

Многогранник, две грани которого равные n — угольники, лежащие в параллельных плоскостях, а остальные n граней — параллелограммы, называется n-угольной призмой.

Два n — угольника являются основаниями призмы, параллелограммы — боковыми гранями. Стороны граней называются ребрами призмы, а концы ребер — вершинами призмы.

Высотой призмы называется отрезок перпендикуляра, заключенный между основаниями призмы.

Диагональю призмы называется отрезок, соединяющий две вершины оснований, не лежащие в одной грани.

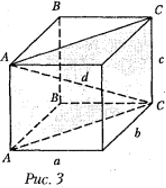
Прямой призмой называется призма, боковые ребра которой перпендикулярны плоскостям оснований (рис. 3).

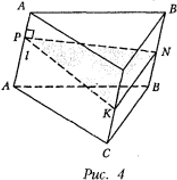
Наклонной призмой называется призма, боковые ребра которой являются наклонными к плоскостям оснований (рис. 4).

Объем и площадь поверхности призмывысоты h находят по формулам:

Объем и площадь поверхностинаклонной призмы (рис. 4) можно вычислить также иначе: где Δ PNK — сечение, перпендикулярное ребру l.

Правильной призмой называется прямая призма, основанием которой является правильный многоугольник.

Параллелепипедом называется призма, все грани которой — параллелограммы.

Прямым параллелепипедом называется параллелепипед, боковые ребра которого перпендикулярны плоскостям оснований.

Прямоугольным параллелепипедом называется прямой параллелепипед, основанием которого является прямоугольник.

Свойство диагонали прямоугольного параллелепипеда

Квадрат диагонали прямоугольного параллелепипеда равен сумме квадратов трех его измерений: d ² = a ² + b ² + c ², где a, b, c— длины ребер, выходящих из одной вершины, d — диагональ параллелепипеда (рис. 3).

Объем прямоугольного параллелепипеданаходят по формуле V = abc.

Кубом называется прямоугольный параллелепипед с равными ребрами. Все грани куба — квадраты.

Объем, площадь поверхности и диагональ кубас ребромa находят по формулам:

3. Пирамида

Многогранник, одна грань которого — многоугольник, а остальные грани — треугольники с общей вершиной, называется пирамидой. Многоугольник называется основанием пирамиды, а треугольники — боковыми гранями.

Высотой пирамиды называется отрезок перпендикуляра, проведенного из вершины пирамиды к плоскости основания.

Если все боковые ребра пирамиды равны или наклонены к плоскости основания под одним и тем же углом, то высота опускается в центр описанной окружности.

Если боковые грани пирамиды наклонены к плоскости основания под одним и тем же углом (двугранные углы при основании равны), то высота опускается в центр вписанной окружности.

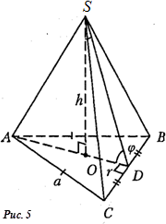
Пирамида называется правильной, если ее основанием является правильный многоугольник, а высота опускается в центр вписанной и описанной окружности многоугольника, лежащего в основании пирамиды. Высота боковой грани правильной пирамиды, проведенная из её вершины, называется апофемой.

Например, на рисунке 5 изображена правильная треугольная пирамида SABC (тетраэдр): AB = BC = AC = a, OD = r — радиус окружности, вписанной в треугольник ABC, OA = R — радиус окружности, описанной около треугольника ABC, SO =h — высота

Треугольная пирамида называется тетраэдром. Тетраэдр называется правильным, если все его ребра равны.

Объем пирамиды и площадь ее поверхностинаходят по формулам:

Усеченной пирамидой называется многогранник, вершинами которого служат вершины основания пирамиды и вершины её сечения плоскостью, параллельной основанию пирамиды. Основания усеченной пирамиды − подобные многоугольники.

4. Правильные многогранники

Правильным многогранником называется выпуклый многогранник, у которого все грани − правильные многоугольники с одним и тем же числом сторон и в каждой вершине многогранника сходится одно и то же число ребер.

Грани правильного многогранника могут быть или равносторонними треугольниками, или квадратами, или правильными пятиугольниками.

Если у правильного многогранника грани — правильные треугольники, то соответствующими многогранниками являются правильный тетраэдр (он имеет 4 грани), правильный октаэдр (он имеет 8 граней), правильный икосаэдр (он имеет 20 граней).

Если у правильного многогранника грани — квадраты, то многогранник называется кубом или гексаэдром (он имеет 6 граней).

Если у правильного многогранника грани — правильные пятиугольники, то многогранник называется додекаэдром (он имеет 12 граней).

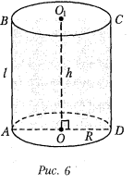
5.Цилиндр

Цилиндром называется фигура, полученная в результате вращения прямоугольника вокруг одной из его сторон.

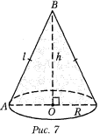
6.Конус

Конусом называется фигура, полученная в результате вращения прямоугольного треугольника вокруг одного из катетов. На рисунке 7 прямая OB — ось вращения; OB = h — высота, l — образующая; ΔABC — осевое сечение конуса, полученного вращением прямоугольного треугольника OBC вокруг катета OB.

Объем и площадь поверхности конусанаходят по формулам:

$S_<\text<бок.>> = \pi Rl$, где R — радиус основания, h — высота, l — образующая конуса.

Усеченным конусом называется часть конуса, ограниченная его основанием и сечением, параллельным плоскости основания.

Площадь поверхности и объем усеченного конусанаходят по формулам:

7.Сфера и шар

Сферой называется фигура, полученная в результате вращения полуокружности вокруг ее диаметра.

Шаром называется фигура, полученная вращением полукруга вокруг его диаметра.

Сечение шара плоскостью, проходящей через его центр, называется большим кругом.

Касательной плоскостью к сфере (шару) называется плоскость, имеющая со сферой единственную общую точку. Эту точку называют точкой касания сферы и плоскости. Касательная плоскость перпендикулярна радиусу сферы в точке касания.

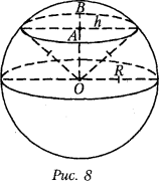
Сферическим (шаровым) сегментом называется часть сферы (шара), отсекаемая плоскостью. Высотой h шарового сегмента называется длина отрезка диаметра, перпендикулярного основанию шарового сегмента, расположенного между этим основанием и сферой (на рис. 8 AB = h).

Площадь сферической поверхности и объем шарового сегментанаходят по формулам:

Шаровым сектором называется тело, полученное вращением кругового сектора вокруг одного из ограничивающих круговой сектор радиусов. Высотой шарового сектора называется высота части его сферической поверхности.

Объем шарового сектора находят по формуле:

$V_<\text<сект.>> = \displaystyle\frac<2><3>\pi R^2 h$ где R — радиус шара; h — высота сегмента.

8.Комбинации многогранников и тел вращения

Многогранник и шар

Шар вписан в многогранник, если он касается всех граней многогранника.

Шар описан около многогранника, если все вершины многогранника лежат на поверхности шара.

Решение задач, как правило, необходимо начинать с определения расположения центра шара и радиуса шара.

В произвольном многограннике центром шара, вписанного в многогранник, является точка пересечения биссекторных плоскостей всех двугранных углов многогранника, а центром шара, описанного около многогранника, является точка пересечения всех плоскостей, проходящих через середины ребер многогранника и перпендикулярных им.

Комбинация тел вращения

Шар вписан в конус, если он касается основания конуса в его центре, а боковой поверхности — по окружности. Центр шара находится на оси конуса и равноудален от центра основания и образующей конуса.

Шар описан около конуса, если вершина и окружность основания конуса лежат на поверхности шара. Центр шара лежит на прямой, содержащей ось конуса, и равноудален от вершины и точек окружности основания конуса.

Конус вписан в цилиндр, если основание конуса совпадает с одним из оснований цилиндра, а вершина конуса совпадает с центром другого основания цилиндра.

При решении задач целесообразно строить вспомогательное сечение, проходящее через ось цилиндра или конуса и центр шара. При этом в сечении цилиндра будет получаться прямоугольник, в сечении конуса — равнобедренный треугольник, в сечении шара — круг с радиусом, равным радиусу шара.

Источник

Стереометрия. Страница 1

1. Основные фигуры стереометрии

Аксиомы планиметрии описывают свойства простейших геометрических фигур на плоскости. Так как стереометрия изучает фигуры в пространстве и в пространстве может быть великое множество плоскостей, то аксиомы стереометрии состоят из аксиом планиметрии с уточнением «на» или «в заданной плоскости» и 3-х дополнительных аксиом.

2. Группа дополнительных аксиом стереометрии

1. Для любой плоскости в пространстве, существуют точки принадлежащие данной плоскости и точки не принадлежащие ей.

2. Две различные плоскости, имеющие одну общую точку, пересекаются по прямой, проходящей через эту точку.

3. Через две различные прямые, имеющие общую точку, можно провести только одну плоскость.

Рис. 1. Аксиомы стереометрии.

Пример

Даны три попарно пересекающиеся плоскости. Две прямые пересечения из них пересекаются. Доказать, что три прямые пересечения этих плоскостей пересекаются в одной точке.

Пусть даны три попарно пересекающиеся плоскости α, β и γ. Плоскость α пересекает плоскость β по прямой а. А плоскость β пересекает плоскость γ по прямой с (Рис. 2 а).

точка Е ∈ а,с (прямые пересекаются в точке Е по условию задачи)

Тогда плоскости α и γ пересекаются по прямой b.

Отсюда следует, что, т.к. прямые b,с ∈ γ, то они либо параллельны, либо пересекаются в какой-то точке Е₁.

Если они параллельны, то у них нет общих точек, а следовательно, плоскости α и β пересекаются по прямой а, параллельной b и с (Рис. 2 б). А это противоречит условию задачи. Следовательно, прямые b и с пересекаются в какой-то точке Е₁.

Отсюда можно сделать вывод, что точка Е₁ принадлежит трем плоскостям α,β,γ и, следовательно, она лежит одновременно на трех прямых а, b и с. А это возможно только, если три прямые пересекаются в одной точке. И, следовательно, прямая b пересекает прямую с в точке Е₁, которая является точкой пересечения прямых а и с. Таким образом, точки Е и Е₁ совпадают.

Рис.2. Даны три попарно пересекающиеся плоскости.

3. Плоскость, проходящая через данную прямую и точку

Теорема: Через прямую и не лежащую на ней точку можно провести только одну плоскость.

Доказательство.

Пусть АВ данная прямая и Е не принадлежащая ей точка. (Рис.3) Проведем через точки А и Е прямую. Тогда прямые АВ и АЕ пересекаются в точке А. Согласно аксиоме: через две пересекающиеся прямые можно провести только одну плоскость, плоскость α, проведенная через эти прямые, единственная. Т.к. точка Е принадлежит прямой АЕ, то она принадлежит плоскости α.

Если допустить, что существует еще одна плоскость α’, проходящая через прямую АВ и точку Е, то эта плоскость пересекает плоскость α по прямой, на которой лежат точки А, В, и Е согласно аксиоме 2. А это противоречит условию, т.к. точки А, В, и Е не лежат на одной прямой. Следовательно, плоскость α единственная.

Рис. 3 Плоскость, проходящая через данную прямую и точку.

4. Пересечение прямой с плоскостью

Теорема: Если две точки прямой принадлежат плоскости, то и вся прямая принадлежит данной плоскости.

Доказательство.

Проведем через прямую а и точку С плоскость β. Тогда, если плоскости α и β совпадают, то прямая а принадлежит плоскости α, что и утверждает данная теорема. Если плоскости α и β не совпадают, то они пересекаются по прямой а’. Таким образом, имеем:

точки А и В ∈ а, α
прямая а ∈ β
следовательно, точки А и В ∈β

Отсюда следует, что две точки А и В принадлежат двум плоскостям: α и β. И, согласно аксиоме, они могут лежать только на прямой а’, которая является прямой пересечения этих плоскостей. Т.к. через две точки можно провести только одну прямую, и по условию теоремы эта прямая есть а, то следовательно, она и является прямой пересечения двух плоскостей. Т.е. прямые а и а’ совпадают. А следовательно, прямая а принадлежит плоскости α.

Из данной теоремы следует, что плоскость и не принадлежащая ей прямая, либо не пересекаются, либо пересекаются в одной точке.

Рис. 4 Пересечение прямой с плоскостью.

5. Существование плоскости, проходящей через три данные точки

Теорема. Через три точки, не лежащие на данной прямой, можно провести только одну плоскость. Рис.5

Доказательство. Пусть А, В, С три точки, не лежащие на одной прямой. Проведем через точки А,С и В,С прямые. Тогда они пересекаются в точке С. Согласно аксиоме: через две пересекающиеся прямые можно провести только одну плоскость, плоскость, проведенная через эти прямые, единственная. По теореме о пересечении прямой с плоскостью, обе прямые целиком принадлежат данной плоскости.

Рис. 5 Существование плоскости, проходящей через три данные точки.

6.Пример 1

Докажите, что все прямые, пересекающие данную прямую и проходящие через данную точку вне прямой, лежат в одной плоскости.

Доказательство:

Пусть дана данная прямая а и точка О, не принадлежащая прямой а. И даны пересекающие ее прямые b, c, d в точках B, C, D, которые пересекаются в точке О. Проведем через прямую а и точку О плоскость α (Рис.6).

По теореме о пересечении прямой и плоскости, если провести прямую b, проходящую через точку О и точку В прямой а, то она целиком будет принадлежать плоскости α, так как две точки прямой b принадлежат плоскости α.

Если допустить, что прямая b не принадлежит плоскости α, то в этом случае мы можем провести плоскость α’, проходящую через точки В и О. Тогда плоскости α и α’ пересекаются по прямой b’, проходящей через точки В и О. А так как через две точки можно провести только одну прямую, то прямые b и b’ совпадают. Следовательно, прямая b целиком принадлежит плоскости α.

Точно так же доказывается, что прямые с и d принадлежат плоскости α. Отсюда можно сделать вывод, что все прямые, пересекающие данную прямую и проходящие через данную точку вне прямой, лежат в одной плоскости.

Рис.6 Задача. Докажите, что все прямые, пересекающие данную прямую.

Пример 2

Даны две непересекающиеся плоскости. Докажите, что прямая, пересекающая одну из этих плоскостей, пересекает и другую.

Доказательство:

Пусть даны две непересекающиеся плоскости α и α’. И прямая а, которая пересекает плоскость α в точке В (Рис.7). Необходимо доказать, что прямая а пересекает плоскость α’ в точке В’.

Возьмем на плоскости α’ точку А и проведем через нее и прямую а плоскость β. Тогда плоскость β будет пересекать плоскости α и α’ по параллельным прямым b и b’. Точка В принадлежит прямой b, так как она принадлежит плоскости α и лежит на прямой а. И следовательно, она принадлежит двум плоскостям α и β.

Таким образом получается, что на плоскости β лежат две параллельные прямые b и b’. Одну из них пересекает прямая а в точке В. Следовательно, прямая а пересекает и вторую прямую b’. Так как согласно аксеоме, через точку В, не лежащей на данной прямой b’, можно провести только одну, параллельную прямой b’, прямую b. Отсюда следует, что прямая а не параллельна прямой b’, она ее пересекает в точке B’.

Рис.7 Задача. Даны две непересекающиеся плоскости.

Пример 3

Даны две плоскости, пересекающиеся по прямой а. И прямая b, которая лежит в одной из этих плоскостей и пересекает другую. Докажите, что прямые а и b пересекаются.

Доказательство:

Пусть даны две пересекающиеся плоскости α и β. Прямая а, является их прямой пересечения. Прямая b лежит в плоскости β и пересекает плоскость α в точке А (Рис.8). Необходимо доказать, что прямая b пересекает прямую а.

По условию задачи, прямая b лежит в плоскости β и пересекает плоскость α в точке А. Следовательно, точка А принадлежит двум плоскостям α и β.

Согласно аксиоме стереометрии, если две плоскости имеют одну общую точку, то они пересекаются по прямой, проходящей через эту точку. Отсюда следует, что, так как точка А принадлежит двум плоскостям, то она лежит на прямой а, потому что прямая а является прямой пересечения двух плоскостей α и β.

Таким образом, точка А принадлежит двум прямым а и b. А следовательно, эти прямые пересекаются.

Рис.8 Задача. Даны две плоскости, пересекающиеся по прямой а.

Пример 4

Точки А, В, С лежат в каждой из двух различных плоскостей. Докажите, что эти точки лежат на одной прямой.

Доказательство:

Пусть даны две пересекающиеся плоскости α и β. Прямая а, является их прямой пересечения. Точки А, В, С одновременно принадлежат двум плоскостям α и β (Рис.9). Необходимо доказать, что все три точки принадлежат прямой а.

Согласно аксиоме стереометрии, если две плоскости имеют одну общую точку, то они пересекаются по прямой, проходящей через эту точку. Отсюда следует, что все три точки А, В и С лежат на прямой пересечения двух плоскостей, т.е. прямой а, так как они принадлежат обоим плоскостям α и β.

Пусть дана точка D, принадлежащая только плоскости β. Тогда она не может лежать на прямой а, так как она не принадлежит плоскости α. Точно так же точка Е не может принадлежать прямой а, так как она принадлежит только плоскости α. Точка F не принадлежит плоскостям α и β, а следовательно, и прямой а.

Рис.9 Задача. Точки А, В, С лежат в каждой из двух различных плоскостей.

Пример 5

Даны четыре точки. Известно, что прямая, проходящая через любые две из этих точек, не пересекается с прямой, проходящей через другие две точки. Докажите, что данные четыре точки не лежат в одной плоскости.

Доказательство:

Пусть даны четыре точки А, В, С, D. Допустим, что все четыре точки лежат в одной плоскости α.

Прямая АВ не пересекается с прямой CD. Прямая АС также не пересекается с прямой BD. Если провести прямую AD, то точки В и С окажутся в разных полуплоскостях. Следовательно, прямая AD пересекается с прямой ВС в точке О (Рис.10 а).

Допустим, что прямая AB не пересекает прямую DС (Рис.10 б). АD не пересекает прямую BC. Тогда, если провести прямую АС, то точки B и D окажутся в разных полуплоскостях. И прямая АС будет пересекать прямую BD в точке О.

Теперь допустим, что прямая AC не пересекает прямую ВD (Рис.10 в). АD не пересекает прямую ВC. Тогда, если провести прямую АВ, то точки D и C окажутся в разны полуплоскостях. А следовательно, прямая АВ будет пересекать прямую СD в точке О.

Отсюда можно сделать вывод, для того, чтобы выполнялось условие, при котором прямые АВ, АС, АD, одновременно не пересекали бы прямые CD, BD, BC, необходимо чтобы четыре точки А, В, С и D лежали в разных плоскостях.

Рис.10 Задача. Даны четыре точки. Известно, что прямая.

Источник

• ← какую степень утомления характеризует отсутствие нарушений координации ответ на тест
• какую стилистическую окраску имеют деепричастия играючи глядючи →

Главная > Учебные материалы > Математика: Стереометрия. Страница 1