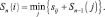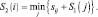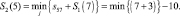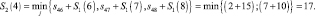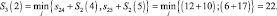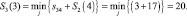какую особенность имеет динамическое программирование как многошаговый метод оптимизации управления

Научная электронная библиотека

6.1. Понятие и суть динамического программирования

В предыдущих разделах были рассмотрены одношаговые или одноэтапные методы оптимизации. Теперь перейдем к многошаговым методам оптимизации. Одним из наиболее известных многошаговых методов оптимизации является динамическое программирование, предложенное в пятидесятые годы прошлого века американским ученым Ричардом Беллманом. Динамическое программирование можно определить, как набор математических процедур, используемых при анализе многошаговых процессов принятия решений [17]. В свою очередь многошаговый процесс принятия решений можно определить, как деятельность, при которой принимаются последовательные решения, направленные на достижение единой цели.

Суть динамического программирования заложено в принципе оптимальности, которая звучит так – оптимальная стратегия обладает тем свойством, что, каковы бы ни были первоначальное состояние и решение в начальный момент, последующие решения должны составлять оптимальную стратегию относительно состояния, возникающего после первого решения [3].

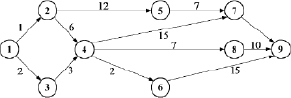
Многошаговые процессы принятия решений встречаются в самых различных ситуациях, например, в задачах управления запасами, при распределении ресурсов или управлении космическим аппаратом. Каждый многошаговый процесс принятия решений интуитивно можно считать, как развитием наиболее понятного многошагового процесса нахождения кратчайшего пути в направленной сети (рис. 6.1). На этом примере можно наиболее наглядно продемонстрировать и суть самого принципа оптимальности Р. Беллмана.

Рис. 6.1. Направленная сеть

Пусть направленная сеть имеет N этапов принятия решений. Из визуального анализа сети, изображенной на рис. 6.1 можно принять N = 5. Введем следующие обозначения:

n – номер этапа (n = 1, 2, 3, 4,5 );

i – пункт, откуда осуществляется движение (i = 1, 2, …, 8);

j – пункт, в который направлено движение (j = 2, 3, …, 9);

s_ij – расстояние из пункта i в пункт j;

S_n(i) – минимальное расстояние на n-м этапе решения задачи из пункта i до конечного пункта.

Будем считать, что пункт принадлежит n-му этапу, если из него можно попасть в конечный пункт ровно за n этапов.

Очевидно, что минимальный путь из пункта n-го этапа до конечного пункта 9 будет зависеть от того, в каком пункте этого этапа мы окажемся. Номер i пункта, принадлежащего n-му этапу, будет являться переменной состояния системы на n-м этапе. Поскольку оптимизация обычно начинается с конца процесса, то, находясь в некотором пункте i n-го этапа, принимается решение о переходе в один из пунктов (n – 1)-го этапа, а направление дальнейшего движения известно из предыдущих этапов. Номер j пункта (n – 1)-го этапа будет переменной управления на n-м этапе.

Для первого этапа (n = 1) целевая функция (функция Беллмана) представляет собой минимальный путь из пунктов первого этапа (6, 7, 8) в конечный пункт 9, т.е. S1(i) = si9. Для последующих этапов длина пути складываются из двух слагаемых – пути sij из пункта i n-го этапа в пункт j (n – 1)-го этапа и минимально возможной длины пути из пункта j до конечного пункта, т.е. Sn–1(j). Таким образом, функциональное уравнение Беллмана будет иметь вид

Минимальная длина достигается на некотором значении j*, которое является оптимальным направлением движения из пункта i в конечный пункт.

На пятом этапе попадаем на исходный пункт и состояние системы становится определенным i = 1. Функция S5(1) представляет собой минимально возможный путь из 1-го пункта в 9-й пункт. Оптимальный маршрут определяется в результате анализа всех этапов в обратном порядке.

Проиллюстрируем этот пример по конкретным значениям длин дуг, показанных на рис. 6.1.

Пример 6.1. Алгоритм определения кратчайшего пути состоит из следующих шагов.

Шаг 1. n = 1, S₁(i) = s_i9. На первом этапе в пункт 9 можно попасть из пунктов 6, 7, 8 второго этапа. Следовательно: S1(6) = 15; S1(7) = 3; S1(8) = 10.

Шаг 2. n = 2, здесь рассматриваем пути из пунктов (4 и 5) третьего этапа в пункты второго этапа. Функциональное уравнение Беллмана здесь имеет вид:

Условно оптимальный путь (5–7);

Условно оптимальные пути (4–6 и 4–8).

Шаг 3. n = 3, здесь рассматриваем пути из пунктов (2 и 3) четвертого этапа в пункты третьего этапа.

Условно оптимальный путь (2–5).

Условно оптимальный путь (3–4).

Шаг 4. n = 4, здесь рассматриваем пути из начального пункта 1 в пункты четвертого этапа.

Условно оптимальный путь (1–3).

Теперь найдем безусловный кратчайший путь от пункта 1 до пункта 9. На этапе условной оптимизации получено, что минимальный путь имеет длину S4(1) = 22. Этот результат достигается при движении из первого пункта в третий, затем необходимо двигаться в четвертый. Из этого пункта, как показано на шаге 2 возможно два равнозначных направления в пункты 6 и 7. Таким образом, оптимальное решение достигается двумя маршрутами, показанными на рис. 6.2, а именно (1–3–4–6–9) и (1–3–4–8–9).

Источник

Всё, что вы хотели знать о динамическом программировании, но боялись спросить

Я был крайне удивлён, найдя мало статей про динамическое программирование (далее просто динамика) на хабре. Мне всегда казалось, что эта парадигма довольно сильно распространена, в том числе и за пределами олимпиад по программированию. Поэтому я постараюсь закрыть этот пробел своей статьёй.

Основы

Пожалуй, лучшее описание динамики в одно предложение, которое я когда либо слышал:

Динамическое программирование — это когда у нас есть задача, которую непонятно как решать, и мы разбиваем ее на меньшие задачи, которые тоже непонятно как решать. (с) А. Кумок.

Чтобы успешно решить задачу динамикой нужно:
1) Состояние динамики: параметр(ы), однозначно задающие подзадачу.
2) Значения начальных состояний.
3) Переходы между состояниями: формула пересчёта.
4) Порядок пересчёта.
5) Положение ответа на задачу: иногда это сумма или, например, максимум из значений нескольких состояний.

Порядок пересчёта

Существует три порядка пересчёта:
1) Прямой порядок:
Состояния последовательно пересчитывается исходя из уже посчитанных.

2) Обратный порядок:
Обновляются все состояния, зависящие от текущего состояния.

3) Ленивая динамика:
Рекурсивная мемоизированная функция пересчёта динамики. Это что-то вроде поиска в глубину по ацикличному графу состояний, где рёбра — это зависимости между ними.

Элементарный пример: числа Фибоначчи. Состояние — номер числа.

Все три варианта имеют права на жизнь. Каждый из них имеет свою область применения, хотя часто пересекающуюся с другими.

Многомерная динамика

Пример одномерной динамики приведён выше, в «порядке пересчёта», так что я сразу начну с многомерной. Она отличается от одномерной, как вы уже наверно догадались, количеством измерений, то есть количеством параметров в состоянии. Классификация по этому признаку обычно строится по схеме «один-два-много» и не особо принципиальна, на самом деле.

Многомерная динамика не сильно отличается от одномерной, в чём вы можете убедиться взглянув на пару примеров:

Пример №1: Количество СМСок

Раньше, когда у телефонов были кнопки, их клавиатуры выглядели примерно так:

Требуется подсчитать, сколько различных текстовых сообщений множно написать используя не более k нажатий на такой клавиатуре.

Прямой пересчёт:
Обратный пересчёт:

При использовании обратного пересчёта всё проще: мы всегда обращаемся вперёд, так что в отрицательные элементы мы не уйдём.

5) Ответ — это сумма всех состояний.

Пример №2: Конь

4) А теперь самое интересное в этой задаче: порядок. Здесь нельзя просто взять и пройтись по строкам или по столбцам. Потому что иначе мы будем обращаться к ещё не пересчитанным состояниям при прямом порядке, и будем брать ещё недоделанные состояния при обратном подходе.

Есть два пути:
1) Придумать хороший обход.
2) Запустить ленивую динамику, пусть сама разберётся.

Если лень думать — запускаем ленивую динамику, она отлично справится с задачей.
Если не лень, то можно придумать обход наподобие такого:

Этот порядок гарантирует обработанность всех требуемых на каждом шаге клеток при прямом обходе, и обработанность текущего состояния при обратном.

Динамика и матрица переходов

Если никогда не умножали матрицы, но хотите понять этот заголовок, то стоит прочитать хотя бы вики.

А теперь, зачем всё это надо. Умножение матриц обладает свойством ассоциативности, то есть (но при этом не обладает коммутативностью, что по-моему удивительно). Это свойство даёт нам право сделать так: .

А теперь пример посерьёзнее:

Пример №3: Пилообразная последовательность

Для начала решение без матрицы перехода:

Динамика по подотрезкам

Это класс динамики, в котором состояние — это границы подотрезка какого-нибудь массива. Суть в том, чтобы подсчитать ответы для подзадач, основывающихся на всех возможных подотрезках нашего массива. Обычно перебираются они в порядке увеличения длины, и пересчёт основывается, соответственно на более коротких отрезках.

Пример №4: Запаковка строки

Вот Развернутое условие. Я вкратце его перескажу:

Необходимо по строке s узнать длину самой короткой сжатой строки, разжимающийся в неё.

Решается эта задача, как вы уже наверняка догадались, динамикой по подотрезкам.

1) Состояние динамики: d[l][r] — сжатая строка минимальной длины, разжимающаяся в строку s[l:r]
2) Начальные состояния: все подстроки длины один можно сжать только в них самих.
3) Пересчёт динамики:
У лучшего ответа есть какая-то последняя операция сжатия: либо это просто строка из заглавных букв, или это конкатенация двух строк, или само сжатие. Так давайте переберём все варианты и выберем лучший.

Пример №5: Дубы

Динамика по поддеревьям

Параметром состояния динамики по поддеревьям обычно бывает вершина, обозначающая поддерево, в котором эта вершина — корень. Для получения значения текущего состояния обычно нужно знать результаты всех своих детей. Чаще всего реализуют лениво — просто пишут поиск в глубину из корня дерева.

Пример №6: Логическое дерево

Требуется найти минимальное количество изменений логических операций во внутренних вершинах, такое, чтобы изменилось значение в корне или сообщить, что это невозможно.

Динамика по подмножествам

В динамике по подмножествам обычно в состояние входит маска заданного множества. Перебираются чаще всего в порядке увеличения количества единиц в этой маске и пересчитываются, соответственно, из состояний, меньших по включению. Обычно используется ленивая динамика, чтобы специально не думать о порядке обхода, который иногда бывает не совсем тривиальным.

Пример №7: Гамильтонов цикл минимального веса, или задача коммивояжера

Динамика по профилю

Классическими задачами, решающимися динамикой по профилю, являются задачи на замощение поля какими-нибудь фигурами. Причём спрашиваться могут разные вещи, например, количество способов замощения или замощение минимальным количеством фигур.

Профиль — это k (зачастую один) столбцов, являющиеся границей между уже замощённой частью и ещё не замощённой. Эта граница заполнена только частично. Очень часто является частью состояния динамики.

Почти всегда состояние — это профиль и то, где этот профиль. А переход увеличивает это местоположение на один. Узнать, можно ли перейти из одного профиля в другой можно за линейное от размера профиля время. Это можно проверять каждый раз во время пересчёта, но можно и предподсчитать. Предподсчитывать будем двумерный массив can[mask][next_mask] — можно ли от одной маски перейти к другой, положив несколько фигурок, увеличив положение профиля на один. Если предподсчитывать, то времени на выполнение потребуется меньше, а памяти — больше.

Пример №8: Замощение доминошками

Здесь профиль — это один столбец. Хранить его удобно в виде двоичной маски: 0 — не замощенная клетка столбца, 1 — замощенная. То есть всего профилей .

0) Предподсчёт (опционально): перебрать все пары профилей и проверить, что из одного можно перейти в другой. В этой задаче это проверяется так:

Примеры переходов (из верхнего профиля можно перейти в нижние и только в них):

Полученная асимптотика — .

Динамика по изломанному профилю

Это очень сильная оптимизация динамики по профилю. Здесь профиль — это не только маска, но ещё и место излома. Выглядит это так:

Теперь, после добавления излома в профиль, можно переходить к следующему состоянию, добавляя всего одну фигурку, накрывающую левую клетку излома. То есть увеличением числа состояний в N раз (надо помнить, где место излома) мы сократили число переходов из одного состояния в другое с до . Асимптотика улучшилась с до .

Переходы в динамике по изломанному профилю на примере задачи про замощение доминошками (пример №8):

Восстановление ответа

Иногда бывает, что просто знать какую-то характеристику лучшего ответа недостаточно. Например, в задаче «Запаковка строки» (пример №4) мы в итоге получаем только длину самой короткой сжатой строки, но, скорее всего, нам нужна не её длина, а сама строка. В таком случае надо восстановить ответ.

В каждой задаче свой способ восстановления ответа, но самые распространенные:

Небольшие оптимизации

Память

Зачастую в динамике можно встретить задачу, в которой состояние требует быть посчитанными не очень большое количество других состояний. Например, при подсчёте чисел Фибоначчи мы используем только два последних, а к предыдущим уже никогда не обратимся. Значит, можно про них забыть, то есть не хранить в памяти. Иногда это улучшает асимптотическую оценку по памяти. Этим приёмом можно воспользоваться в примерах №1, №2, №3 (в решении без матрицы перехода), №7 и №8. Правда, этим никак не получится воспользоваться, если порядок обхода — ленивая динамика.

Время

Иногда бывает так, что можно улучшить асимптотическое время, используя какую-нибудь структуру данных. К примеру, в алгоритме Дейкстры можно воспользоваться очередью с приоритетами для изменения асимптотического времени.

Замена состояния

В решениях динамикой обязательно фигурирует состояние — параметры, однозначно задающие подзадачу, но это состояние не обязательно одно единственное. Иногда можно придумать другие параметры и получить с этого выгоду в виде снижения асимптотического времени или памяти.

Пример №9: Разложение числа

Решение №1:

Решение №2:

Строки здесь обозначают слагаемые.

Первое решение последовательно добавляет по одной строчке внизу таблицы, а второе — по одному столбцу слева таблицы. Вариантов размера следующей строчки много — главное, чтобы она была больше предыдущей, а столбцов — только два: такой же как предыдущий и на единичку больше.

Заключение

Основным источником была голова, а туда информация попала с лекций в Летней Компьютерной Школе (для школьников), а также кружка Андрея Станкевича и спецкурса Михаила Дворкина (darnley).

Спасибо за внимание, надеюсь эта статья кому-нибудь пригодится! Хотя мне уже пригодилась — оказывается, написание статьи это хороший способ всё вспомнить.

Источник

Вопросы с ответами по дисциплине «математические методы в экономике»

1. Что является объектом и языком исследования в экономико-математическом моделировании:

A) различные типы производственного оборудования и методы его конструирования;

B) экономические процессы и специальные математические методы;

C) компьютерные программы и языки программирования.

2. Какое матричное уравнение описывает замкнутую экономическую модель Леонтьева:

3. Какое допущение постулируется в модели Леонтьева многоотраслевой экономики:

A) выпуклость множества допустимых решений;

B) нелинейность существующих технологий;

C) линейность существующих технологий.

4. Какое уравнение называется характеристическим уравнением матрицы А:

5. Множество n – мерного арифметического точечного пространства называется выпуклым, если:

A) вместе с любыми двумя точками А и В оно содержит и весь отрезок АВ;

B) счетно и замкнуто;

C) равно объединению нескольких конечных множеств.

6. Какая задача является задачей линейного программирования:

A) управления запасами;

B) составление диеты;

C) формирование календарного плана реализации проекта.

7. Задача линейного программирования называется канонической, если система ограничений включает в себя:

A) только неравенства;

B) равенства и неравенства;

C) только равенства.

8. Тривиальными ограничениями задачи линейного программирования называются условия:

A) ограниченности и монотонности целевой функции;

B) не отрицательности всех переменных;

C) не пустоты допустимого множества.

9. Если в задаче линейного программирования допустимое множество не пусто и целевая функция ограничена, то:

A) допустимое множество не ограничено;

B) оптимальное решение не существует;

C) существует хотя бы одно оптимальное решение.

10. Симплекс-метод предназначен для решения задачи линейного программирования:

A) в стандартном виде;

B) в каноническом виде;

C) в тривиальном виде.

11. Неизвестные в допустимом виде системы ограничений задачи линейного программирования, которые выражены через остальные неизвестные, называются:

12. Правильным отсечением в задаче целочисленного программирования называется дополнительное ограничение, обладающее свойством:

A) оно должно быть линейным;

B) оно должно отсекать хотя бы одно целочисленное решение;

C) оно не должно отсекать найденный оптимальный нецелочисленный план.

13. Какой из методов целочисленного программирования является комбинированным:

C) метод ветвей и границ.

14. Какую особенность имеет динамическое программирование как многошаговый метод оптимизации управления:

A) отсутствие последействия;

B) наличие обратной связи;

C) управление зависит от бесконечного числа переменных.

15. Вычислительная схема метода динамического программирования:

A) зависит от способов задания функций;

B) зависит от способов задания ограничений;

C) связана с принципом оптимальности Беллмана.

16. Какую задачу можно решить методом динамического программирования:

A) транспортную задачу;

B) задачу о замене оборудования;

C) принятия решения в конфликтной ситуации.

17. Метод скорейшего спуска является:

A) методом множителей Лагранжа;

B) градиентным методом;

C) методом кусочно-линейной аппроксимации.

18. Множители Лагранжа в экономическом смысле характеризуют:

A) доход, соответствующий плану;

B) издержки ресурсов;

C) цену (оценку) ресурсов.

19. Функция нескольких переменных называется сепарабельной, если она может быть представлена в виде:

A) суммы функций одной переменной;

B) произведения функций нескольких переменных;

C) суммы выпуклых функций.

20. Платежной матрицей называется матрица, элементами которой являются:

A) годовые прибыли отраслевых предприятий;

B) выигрыши, соответствующие стратегиям игроков;

C) налоговые платежи предприятий.

21. Верхней ценой парной игры является:

A) гарантированный выигрыш игрока А при любой стратегии игрока В;

B) гарантированный выигрыш игрока В;

C) гарантированный проигрыш игрока В.

22. Чистой ценой игры называется:

A) верхняя цена игры;

B) нижняя цена игры;

C) общее значение верхней и нижней ценой игры.

23. Возможно ли привести матричную игру к задаче линейного программирования:

C) возможно, если платежная матрица единичная.

24. Кооперативные игры – это игры:

A) с нулевой суммой;

B) со смешанными стратегиями;

C) допускающие договоренности игроков.

25. Какие математические методы можно применять для принятия хозяйственных решений в условиях неопределенности:

A) линейного программирования;

B) массового обслуживания;

C) динамического программирования.

26. Главными элементами сетевой модели являются:

A) игровые ситуации и стратегии;

B) состояния и допустимые управления;

C) события и работы.

27. В сетевой модели не должно быть:

A) контуров и петель;

B) собственных векторов;

28. Критическим путем в сетевом графике называется:

A) самый короткий путь;

B) самый длинный путь;

29. Математической основой методов сетевого планирования является:

A) аналитическая геометрия;

B) теория электрических цепей;

30. Какая из данных экономико-математичеких моделей является однофакторной:

A) модель материализованного технического прогресса;

Источник

Динамическое программирование

Динамическое программирование — это метод оптимизации, приспособленный к операциям, в которых процесс принятия решения может быть разбит на этапы (шаги). Такие операции называются многошаговыми. Начало развития динамического программирования относится к 50-м гг. прошлого века и связано с именем Р. Веллмана.

Ричард Беллман (26 августа 1920, Нью-Йорк — 19 марта 1984, Лос-Анджелес) — американский математик, один из основоположников динамического программирования, выдающийся специалист в области прикладной математики и вычислительной техники. Работал ассистентом математики в Принстонском университете (1946-1948), затем после защиты диссертации профессором мате

матики в Стэнфордском университете (1948-1952).Научный сотрудник RAND Corporation (1953-1965). С1965 г. и до своей кончины читал лекции в университете Южной Калифорнии. Получил многочисленные результаты, связанные с применением динамического программирования в разных областях математики (вариационное исчисление, автоматическое регулирование, теория аппроксимации, исследование операций и др.). В вариационном исчислении важную роль играет функциональное уравнение Веллмана. В математических методах оптимального управления известны функция Веллмана и уравнение Веллмана. Ричард Веллман опубликовал 619 статей и 39 книг. Многие его работы переведены на русский язык.

Если модели линейного программирования можно использовать для принятия крупномасштабных плановых решений в сложных ситуациях, то модели динамического программирования (ДП) применяются при решении задач значительно меньшего масштаба, например при разработке правил управления запасами, устанавливающего момент пополнения запасов и размер пополняющего заказа; при разработке принципов календарного планирования производства и выравнивания занятости в условиях колеблющегося спроса на продукцию; при распределении дефицитных капитальных вложений между возможными новыми направлениями их использования; при составлении календарных планов текущего и капитального ремонта сложного оборудования и его замены; при разработке долгосрочных правил замены выбывающих из эксплуатации основных фондов и т. п.

В реально функционирующих больших экономических системах еженедельно требуется принимать микроэкономические решения. Модели ДП ценны тем, что позволяют на основе стандартного подхода при минимальном вмешательстве человека принимать такие решения. И если каждое взятое в отдельности такое решение малосущественно, то в совокупности эти решения могут оказать большое влияние на прибыль.

Приведем общую постановку задачи ДП. Рассматривается управляемый процесс, например экономический процесс распределения средств между предприятиями, использования ресурсов в течение ряда лет, замены оборудования, пополнения запасов и т. п. В результате управления система (объект управления) 5 переводится из начального состояния s₀ в состояние s. Предположим, что управление можно разбить на п шагов, т. е. решение принимается последовательно на каждом шаге, а управление, переводящее систему S из начального состояния в конечное, представляет собой совокупность п пошаговых управлений.

из состояния s₀ в состояние s. Обозначим через s_k состояние системы после к-го шага управления. Получаем последовательность состояний s₀,s_]. s_k__],s_k. s_n__vs_n = s, которую изобразим кружками (рис. 3.2.1).

Рис. 3.2.1. Последовательность состояний системы при воздействии управления

Показатель эффективности рассматриваемой управляемой операции — целевая функция — зависит от начального состояния и управления:

Сделаем несколько предположений.

1. Состояние s_k системы в конце к-го шага зависит только от предшествующего состояния s_k__] и управления на к-м шаге X _к (и не зависит от предшествующих состояний и управлений). Это требование называется «отсутствием последствия». Сформулированное положение записывается в виде уравнений

которые называются уравнениями состояний.

2. Целевая функция (3.2.1) является аддитивной от показателя эффективности каждого шага. Обозначим показатель эффективности к-го шага через

Задача пошаговой оптимизации (задача ДП) формулируется так: определить такое допустимое управление X, переводящее систему S из состояния s₍₎ в состояние s, при котором целевая функция (3.2.4) принимает наибольшее (наименьшее) значение.

Выделим особенности модели ДП:

Следует помнить, что существуют различные способы решения подобных задач, применяемые в зависимости от вида функций, ограничений, размерности и т. п. Рассмотрим вычислительную схему ДП, которая окажется безразличной к способам задания функций и ограничений. Вычислительная схема связана с принципом оптимальности и использует рекуррентные соотношения.

Принцип оптимальности впервые был сформулирован Веллманом в 1953 г. Его формулировка такова: «Каково бы ни было состояние s системы в результате какого-либо числа шагов, на ближайшем шаге нужно выбирать управление так, чтобы оно в совокупности с оптимальным управлением на всех последующих шагах приводило к оптимальному выигрышу на всех оставшихся шагах, включая данный». Веллманом были четко сформулированы и условия, при которых принцип верен. Основное требование — процесс управления должен быть без обратной связи, т. е. управление на данном шаге не должно оказывать влияния на предшествующие шаги.

Принцип оптимальности утверждает, что для любого процесса без обратной связи оптимальное уравнение таково, что оно является оптимальным для любого подпроцесса по отношению к исходному состоянию этого подпроцесса. Поэтому решение на каждом шаге оказывается наилучшим с точки зрения управления в целом. Если изобразить геометрически оптимальную траекторию в виде ломаной линии, то любая часть этой ломаной будет являться оптимальной траекторией относительно начала и конца.

Источник