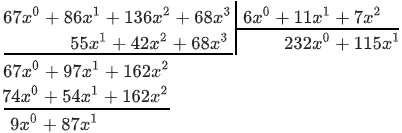как построить поле галуа

Инструменты сайта

Основное

Навигация

Информация

Действия

Содержание

Поля Галуа

Структура конечного поля

Существование конечных полей, т.е. полей, состоящих из конечного числа элементов установлено в пункте ☞ ПОЛЕ.

Нет ли противоречий в этих построенных таблицах?

В самом деле, возможно, что существует не найденная нами цепочка действий, которая приведет к противоречию с каким-то результатом из полученных таблиц. Ответ на этот вопрос оказывается отрицательным: противоречий мы не получим.

Пример. Рассмотрим множество, состоящее из квадратных матрицы второго порядка

Обобщенная теорема Ферма

Пример конечного поля

Ответ. Нет.

Подсказка: см. доказательство теоремы ☞ ЗДЕСЬ.

Пример. Для

Теорема. Конечные поля одинакового порядка изоморфны, т.е. между элементами этих полей можно установить такое взаимно-однозначное соответствие, которое сохраняет результаты сложения и умножения элементов.

Доказательства этой теоремы, приведенные в литературе, оказались трудны для моего понимания, поэтому я просто привожу проверку этого утверждения на примере ☞ ЗДЕСЬ.

Полиномы, неприводимые по модулю

В настоящем пункте под неприводимым полиномом понимается нормализованный неприводимый полином.

Непосредственным следствием теоремы 2 является

Доказательство (и критерий, часто позволяющий быстро отыскать такие корни) ☞ ЗДЕСЬ.

Полиномы над GF(2)

Заметим, что любой (не тождественно нулевой) полином из такого поля всегда нормализован.

Вывод. Поле Галуа одновременно обладает свойствами циклической группы, линейного пространства и алгебраического уравнения с целыми коэффициентами. С одной стороны, все ненулевые элементы поля можно представить как степени одного единственного. С другой стороны, операция сложения полиномов эквивалентна сложению векторов, составленных из их коэффициентов. Заметим, что в линейном пространстве не вводится аналога умножения векторов — такого, чтобы при умножении двух векторов получался снова вектор. С третьей стороны, все элементы поля разбиваются на подмножества, каждому из которых соответствует неприводимое алгебраическое уравнение — говорят, что элементы поля являются корнями неприводимых над GF(2) полиномов.

Решение ☞ ЗДЕСЬ.

Решение ☞ ЗДЕСЬ.

Полиномы над GF(p)

Источники

[1]. Чеботарев Н. Основы теории Галуа. Часть I. М.-Л.ОНТИ. 1934.

[2]. Питерсон У., Уэлдон Э. Коды, исправляющие ошибки. М.Мир. 1976.

[3]. Лидл Р., Нидеррайтер Г. Конечные поля. Том 1. М.Мир. 1988.

[4]. Ротман Т. Короткая жизнь Эвариста Галуа. Scientific American. N 1, 1983, cc. 84-93. Текст ☞ ЗДЕСЬ.

Источник

Арифметика полей Галуа для кодирования информации кодами Рида-Соломона

Коды Рида-Соломона относятся к недвоичным, блочным, помехоустойчивым кодам и могут использоваться в области хранения информации для избегания потери поврежденной информации.

На хабре есть пост посвященный кодированию информации кодами Рида-Соломона, но для примера автор использует простое поле Галуа. В данной статье описывается работа с расширенными полями Галуа, в частности GF(2^m), которые рационально использовать для цифровой информации. С моей аналогичной реализацией кодирования, декодирования, исправления ошибки можно ознакомится здесь.

При работе с кодами Рида-Соломона процент избыточных символов в 2 раза больше восстанавливаемого объема данных. Объясню на примере: если мы имеем последовательность из 10 символов и хотим иметь возможность восстановить ошибки в 3-ех из них (30% исходной информации), то нам нужно хранить 10+3*2=16 символов. Назовем каждую переменную: n = 10, количество информационных символов; f = 3, количество восстанавливаемых символов; g = 16, длина закодированной последовательности. Таким образом, формулу можно записать так: g = n + f * 2.

Поля Галуа

Для работы с информацией при кодировании и декодировании данных все арифметические операции выполняются в полях Галуа. Применяется так называемая полиномиальная арифметика или арифметика полей Галуа. Таким образом, результат любой операции также является элементом данного поля. Конкретное поле Галуа состоит из фиксированного диапазона чисел. Характеристикой поля называют некоторое простое число p. Порядок поля, т.е. количество его элементов, является некоторой натуральной степенью характеристики pm, где m∈N. При m=1 поле называется простым. В случаях, когда m>1, для образования поля необходим еще порождающий полином степени m, такое поле называется расширенным. GF(p^m) – обозначение поля Галуа.

Для работы с цифровыми данными естественно использовать p=2 в качестве характеристики поля. При m=1 элементом кодовой последовательности будет бит, при m=8 – 8 бит, то есть байт. Собственно коды Рида-Соломона работающие с байтами и являются наиболее распространенными.

Перед тем как переходить к операциям кодирования и декодирования разберемся с арифметикой полей Галуа на примере GF(2^3). Данное поле состоит из чисел от 0 до 7.

Операция сложения

Самой простой является операция сложения, которая является простым побитовым сложение по модулю 2 (ХОR).

Операция умножения

К сожалению, операция умножения гораздо сложнее, чтобы ее осуществить, необходимо преобразовать числа в полиномиальную форму.

Как можно заметить число в полиномиальной форме представляет собой многочлен, коэффициентами которого являются значения разрядов в двоичном представлении числа.

Перемножим два числа в полиномиальной форме:
5∙7=(x^2+1)∙(x^2+x+1)=x^4+x^3+x^2+x^2+x+1=x^4+x^3+x+1=11011=27

Итак, во-первых, следует заметить, что даже в полиномиальной форме осуществляется сложение по модулю 2, поэтому x^2+x^2=0. Во-вторых, результат умножения 27 не входит в используемое поле GF(2^3) (оно же состоит из чисел от 0 до 7, как было сказано выше). Чтобы бороться с этой проблемой, необходимо использовать порождающий полином. Порождающий полином является неприводимым, то есть простым (по аналогии с простыми числами делится без остатка на 1 и на самого себя). В арифметике полей Галуа неприводимым полиномом является аналог простых чисел. Используем для примера порождающий полином f(x)=x^3+x+1.

Также предполагается, что x удовлетворяет уравнению f(x)=x^3+x+1=0

Вернемся к примеру с умножением:

Составим таблицу умножения:

Операция деления

Операцию деления в полиномиальной форме понять, возможно, но достаточно тяжело. Поэтому гораздо лучше осуществлять его по таблице умножения.

Большое значение имеет таблица степеней элементов поля Галуа. Возведение в степень также осуществляется в полиномиальной форме, аналогично умножению.

Таким образом, составим таблицу степеней:

Таблица степеней обладает цикличностью: седьмая степень соответствует нулевой, значит восьмая соответствует первой и т.д. При желании можно это проверить.

В полях Галуа существует понятие примитивного члена – элемент поля, чьи степени содержать все ненулевые элементы поля. Просмотрев таблицу степеней видно, что этому условию соответствуют все элементы (ну кроме 1 естественно). Однако это выполняется не всегда, для примера приведу таблицу степеней для GF(16).

Для полей, которые мы рассматриваем, то есть с характеристикой 2, в качестве примитивного члена всегда выбирают 2. Учитывая его свойство, любой элемент поля можно выразить через степень примитивного члена.
Пример: 5=26, 7=25

Воспользовавшись этим свойством, и учитывая цикличность таблицы степеней, попробуем снова перемножить числа:
5∙7=2^6∙2^5=2^(6+5)=2^11=2^(11 mod 7)=2^4=6
Результат совпал с тем, что мы вычислили раньше.

А теперь выполним деление:
6÷5=2^4÷2^6=2^(4-6)=2^(-2)=2^((-2)mod 7)=2^5=7
Полученный результат тоже соответствует действительности.

Ну и для полноты картины посмотрим на возведение в степень:
5^2=(〖2^6)〗^2=2^(6∙2)=2^12=2^(12 mod 7)=2^5=7
Опять неожиданно получился такой же результат.

Такой подход к умножению и делению гораздо проще, чем реальные операции с использование полиномов, и для них нет необходимости хранить большую таблицу умножения, а достаточно лишь строки степеней примитивного члена поля.

Источник

Поле Галуа на Scala

Введение

В этой статье будет рассмотрена тема построения и работы с конечными полями (или полями Галуа), которые используются в криптографии, теории информации и кодирования и других науках, т.е. имеют широкое практическое применение. Сухую теорию о группах/кольцах/полях можно прочитать по ссылке Поля Галуа, а здесь будет больше практики и реализации на языке Scala.

Типы и ограничения

Для начала следует обсудить технические проблемы связанные с представлением полиномов в памяти, с учетом размеров типа Int в языке Scala. Требования сформулированы в списке ниже.

Реализация

Сначала опишем класс Polynomial, который реализует полином и 4 операции. Этот вид полинома является «полуфабрикатом» и не привязан к конечному полю.

Далее абстрактный класс FiniteField, который будет родителем полей Галуа. Внутри FiniteField содержится внутренний класс FiniteFieldPolynomial, такая структура позволяет обеспечить безопасность при проведении операций.

Безопасность заключается в том, что операции возможно производить только с полиномами из одного поля.

Обратите внимание на член modulo, это модуль (или же неприводимый полином) степени поля.

Важным этапом построения поля Галуа есть вычисление неприводимых полиномов степени поля, а так же выбор одного из них. С математикой данного процесса можно ознакомиться по ссылке Неприводимые полиномы.

Неприводимый полином будет использоваться для операций умножения и деления, точно так же как простое число для числового поля .

Иными словами, неприводимыые полиномы играют ту же роль во множествах полиномов, что и простые числа во множествах целых чисел.

Упрощенный код для нахождения множества неприводимых полиномов представлен ниже. Алгоритм следующий:

Осталось реализовать конкретный класс-наследник FiniteField, который будет готовым конечным полем.

Результат умножения может «вылезти» за рамки поля, поэтому иногда надо делить результат на модуль поля. Заметьте как реализовано деление, оно есть умножение a на мультипликативную инверсию b.

В свою очередь инверсия находится с помощью деления, определенного в классе Polynomial.

Вывод

Получилась самодельная реализация полей Галуа, которая в дальнейшем может быть улучшена путем увеличения возможного размера поля (вместо Int использовать длинную арифметику или что то в этом роде).

Данная статья может быть полезен студентам и всем кому интересна тема абстрактной алгебры, полей и теории кодирования.

Полный код приложения можно найти на github’е.

Источник

Инструменты сайта

Основное

Навигация

Информация

Действия

Содержание

Поле Галуа GF(16) (версия для программистов)

Умножение

Пример. Пусть

Деление

Возведение в степень

$$ \begin \mathfrak A^0 & & & & \mathfrak e & 0001 & & \\ \mathfrak A^1 & & & \mathfrak A & & 0010 & \Pi & f=0 \\ \mathfrak A^2 & & \mathfrak A^2 & & & 0100 & \Pi & f=0 \\ \mathfrak A^3 & \mathfrak A^3 & & & & 1000 & & f_3=0 \\ \hline \mathfrak A^4 & & & \mathfrak A & +\mathfrak e & 0011 & \Pi & f=0 \\ \mathfrak A^5 & & \mathfrak A^2 & +\mathfrak A & & 0110 & & f_4=0 \\ \mathfrak A^6 & \mathfrak A^3 & +\mathfrak A^2 & & & 1100 & & f_3=0\\ \mathfrak A^7 & \mathfrak A^3 & & + \mathfrak A & +\mathfrak e & 1011 & \Pi & f^<\ast>=0 \\ \hline \mathfrak A^8 & & \mathfrak A^2 & & +\mathfrak e & 0101 & \Pi & f=0 \\ \mathfrak A^9 & \mathfrak A^3 & & +\mathfrak A & & 1010 & & f_3=0 \\ \mathfrak A^ <10>& & \mathfrak A^2 &+\mathfrak A & +\mathfrak e & 0111 & & f_4=0 \\ \mathfrak A^ <11>& \mathfrak A^3 & +\mathfrak A^2 & +\mathfrak A & & 1110 & \Pi & f^<\ast>=0 \\ \hline \mathfrak A^ <12>& \mathfrak A^3 & +\mathfrak A^2 & + \mathfrak A& +\mathfrak e & 1111 & & f_3=0 \\ \mathfrak A^ <13>& \mathfrak A^3 & +\mathfrak A^2 & & +\mathfrak e & 1101 & \Pi & f^<\ast>=0 \\ \mathfrak A^ <14>& \mathfrak A^3 & & & +\mathfrak e & 1001 & \Pi & f^<\ast>=0 \end $$ Обоснование таблицы ☞ ЗДЕСЬ.

Поскольку это поле часто использую для иллюстраций, приведу еще одну таблицу — для степенных представлений элементов:

$$ \begin & \mathfrak A^0 & \mathfrak A^1 & \mathfrak A^2 & \mathfrak A^3 & \mathfrak A^4 & \mathfrak A^5 & \mathfrak A^6 & \mathfrak A^7 & \mathfrak A^8 & \mathfrak A^9 & \mathfrak A^ <10>& \mathfrak A^ <11>& \mathfrak A^ <12>& \mathfrak A^ <13>& \mathfrak A^ <14>\\ \hline \hline \mathfrak A^0 & \mathfrak o & \mathfrak A^4 & \mathfrak A^8 & \mathfrak A^ <14>& \mathfrak A & \mathfrak A^ <10>& \mathfrak A^ <13>& \mathfrak A^ <9>& \mathfrak A^ <2>& \mathfrak A^ <7>& \mathfrak A^ <5>& \mathfrak A^ <12>& \mathfrak A^ <11>& \mathfrak A^ <6>& \mathfrak A^ <3>\\ \hline \mathfrak A^1 & & \mathfrak o & \mathfrak A^5 & \mathfrak A^9 & \mathfrak A^0 & \mathfrak A^2 & \mathfrak A^ <11>& \mathfrak A^ <14>& \mathfrak A^ <10>& \mathfrak A^ <3>& \mathfrak A^ <8>& \mathfrak A^ <6>& \mathfrak A^ <13>& \mathfrak A^ <12>& \mathfrak A^ <7>\\ \hline \mathfrak A^2 & & & \mathfrak o & \mathfrak A^ <6>& \mathfrak A^ <10>& \mathfrak A^ <1>& \mathfrak A^ <3>& \mathfrak A^ <12>& \mathfrak A^0 & \mathfrak A^ <11>& \mathfrak A^ <4>& \mathfrak A^ <9>& \mathfrak A^ <7>& \mathfrak A^ <14>& \mathfrak A^ <13>\\ \hline \mathfrak A^3 & & & & \mathfrak o & \mathfrak A^ <7>& \mathfrak A^ <11>& \mathfrak A^ <2>& \mathfrak A^ <4>& \mathfrak A^ <13>& \mathfrak A^ <1>& \mathfrak A^ <12>& \mathfrak A^ <5>& \mathfrak A^ <10>& \mathfrak A^ <8>& \mathfrak A^0 \\ \hline \mathfrak A^4 & & & & & \mathfrak o & \mathfrak A^8 & \mathfrak A^ <12>& \mathfrak A^3 & \mathfrak A^5 & \mathfrak A^ <14>& \mathfrak A^2 & \mathfrak A^ <13>& \mathfrak A^6 & \mathfrak A^ <11>& \mathfrak A^9 \\ \hline \mathfrak A^5 & & & & & & \mathfrak o & \mathfrak A^9 & \mathfrak A^ <13>& \mathfrak A^4 & \mathfrak A^6 & \mathfrak A^0 & \mathfrak A^3 & \mathfrak A^ <14>& \mathfrak A^7 & \mathfrak A^ <12>\\ \hline \mathfrak A^6 & & & & & & & \mathfrak o & \mathfrak A^ <10>& \mathfrak A^ <14>& \mathfrak A^ <5>& \mathfrak A^ <7>& \mathfrak A & \mathfrak A^ <4>& \mathfrak A^ <0>& \mathfrak A^ <8>\\ \hline \mathfrak A^7 & & & & & & & & \mathfrak o & \mathfrak A^ <11>& \mathfrak A^0 & \mathfrak A^ <6>& \mathfrak A^ <8>& \mathfrak A^2 & \mathfrak A^ <5>& \mathfrak A \\ \hline \mathfrak A^8 & & & & & & & & & \mathfrak o & \mathfrak A^ <12>& \mathfrak A & \mathfrak A^ <7>& \mathfrak A^ <9>& \mathfrak A^ <3>& \mathfrak A^ <6>\\ \hline \mathfrak A^9 & & & & & & & & & & \mathfrak o & \mathfrak A^ <13>& \mathfrak A^ <2>& \mathfrak A^ <8>& \mathfrak A^ <10>& \mathfrak A^ <4>\\ \hline \mathfrak A^ <10>& & & & & & & & & & & \mathfrak o & \mathfrak A^ <14>& \mathfrak A^ <3>& \mathfrak A^ <9>& \mathfrak A^ <11>\\ \hline \mathfrak A^ <11>& & & & & & & & & & & & \mathfrak o & \mathfrak A^0 & \mathfrak A^ <4>& \mathfrak A^ <10>\\ \hline \mathfrak A^ <12>& & & & & & & & & & & & & \mathfrak o & \mathfrak A^ <1>& \mathfrak A^ <5>\\ \hline \mathfrak A^ <13>& & & & & & & & & & & & & & \mathfrak o & \mathfrak A^ <2>\\ \hline \mathfrak A^ <14>& & & & & & & & & & & & & & & \mathfrak o \end $$ ♦

Вопрос для тех, кто у меня учился: вам ничего этот алгоритм не напоминает?

Уравнения линейные

Пример. Решить систему уравнений

В поле предыдущего примера решить системы уравнений

А уж если ввели определитель, то самое время ввести понятие матрицы из элементов поля — хотя бы для того, чтобы иметь возможность выписать решение системы л.у. с помощью обратной матрицы. Но пока повременим с развитием этой идеи, а попробуем взглянуть на решение предыдущего примера альтернативным взглядом.

Матрицы

Пример.

Подводя итог: в дополнение к упомянутым ☝ ВЫШЕ интерпретациям поля Галуа, добавим еще одно. Ненулевой элемент поля Галуа — это

Восстановление утерянной информации

Собранного в предыдущих пунктах алгебраического формализма достаточно, чтобы попытаться объяснить «на пальцах» его применения для решения задач помехоустойчивого кодирования.

Для решения этой задачи нужны ресурсы. И этими ресурсами являются, во-первых, дополнительные — служебные — разряды, которые подсоединяются к информационным разрядам (и, следовательно, тоже участвуют в процессе коммуникации), и, во-вторых, имеющиеся в нашем распоряжении вычислительные мощности, позволяющие наполнять содержимое служебных разрядов — в зависимости от содержимого разрядов информационных, а также выполнять собственно задачу восстановления утраченного.

Места потерь известны

Пример. Пусть

Места потерь неизвестны

Обратимся теперь к решению более сложной задачи: когда в процессе коммуникации портится содержимое одного или нескольких информационных блоков, но номера этих блоков нам неизвестны.

Пример. Пусть на выходе канала связи получена информационная строка, разбиение которой на блоки имеет вид:

Пример. Пусть на выходе канала связи получена информационная строка, разбиение которой на блоки имеет вид:

Уравнения нелинейные

Основываясь на этих (весьма неполных) экспериментальных данных, сделаем общие выводы:

Источник

Арифметика с полиномами для кода Рида-Соломона

Если хочется сделать передачу или хранение данных более надёжными, применив к ним избыточное кодирование, то для этого неплохо подойдёт код Рида-Соломона. Понимаю, что на эту тему написано немало материала, тем не менее ориентирован он, как правило, на людей неплохо подготовленных в математике. Если просто хочется реализовать такой алгоритм в каком-нибудь проекте, не сильно углубляясь в математику, то надеюсь этот материал будет весьма полезным.

При кодировании Рида-Соломона сообщения представляются в виде полиномов, дальше с этими полиномами выполняются разные арифметические операции. Но прежде чем приступать к операциям над полиномами нужно вспомнить (узнать) об полях Галуа.

Арифметика в поле Галуа GF[256]

В своей предыдущей, первой во всех смыслах статье, я подробно описал, как можно реализовать умножение в полях Галуа и приводил пример кода на C#. Там же я кратко писал что такое поля Галуа и зачем они нужны.

Напомню. В нашей привычной арифметике результатом операции деления может оказаться дробное число вроде (1/3). В десятичном представлении это 0,3333333… и так далее. Такие числа не очень удобны для компьютерных вычислений, так что для кодирования информации решили применить давно придуманные поля Галуа. Здесь числа это такие же привычные нам числа, только их количество – это строго определённая величина. Для кодирования хорошо подходит поле GF[256] (Galois Field 256 – поле Галуа, содержащее 256 элементов), То есть вместо всех привычных значений от до , с вообще всеми возможными промежуточными, включая , , 42, а также гугол и прочие, у нас есть 256 чисел: 0, 1, 2… 255. Всё. Никаких тебе 7092, 3,15 и 2/3. Только числа из списка. (42 — в списке. Без паники).

Но просто так числа ничего не дают. Вся их польза – это операции. Их можно складывать, вычитать, делить и умножать, только это не просто так сложил-вычел. Результат сложения-вычитания-деления-умножения есть число также от 0 до 255. Какое это число? Два плюс два равно сколько? Так вот, ни разу не 4. 2+2=0. Вообще, сложение в GF[256] работает также, как и вычитание. это побитовое исключающее «или» – XOR. Умножение-деление — там другие правила, но на простейшем уровне можно считать, что это таблицы. Так как чисел ограниченное количество, то можно составить всеобъемлющую таблицу умножения. Каким образом? Совсем детально здесь не буду распространяться. Про умножение – подробно писал в предыдущей статье, деление и возведение в степень проще всего реализовать используя таблицы степеней и логарифмов. Да, умножение тоже можно реализовать с помощью логарифмов, так эта операция выполняется быстрее.

Ну конечно же, кодирование и декодирование будут делать не специально обученные эмигранты с калькуляторами. Это должно быть реализовано программно. Конечно же это должен быть язык низкого уровня, какой кому ближе. Может быть, даже verilog (в этом случае речь идёт уже об аппаратной реализации, и на самом деле, как заметили в комментариях, verilog относится к языкам высокого уровня). Для того чтобы разобраться как работает кодирование, для себя я решил написать все алгоритмы на высокоуровневом C#, но постарался не сильно задействовать высокий уровень абстракции. Просто чтобы разобраться. Должен сразу сказать, что мой код ни коим образом не претендует ни на быстродействие, ни на оптимальность или на правильность с точки зрения ООП либо каких-нибудь ещё паттернов или подходов. Единственно, я старался, чтобы код был максимально понятным. Весь код вместе с каким-никаким GUI выложен на гитхабе. Собирается под win в VS2019. Бинарник тоже выложен.

Для начала нужно составить таблицы степеней и логарифмов примитивного члена. Здесь надо напомнить (рассказать) про свойство возведения в степень в поле Галуа. Если последовательно умножать (по правилам поля, конечно) двойку: , то начиная со степени 255 результат начнёт повторяться, то есть и также . Если упорно продолжить умножать дальше, пока есть терпение и деньги на зарплату эмигрантам, то результат будет такой:

и так далее. Значения, если использовать порождающий полином 285 (о нём было в предыдущей статье сейчас это не сильно важно), такие:

Также в промежутке от до включительно нет ни одного повторяющегося результата. А это значит, что любое число (кроме нуля) из поля GF[256] можно записать как два в какой-нибудь степени. И что из этого? А вот что. Правила умножения и деления степеней здесь выполняются. То есть
а также . Это вместе значит, что не надо заморачиваться и реализовывать алгоритмы умножения и деления по сложным правилам, достаточно лишь узнать в какой степени двойка для каждого множителя (логарифм) и сложить или вычесть степени чтобы произвести операции умножения или деления. Пример:

Возведение в степень и нахождение логарифма – просто обращение к массивам, в которых по 256 элементов (так как , для таблицы степеней достаточно 255 элементов).

Теперь нужно сделать пару важных оговорок для тех, кто захочет самостоятельно реализовать алгоритмы исходя из описания. (Когда я изучал вопрос, везде эти вещи считались «очевидными» со всеми вытекающими)

И так, мы построили свою арифметику. С целыми числами и делением без остатка. Для простоты использования чисел GF[256] можно создать класс и в нём переопределить операции сложения, вычитания, деления и умножения. Так дальнейший код будет немного короче.

Полиномы

Переходим к полиномам. Для кодирования Рида-Соломона сообщения представляются в виде полиномов. Как правило, считается, что этой фразы достаточно. Но я распишу поподробнее, потому что, когда я изучал вопрос мне было не до конца всё понятно. Полином – это выражение вроде такого:

Член полинома – это или . Степень члена – это показатель , коэффициент члена это множитель перед x. Теперь, если мы хотим представить сообщение в виде полинома, то числовые значения байт сообщения мы записываем как коэффициенты членов. Ещё одна оговорка: при реализации умножения в поле Галуа (без таблиц степеней и логарифмов) также используются полиномы. Эти полиномы не имеют никакого отношения к тем, что мы рассматриваем здесь. Как говорится: «Это другое!»

Например нам нужно закодировать сообщение «DON’T PANIC». Для этого нужно перевести символы в числа. С русскими буквами было бы сложнее, там на каждый символ (UTF8) приходится по 2 байта. А здесь воспользуемся UTF8, или ASCII и получим: 44 4F 4E 27 54 20 50 41 4E 49 43 – это в шестнадцатеричном виде, или 68, 79, 78, 39, 84, 32, 80, 65, 78, 73, 67 обычными числами. Теперь записываем каждое число как коэффициент перед x, и получаем, что сообщению «DON’T PANIC» соответствует такой полином:

Степени можно расположить как в порядке возрастания, так и в порядке убывания. Полином в зависимости от этого остаётся полиномом, но становится другим полиномом и об этом надо помнить. То есть, выбор порядка нужно сделать один раз и его придерживаться. (В зависимости от этого выбора избыточные символы при кодировании будут находиться в начале или в конце сообщения). Для себя я выбрал возрастание степеней. Полином при этом выглядит задом наперёд (нулевая степень в начале, а не в конце, как принято в математике), но при этом номер члена равен его степени. Избыточные символы при кодировании будут в начале. При написании кода можно хранить лишь массив с коэффициентами, так что кодируемое сообщение это просто массив байт.

Операции с полиномами

Сложение и умножение полиномов (многочленов) – это, на самом деле, восьмой класс средней школы (точно не помню, может другой). Кому-то покажется излишним (мне точно кажется), но для полноты картины распишу с примерами. Для кодирования я выбрал записывать полиномы в порядке убывания степеней членов, так что и в примерах буду записывать также. Закодированное сообщение из примера выше в виде полинома довольно-таки громоздко, поэтому для примеров будут просто рандомные полиномы невысоких степеней.

Сложение полиномов

Для того чтобы сложить два полинома мы просто складываем коэффициенты при одинаковых степенях по правилам поля Галуа. Всё. Пример: выполняем следующую операцию:

Для программной реализации (и для кодирования) лучше записать полиномы так, чтобы они были одной длины и с явным указанием степеней:

В результате имеем:

Так как в поле GF[256] вычитание эквивалентно сложению то пишу только знак «+». Вычитание полиномов также эквивалентно сложению полиномов.

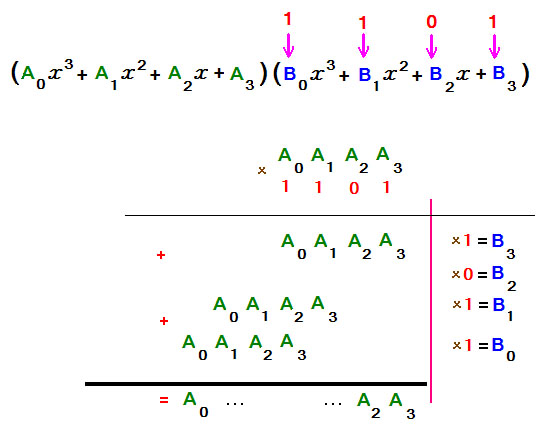
Умножение полиномов

При умножении каждый член одного полинома умножается на каждый член второго. Результат складывается:

Когда мы перемножаем и складываем коэффициенты — мы используем правила умножения и сложения поля Галуа GF[256]. Сложение степеней — это обычное сложение, то есть:

Деление полиномов

С делением всё немного сложнее, но тоже ничего сверхъестественного. Это как деление столбиком, только с полиномами. Берём старший член делимого и старший делителя. Делим, записываем результат. Полученное умножаем на делитель и вычитаем (прибавляем – в поле Галуа неважно) из делимого. Далее результат вычитания делим также, как делили изначально. Всё повторяется до тех пор, пока старшая степень остатка больше или равна старшей степени делителя.

Нужно разделить на . Записываем в столбик. Затем делим старшие члены: на (деление по правилам поля Галуа, вычитание степени — обычное). Результат записываем.

Теперь умножаем на . Получаем записываем это под делимым и складываем. Результат сложения также записываем под чертой (это остаток)

Теперь остаток также делим на делитель. (Делим старшие члены) умножаем — вычитаем — всё как на первом шаге:

В остатке теперь старший член – это . Степень меньше, чем у старшего члена делителя () – значит всё, деление закончено. Частное это , остаток .

Код деления умножения и вычитания хоть и не очень сложный, но довольно-таки громоздкий вместе со всеми вспомогательными функциями, без которых код не очень понятен. Думаю, здесь его приводить нет особого смысла. Но всё же продублирую ссылку на Github: https://github.com/AV-86/Reed-Solomon-Demo/releases

И какой толк от всех этих ваших полиномов? В принципе без алгоритмов кодирования-декодирования Рида-Соломона я не знаю как их с пользой применить. Слышал краем уха, что они также применяются при шифровании информации. Непосредственно как кодировать и декодировать по методу Рида-Соломона напишу в следующей статье, а пока, благодарю за внимание!

Источник