хорда окружности всегда больше чем радиус этой окружности

Что такое хорда окружности в геометрии, её определение и свойства

Хорда в переводе с греческого означает «струна». Это понятие широко применяется в разных областях науки — в математике, биологии и других.

В геометрии для термина определение будет следующим: это отрезок прямой линии, который соединяет между собой две произвольные точки на одной окружности. Если такой отрезок пересекает центр кривой, она называется диаметром описываемой окружности.

Как построить геометрическую хорду

Чтобы построить этот отрезок, прежде всего необходимо начертить круг. Обозначают две произвольные точки, через которые проводят секущую линию. Отрезок прямой, который располагается между точками пересечения с окружностью, называется хордой.

Если разделить такую ось пополам и из этой точки провести перпендикулярную прямую, она будет проходить через центр окружности. Можно провести обратное действие — из центра окружности провести радиус, перпендикулярный хорде. В этом случае радиус разделит её на две идентичные половины.

Если рассматривать части кривой, которые ограничиваются двумя параллельными равными отрезками, то эти кривые тоже будут равными между собой.

Свойства

Существует ряд закономерностей, связывающих между собой хорды и центр круга:

Взаимосвязь с радиусом и диаметром

Вышеуказанные математические понятия связаны между собой следующими закономерностями:

Хорда и радиус

Между этими понятиями существуют следующие связи:

Отношения со вписанными углами

Углы, вписанные в окружность, подчиняются следующим правилам:

Взаимодействия с дугой

Если два отрезка стягивают участки кривой, одинаковые по размеру, то такие оси равны между собой. Из этого правила вытекают следующие закономерности:

Хорда, которая стягивает ровно половину окружности, является её диаметром. Если две линии на одной окружности параллельны между собой, то будут равными и дуги, которые заключены между этими отрезками. Однако не следует путать заключённые дуги и стягиваемые теми же линиями.

Источник

Всё про окружность и круг

Кругом называется часть плоскости, ограниченная окружностью и включающая ее центр.

Отрезок, соединяющий две точки окружности, называется хордой. Хорда, проходящая через центр окружности, представляет собой диаметр. Диаметр окружности равен ее удвоенному радиусу: D = 2R.

Точка пересечения двух хорд делит каждую хорду на отрезки, произведение которых одинаково: a1a2 = b1b2

Касательная к окружности всегда перпендикулярна радиусу, проведенному в точку касания.

Отрезки касательных к окружности, проведенные из одной точки, равны: AB = AC, центр окружности лежит на биссектрисе угла BAC.

Квадрат касательной равен произведению секущей на ее внешнюю часть

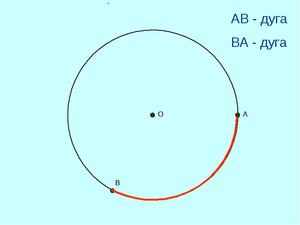
Дугой называется часть окружности, заключенная между двумя точками.

Мерой дуги (в градусах или радианах) является центральный угол, опирающийся на данную дугу.

Вписанный угол это угол, вершина которого лежит на окружности, а cтороны угла пересекают ее.

Вписанный угол равен половине центрального, если оба угла опираются на одну и ту же дугу окружности.
Внутренние углы, опирающиеся на одну и ту же дугу, равны.

Сектором круга называется геометрическая фигура, ограниченная двумя радиусами и дугой, на которую опираются данные радиусы.

Периметр сектора: P = s + 2R.

Площадь сектора: S = Rs/2 = ПR 2 а/360°.

Сегментом круга называется геометрическая фигура, ограниченная хордой и стягиваемой ею дугой.

Источник

Хорда окружности всегда больше чем радиус этой окружности

Ключевые слова: хорда, окружность, диаметр, круг

Окружностью называется фигура, состоящая из всех точек плоскости, находящихся от данной точки на данном расстоянии.
Данная точка называется центром окружности,
а отрезок, соединяющий центр с какой-либо точкой окружности, — радиусом окружности.
Часть плоскости, ограниченная окружностью называется кругом.

Круговым сектором или просто сектором называется часть круга, ограниченная дугой и двумя радиусами, соединяющими концы дуги с центром круга.
Сегментом называется часть круга, ограниченная дугой и стягивающей ее хордой.

Отрезок, соединяющий две точки окружности, называется ее хордой.
Хорда, проходящая через центр окружности, называется диаметром.

Свойства хорд

Диаметр (радиус), перпендикулярный к хорде, делит эту хорду и обе стягиваемые ею дуги пополам. Верна и обратная теорема: если диаметр (радиус) делит пополам хорду, то он перпендикулярен этой хорде.

Дуги, заключенные между параллельными хордами, равны. В окружности равные хорды равноудалены от центра окружности.

Если две хорды окружности, AB и CD пересекаются в точке M, то произведение отрезков одной хорды равно произведению отрезков другой хорды: AM•MB = CM•MD.

Источник

Хорда окружности — определение, свойства, теорема

Термин «хорда» используется в различных науках. Например, в биологии это означает скелетный гибкий стержень, в математике — отрезок, вписанный в окружность. В геометрии хорда окружности — это отрезок, который соединяет две точки окружности. Она является частью секущей, проведенной через окружность.

Хорда в геометрии

Каждая хорда имеет свою длину. Ее можно определить с помощью теоремы синусов. То есть длина хорды окружности зависит от радиуса и вписанного угла, опирающегося на данный отрезок. Формула для определения длины выглядит следующим образом: B*A = R*2 * sin α, где R — радиус, AB — это хорда, α — вписанный угол. Также длину можно вычислить через другую формулу, которая выводится из теоремы Пифагора: B*A = R*2 * sin α/2 , где AB — это хорда, α — центральный угол, который опирается на данный отрезок, R — радиус.

Если рассматривать хорды в совокупности с дугами, то получаются новые объекты. Например, в кругу можно дополнительно выделить две области: сектор и сегмент. Сектор образуется с помощью двух радиусов и дуги. Для сектора можно вычислить площадь, а если он является частью конуса, то еще и высоту. Сегмент, в свою очередь, это область, состоящая из отрезка и дуги.

Для того чтобы проверить правильность своего решения в нахождении длины, можно обратиться к онлайн-калькуляторам в интернете. Они представлены в виде таблицы, в которую нужно вписать только известные параметры, а программа сама выполнит необходимые вычисления.

Это очень полезная функция, так как не приходится вспоминать различные уравнения и производить сложные расчеты.

Свойства отрезка окружности

Для решения геометрических задач необходимо знать свойства хорды окружности. Для нее характерны такие показатели:

Помимо основных свойств отрезка круга, нужно выделить еще одно важное свойство. Оно отражено в теореме о пересекающихся хордах.

Ключевая теорема

Имеется круг с центром в точке O и радиусом R. Для теоремы нужно в круг вписать две прямые, пускай это будут хорды BA и CD, которые пересекаются в точке E. Перед тем как перейти к доказательству, нужно сформулировать определение теоремы. Оно звучит следующим образом: если хорды пересекаются в некоторой точке, которая делит их на отрезки, то произведения длин отрезков первой хорды равно произведению длин отрезков второй хорды. Для наглядности можно записать эту формулу: AE*BE= EC*ED. Теперь можно перейти к доказательству.

Проведем отрезки CB и AD. Рассмотрим треугольники CEB и DEA. Известно, что углы CEB и DEA равны как вертикальные углы, DCB и BAD равны за следствием с теоремы про вписанные углы, которые опираются на одну и ту же дугу. Треугольники CEB и DEA подобны (первый признак подобия треугольников). Тогда выходит пропорциональное соотношение BE/ED = EC/EA. Отсюда AE*BE= EC*ED.

Помимо взаимодействия с внутренними элементами окружности, для хорды еще существуют свойства при пересечении с секущейся и касательными прямыми. Для этого необходимо рассмотреть понятия касательная и секущая и определить главные закономерности.

Касательная — это прямая, которая соприкасается с кругом только в одной точке. И если к ней провести радиус круга, то они будут перпендикулярны. В свою очередь, секущая — это прямая, которая проходит через две точки круга. При взаимодействии этих прямых можно заметить некоторые закономерности.

Касательная и секущая

Существует теорема о двух касательных, которые проведены с одной точки. В ней говорится о том, что если есть две прямые OK и ON, которые проведены с точки O, будут равны между собой. Перейдем к доказательству теоремы.

Рассмотрим два прямоугольных треугольника AFD и AED. Поскольку катеты DF и DE будут равны как радиусы круга, а AD — общая гипотенуза, то между собой данные треугольники будут равны за признаком равенства треугольников, с чего выходит, что AF = AE.

Если возникает ситуация, когда пересекаются касательная и секущая, то в этом случае также можно вывести закономерность. Рассмотрим теорему и докажем, что AB 2 = AD*AC.

Предположим у нас есть касательная AB и секущая AD, которые берут начало с одной точки A. Обратим внимание на угол ABC, он спирается на дугу BC, значит, за свойством значение его угла будет равно половине градусной меры дуги, на которую он опирается. За свойством вписанного угла, величина угла BDC также будет равно половине дуги BC. Таким образом, треугольники ABD и ABC будут подобны за признаком подобия треугольников, так как угол A — общий, а угол ABC равен углу BDC. Опираясь на теорию, получаем соотношение: AB/CA = DA/AB, переписав это соотношение в правильную форму, получаем равенство AB 2 = AD*AC, что и требовалось доказать.

Как есть теорема про две касательные, так есть и теорема про две секущие. Она так же просто формулируется, как и остальные теоремы. Поэтому рассмотрим доказательство и убедимся, что AB*AC = AE*AD.

Проведем две прямые через точку A, получим две секущие AC и AE. Дорисуем две хорды, соединяя точки C и B, B и D. Получим два треугольника ABD И CEA. Обратим внимание на вписанный четырехугольник BDCE. За свойством вписанных четырехугольников узнаем, что значения углов BDE и ECB в сумме будут давать 180 градусов. И сумма значений углов BDA и BDE также равна 180, за свойством смежных углов.

Отсюда можно получить два уравнения, из которых будет выведено, что углы ECB и BDA будут равны: BDA + BDE = 180; BDE + ECB = 180. Все это записываем в систему уравнений, отнимаем первое от второго, получаем результат, что ECB = BDA.

Если вернутся к треугольникам ABD И CEA, то теперь можно сказать, что они подобны, так как угол А — общий, а углы ECA и BDA — равны. Теперь можно записать соотношение сторон: AB/AE = AD/AC. В итоге получим, что AB*AC = AE*AD.

Решение задач

При решении задач, связанных с окружностью, хорда часто выступает главным элементом, опираясь на который можно найти остальные неизвестные элементы. В каждой второй задаче задаются два параметра, чтобы найти третий неизвестный. В задачах, которые, связанные с кругом, хорда — это обязательный элемент:

Для решения задач с отрезком в окружности удобно использовать схематические рисунки. Их рисуют с помощью линейки и циркуля, и принцип решения задач становится более наглядным.

Источник

Хорда окружности всегда больше чем радиус этой окружности

Развернуть структуру обучения Свернуть структуру обучения Определение хорды Свойства хорды к окружности Свойства хорды и вписанного угла Свойства хорды и центрального угла Формулы нахождения хорды Длина хорды окружности равна удвоенному радиусу данной окружности, умноженному на синус половины центрального угла. Сумма квадрата половины длины хорды и квадрата перпендикуляра, проведенного к этой хорде, равна квадрату радиуса окружности. Данная формула следует из теоремы Пифагора. Решение задач Примечание. Если Вы не нашли решение подходящей задачи, пишите об этом в форуме. Наверняка, курс геометрии будет дополнен. Задача. Хорды АВ и СD пересекаются в точке S, при чем AS:SB = 2:3, DS = 12см, SC = 5см, найти АВ. Согласно свойству хорд AS x SB = CS x SD, тогда 2х * 3х = 5 * 12 6х 2 = 60 х 2 = 10 x = √10 Откуда AB = AS + SB AB = 2√10 + 3√10= 5√10 Окружность разделена на части, которые относятся как 3,5:5,5:3 и точки деления соединены между собой. Определить величину углов образовавшегося треугольника. Решение. Обозначим коэффициент пропорциональности дуг окружности, как х. Соединим центры окружности с концами дуг. Поскольку центральный угол равен градусной мере дуги, на которую опирается, то соотношение центральных углов окружности будет равно соотношению ее частей (дуг). Поскольку градусная мера окружности равна 360 градусам, то 3,5х + 5,5х + 3х = 360 12х = 360 х = 30 Откуда градусные величины центральных углов равны: 3 * 30 = 90 3,5 *30 = 105 5,5 *30 = 165 Углы образовавшегося треугольника являются углами, вписанными в окружность. Вписанный угол равен половине градусной меры дуги, на которую опирается. Откуда углы треугольника равны: 90 / 2 = 45 105 / 2 = 52,5 165 / 2 = 82,5 Ответ: Величина углов треугольника равна 45 ; 52,5 ; 82,5 ; Источник ← хорда крыла самолета что это хорда окружности что это → Вам также понравится Все что придумал ад для любви 15.05.202215.05.2022 admin 0 Воронежский юридический техникум после 9 что сдавать 15.05.202215.05.2022 admin 0 клюшка 130 см на какой рост 23.05.202223.05.2022 admin 0 Добавить комментарий Отменить ответ Ваш адрес email не будет опубликован. Обязательные поля помечены * Комментарий * Имя * Email * Сохранить моё имя, email и адрес сайта в этом браузере для последующих моих комментариев.