Графики каких движений представлены на рисунке в чем сходны и чем различаются

Контрольная работа №1 «Равномерное и равноускоренное движение. Графики движения»

Контрольная работа №1 «Равномерное и равноускоренное движение. Графики движения»

1. Приведите примеры задач, в которых Луну: а) можно считать материальной точкой; б) нельзя считать материальной точкой.

2. Начальная и конечная скорости движения тела соответственно равны 15 м/с и 10 м/с? Как движется это тело?

4. По данному графику проекции скорости построить графики для координаты и проекции ускорения.

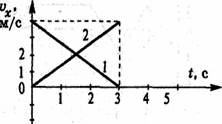
5. Графики каких движений представлены на рисунке? В чем сходны и чем различаются движения тел 1 и 2? Что можно сказать о путях, пройденных этими телами за время t1 от начала отсчета времени? Постройте графики пути для обоих тел.

Контрольная работа №1 «Равномерное и равноускоренное движение. Графики движения»

1. Ускорение тела равно 3 м/с2. Что это означает? Объясните.

2. Начальная и конечная скорости движения тела соответственно равны 15 м/с и 10 м/с? Как движется это тело?

3. Зависимость от времени координаты точки, движущейся вдоль оси х, имеет вид: х = 4 +5t + 2t2. Опишите характер движения. Каковы начальная скорость и ускорение? Запишите уравнение для проекции скорости.

4. По данному графику проекции ускорения построить графики для координаты и проекции скорости.

5. * Графики каких движений представлены на рисунке? В чем сходны и чем различаются движения тел 1 и 2? Что можно сказать о путях, пройденных этими телами за время t1 от начала отсчета времени? Постройте графики пути для обоих тел.

Контрольная работа №1 «Равномерное и равноускоренное движение. Графики движения»

1. Какую форму должна иметь траектория точки, чтобы пройденный этой точкой путь равнялся модулю перемещения?

2. Начальная и конечная скорости движения тела соответственно равны 15 м/с и 10 м/с? Как движется это тело?

4. По данному графику проекции скорости построить графики для координаты и проекции ускорения.

5. * Графики каких движений представлены на рисунке? В чем сходны и чем различаются движения тел 1 и 2? Что можно сказать о путях, пройденных этими телами за время t1 от начала отсчета времени? Постройте графики пути для обоих тел.

Контрольная работа №1 «Равномерное и равноускоренное движение. Графики движения»

1. Может ли человек, находясь на движущемся эскалаторе, быть в состоянии покоя относительно земли?

2. Начальная и конечная скорости движения тела соответственно равны 15 м/с и 10 м/с? Как движется это тело?

3. Автобус отъезжает от остановки с ускорением 2 м/с2. Какой путь он пройдет за 5 с?

4. По данному графику проекции скорости построить графики для координаты и проекции ускорения.

5. * Графики каких движений представлены на рисунке? В чем сходны и чем различаются движения тел 1 и 2? Что можно сказать о путях, пройденных этими телами за время t1 от начала отсчета времени? Постройте графики пути для обоих тел.

Источник

Вопросы.

1. Запишите формулу, по которой можно рассчитать проекцию вектора мгновенной скорости прямолинейного равноускоренного движения, если известны: а) проекция вектора начальной скорости и проекция вектора ускорения; б) проекция вектора ускорения при том, что начальная скорость равна нулю.

2. Что представляет собой график проекции вектора скорости равноускоренного движения при начальной скорости: а) равной нулю; б) не равной нулю?

3. Чем сходны и чем отличаются друг от друга движения, графики которых представлены на рисунках 11 и 12?

В обоих случаях движение происходит с ускорением, однако в первом случае ускорение положительно, а во-втором отрицательно.

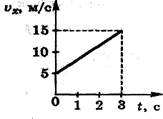
5. На рисунке 13 представлены графики зависимости модуля вектора скорости от времени при прямолинейном движении двух тел. С каким по модулю ускорением движется тело I? тело II?

Источник

ГРАФИЧЕСКОЕ ИЗОБРАЖЕНИЕ РАВНОУСКОРЕННОГО ДВИЖЕНИЯ

Начальный уровень:

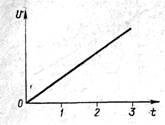
А1. Расскажите о движении те­ла, график проекции скоро­сти которого изображен на рисунке.

Рис.А1 Рис.А2 Рис.А3

А2. Расскажите о движении тела, график проекции скорости кото­рого изображен на рисунке.

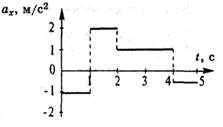
А3. Расскажите о движении тела, график проекции ускорения ко­торого изображен на рисунке.

А4. Как двигался автомобиль, график проекции скорости движения которого изобра­жен на рисунке?

А5. Расскажите о движении те­ла, график проекции ускоре­ния которого изображен на рисунке.

Рис.А4 Рис.А5 Рис.А6

А6. Как двигался велосипедист, график проекции скорости движения которого изобра­жен на рисунке?

Средний уровень:

Б1. (54.P) Зависимость скорости от времени при разгоне автомо­биля задана формулой v_x = 0,8 t. Построить график скорости и найти скорость в конце пятой секунды.

Б2. Зависимость скорости от времени движущегося тела задана формулой v_x = 1 + 2t. Опишите это движение (укажите значения характеризующих его величин), постройте график v_x (t).

Б3. (55.P) Скорость поезда за 20 с уменьшилась c 72 до 54 км/ч. Написать формулу зависимости скорости от времени v_x (t) и построить график этой зависимости.

Б4. (57.P) По заданным на рис.Б4 графикам написать урав­нения v_x = v_x (t).

Б5. По графикам, изображенным на рисунке, записать уравнения зависимости проекции скорости и координаты от времени v_x (t), x(t).

Б8. Зависимость скорости от времени движущегося тела задана формулой v_x = 4 + t. Опишите это движение (укажите значения характеризующих его величин), постройте график v_x (t).

Б9. По графикам, изобра­женным на рисунке, за­писать уравнения зави­симости проекции скоро­сти и координаты от времени v_x (t), x (t).

Б10. По графикам, изображенным на рисунке, записать уравнения зависимости проекции скорости и координаты от времени (v_x(t), x(t)).

Б12. По графикам, изображенным на рисунке, записать уравнения зависимости проекции скорости и координаты от времени v_x (t), x(t).

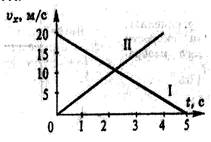
Рис.Б10 Рис.Б12 Рис.Б13

Б13. (59.P) По графикам зависимости а_х (t), приведенным на рис.Б13, а и б, построить графики зависимости v_x (t). считая, что в начальный момент времени (t = 0) скорость дви­жения материальной точки равна нулю.

Достаточный уровень:

В1. По данному графику проекции скорости построить графики для координаты и проекции ускорения.

В2. По данному графику проекции ускорения построить графики для координаты и проекции скорости.

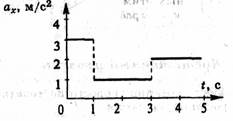
В3. По данному графику проекции скорости построить графики для координаты и проекции ускорения.

В4. По данному графику проекции ускорения построить графики для координаты и проекции скорости.

В5. По данному графику проекции скорости построить графики для координаты и проекции ускорения.

В6. По данному графику проекции ускорения построить графики для координаты и проекции скорости.

В7. По данному графику проекции скорости построить графики для координаты и проекции ускорения.

В8. Графики каких движений представлены на рисунке? В чем сходны и чем различаются движения тел 1 и 2? Что можно ска­зать о путях, пройденных этими телами за время 3c от начала отсчета времени? Постройте графики пути для обоих тел.

В9. (53.Т) С помощью графика скорости равноускоренного движения с начальной скоростью, равной нулю (рис.В9), покажите, что пути, пройденные телом за последовательные равные промежутки времени, пропорциональны ряду нечетных чисел.

В10. (38.Т) На рис.В10 даны графики ускорений четырех движущихся тел. Как движутся эти тела?

Высокий уровень:

Г1. Как двигался мотоцик­лист, график проекции скорости движения кото­рого изображен на рисун­ке? Начертите график пу­ти, соответствующий дан­ному графику.

Г2. По данному графику про­екции скорости построить графики для координаты и проекции ускорения.

Г3. По данному графику проекции ускорения построить, графики для координаты и проекции скорости.

Г4. По данному графику проекции скорости построить графики для координаты и проекции ускорения.

Г5. По данному графику проекции ускорения построить графики для координаты и проекции скорости.

Г6. По данному графику проекции ускорения построить графики для координаты и проекции скорости.

Олимпиадные задачи:

Д1. Как двигалось тело, график ускорения которого дан на рисунке. Начертите (качественно) графики скорости и пути, соответст­вующие данному графику ускорения.

Д2. На рисунке даны графики проекции скоростей для двух точек, движущихся по одной прямой от одного и того же начального по­ложения. Известны моменты времени t1 и t2. В какой момент вре­мени t3 точки встретятся? Построить графики движения x(t).

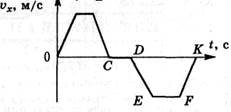
Д3. (51Т) На рисунке 17 дан график скорости тела, движущегося прямолинейно. Постройте график его перемещения и ускорения, если треугольники ОАВ, BCD, DEK равны.

Источник