График скорости прямолинейного движения материальной точки показан на рисунке чему равна скорость
Равномерное прямолинейное движение
1. Равномерное прямолинейное движение — движение, при котором тело за любые равные промежутки времени совершает одинаковые перемещения. Слова «любые равные» означают, что за каждый час, за каждую минуту, за каждые 30 минут, за каждую секунду, за каждую долю секунды тело совершает одинаковые перемещения.
Равномерное движение — идеализация, поскольку практически невозможно создать такие условия, чтобы движение тела было равномерным в течение достаточно большого промежутка времени. Реальное движение может лишь приближаться к равномерному движению с той или иной степенью точности.
2. Изменение положения тела в пространстве при равномерном движении может происходить с разной быстротой. Это свойство движения — его «быстрота» характеризуется физической величиной, называемой скоростью.
Скоростью равномерного прямолинейного движения называют векторную физическую величину, равную отношению перемещения ко времени, за которое это перемещение произошло.
Если за время \( t \) тело совершило перемещение \( \vec \) , то скорость его движения \( \vec >
3. Поскольку основной задачей механики является определение в любой момент времени положения тела, т.е. его координаты, необходимо записать уравнение зависимости координаты тела от времени при равномерном движении.
Полученная формула позволяет определить координату тела при равномерном движении в любой момент времени, если известны начальная координата и проекция скорости движения.
4. Зависимость координаты от времени можно представить графически.
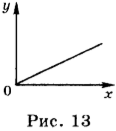
Предположим, что тело движется из начала координат вдоль положительного направления оси ОХ с постоянной скоростью. Проекция скорости на ось ОХ равна 4 м/с. Уравнение движения в этом случае имеет вид: \( x \) = 4 м/с · \( t \) . Зависимость координаты от времени — линейная. Графиком такой зависимости является прямая линия, проходящая через начало координат (рис. 13).
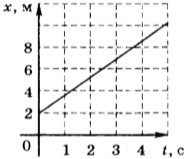
Для того чтобы её построить, необходимо иметь две точки: одна из них \( t \) = 0 и \( x \) = 0, а другая \( t \) = 1 с, \( x \) = 4 м. На рисунке приведён график зависимости координаты от времени, соответствующий данному уравнению движения.
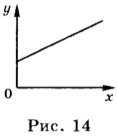
Если в начальный момент времени координата тела \( x_0 \) = 2 м, а проекция его скорости \( v_x \) = 4 м/с, то уравнение движения имеет вид: \( x \) = 2 м + 4 м/с · \( t \) . Это тоже линейная зависимость координаты от скорости, и её графиком является прямая линия, проходящая через точку, для которой \( t \) = 0, \( x \) = 2 м (рис. 14).
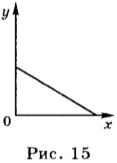
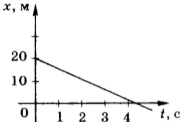
В том случае, если проекция скорости отрицательна, уравнение движения имеет вид: \( x \) = 2 м – 4 м/с · \( t \) . График зависимости координаты такого движения от времени представлен на рисунке 15.
Таким образом, движение тела может быть описано аналитически, т.е. с помощью уравнения движения (уравнения зависимости координаты тела от времени), и графически, т.е. с помощью графика зависимости координаты тела от времени.
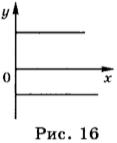
График зависимости проекции скорости равномерного прямолинейного движения от времени представлен на рисунке 16.
5. Ниже приведён пример решения основной задачи кинематики — определения положения тела в некоторый момент времени.
Задача. Два автомобиля движутся навстречу друг другу равномерно и прямолинейно: один со скоростью 15 м/с, другой — со скоростью 12 м/с. Определите время и место встречи автомобилей, если в начальный момент времени расстояние между ними равно 270 м.
При решении задачи целесообразно придерживаться следующей последовательности действий:
Применим эту последовательность действий к приведённой выше задаче.
Автомобили можно считать материальными точками, поскольку расстояние между ними много больше их размеров и размерами автомобилей можно пренебречь
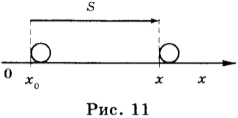
Система отсчёта связана с Землёй, ось \( Ox \) направлена в сторону движения первого тела, начало отсчёта координаты — т. \( O \) — положение первого тела в начальный момент времени.
Начальные условия: \( t \) = 0; \( x_ <01>\) = 0; \( x_ <02>\) = 270.
Уравнения для каждого тела с учётом начальных условий: \( x_1=v_1t \) ; \( x_2=l-v_2t \) . В месте встречи тел \( x_1=x_2 \) ; следовательно: \( v_1t=l-v_2t \) . Откуда \( t=\frac
ПРИМЕРЫ ЗАДАНИЙ
Часть 1
1. Чему равна проекция скорости равномерно движущегося автомобиля, если проекция его перемещения за 4 с равна 80 м?
1) 320 м/с
2) 80 м/с
3) 20 м/с
4) 0,05 м/с
2. Чему равен модуль перемещения мухи за 0,5 мин., если она летит со скоростью 5 м/с?
1) 0,25 м
2) 6 м
3) 10 м
4) 150 м
1) \( v_1=v_2 \)
2) \( v_1=2v_2 \)
3) \( 2v_1=v_2 \)
4) \( 1,2v_1=10v_2 \)
1) \( v_1=v_2 \)
2) \( v_1=2v_2 \)
3) \( 3v_1=v_2 \)
4) \( 2v_1=v_2 \)
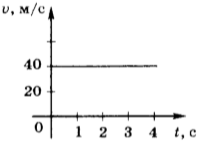
5. На рисунке приведён график зависимости модуля скорости равномерного движения от времени. Модуль перемещения тела за 2 с равен
1) 20 м
2) 40 м
3) 80 м
4) 160 м
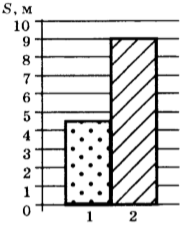
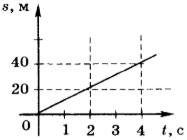
6. На рисунке приведён график зависимости пути, пройденного телом при равномерном движении от времени. Модуль скорости тела равен
1) 0,1 м/с
2) 10 м/с
3) 20 м/с
4) 40 м/с
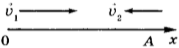
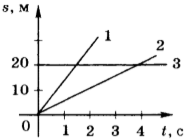
7. На рисунке приведены графики зависимости пути от времени для трёх тел. Сравните значения скорости \( v_1 \) , \( v_2 \) и \( v_3 \) движения этих тел.
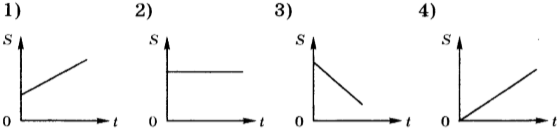
8. Какой из приведённых ниже графиков представляет собой график зависимости пути от времени при равномерном движении тела?
9. На рисунке приведён график зависимости координаты тела от времени. Чему равна координата тела в момент времени 6 с?
1) 9,8 м
2) 6 м
3) 4 м
4) 2 м
10. Уравнение движения тела, соответствующее приведённому в задаче 9 графику, имеет вид
1) \( x=1t \) (м)
2) \( x=2+3t \) (м)
3) \( x=2-1t \) (м)
4) \( x=4+2t \) (м)
11. Установите соответствие между величинами в левом столбце и зависимостью значения величины от выбора системы отсчёта в правом столбце. В таблице под номером элемента знаний левого столбца запишите соответствующий номер выбранного вами элемента правого столбца.
ВЕЛИЧИНА
A) перемещение
Б) время
B) скорость
ЗАВИСИМОСТЬ ОТ ВЫБОРА СИСТЕМЫ ОТСЧЁТА
1) зависит
2) не зависит
12. На рисунке приведён график зависимости координаты тела от времени. Какие выводы можно сделать из анализа графика? Укажите два правильных ответа.
1) тело двигалось все время в одну сторону
2) в течение четырёх секунд модуль скорости тела уменьшался, а затем увеличивался
3) проекция скорости тела все время была положительной
4) проекция скорости тела в течение четырёх секунд была положительной, а затем — отрицательной
5) в момент времени 4 с тело остановилось
Часть 2
13. Два автомобиля движутся друг за другом равномерно и прямолинейно: один со скоростью 20 м/с, другой — со скоростью 15 м/с. Через какое время второй автомобиль догонит первый, если в начальный момент времени расстояние между ними равно 100 м?
График скорости прямолинейного движения материальной точки показан на рисунке чему равна скорость
На рисунке приведён график зависимости модуля средней скорости Vр материальной точки от времени t при прямолинейном движении. Из приведённого ниже списка выберите все правильные утверждения и укажите их номера.
3) За первые 3 с движения материальная точка проходит путь 8 м.
4) За первые 2 с движения материальная точка проходит путь 12 м.
5) Модуль начальной скорости материальной точки равен 2 м/с.
При равноускоренном движении средняя скорость равна полусумме начальной и конечной скорости. Найдем, чему равна скорость тела в момент времени t = 1 c:
Таким образом, ускорение тела равно
Путь — это произведение средней скорости на затраченное время
Обратите внимание, что на графике приведена зависимость средней скорости от времени, а не просто скорости. Наклон этого графика не равен ускорению.
Грузик массой m = 100 г неподвижно висит на лёгкой абсолютно упругой гибкой резинке с коэффициентом упругости k = 100 Н/м в поле силы тяжести с ускорением свободного падения g. Грузик поднимают из этого положения вертикально вверх на высоту h = 80 см, меньшую длины резинки, и отпускают без начальной скорости. Найдите время движения грузика вниз до точки его остановки. Начальной деформацией резинки при покоящемся грузике можно пренебречь.
Какие законы Вы используете для описания движения груза на резинке? Обоснуйте их применение к данному случаю.
Обоснование. Грузик движется поступательно, поэтому его можно принять за материальную точку. На первом этапе движения грузика на него действует только сила тяжести, т. к. сопротивлением воздуха мы пренебрегаем. Следовательно, на этом этапе грузик движется с ускорением свободного падения. И для описания движения тела можно применять законы прямолинейного равноускоренного движения.
На втором этапе движения резинка упруго деформируется, в результате чего на грузик начинает действовать изменяющаяся по модулю и направлению сила упругости, для которой справедлив закон Гука. Таким образом, второй этап движения представляет собой механические колебания груза на резинке. Т. к. сила тяжести не меняется по модулю и направлению, то она не влияет на характер колебаний грузика. В инерциальной системе отсчета возможно применение законов колебательного движения.
Перейдем к решению.
1. Введём неподвижную декартову систему координат с вертикальной осью ОХ, направленной вниз, причём начало координат поместим на уровне начального положения грузика.
2. После подъёма и отпускания грузика его движение вниз в поле силы тяжести разбивается на две стадии: вначале он свободно падает с ускорением g с высоты h до точки x = 0 (поскольку начальной деформацией резинки можно пренебречь) за время
что следует из формул кинематики равноускоренного движения.
3. Затем резинка начинает растягиваться, а грузик — тормозиться вплоть до остановки в нижней точке его движения. Поскольку начальное растяжение резинки компенсирует вес грузика, то на второй стадии можно считать, что действует только упругая сила, и уравнение движения (второй закон Ньютона) в проекции на ось ОХ имеет вид:
что является уравнением гармонических колебаний с периодом
4. С учётом начальных условий закон движения грузика на втором этапе представляет собой 1/4 часть периода синусоиды и происходит за время
5. Таким образом, искомое время движения грузика вниз до точки остановки равно
6. Подставляя численные данные из условия, получаем:
Ответ:
График скорости прямолинейного движения материальной точки показан на рисунке чему равна скорость
1 мин = 60 с; 1 ч = 3600 с; 1 км = 1000 м; 1 м/с = 3,6 км/ч.
ПРИМЕРЫ РЕШЕНИЯ ТИПОВЫХ ЗАДАЧ
Типовая задача «Уравнение координаты (нахождение неизвестной величины)»
Задача № 1. В начальный момент времени тело находилось в точке с координатой 5 м, а через 2 мин от начала движения — в точке с координатой 95 м. Определите скорость тела и его перемещение.
Типовая задача «Уравнение координаты. Движение двух тел»
Задача № 2. Движение двух тел задано уравнениями x1 = 20 – 8t и х2 = –16 + 10t (время измеряется в секундах, координата — в метрах). Определите для каждого тела начальную координату, проекцию скорости, направление скорости. Вычислите время и место встречи тел.
Типовая задача «График координаты»
Задача № 3. Движение тела задано графиком координаты (зависимости координаты от времени). По графику определите: а) начальную координату тела; б) проекцию скорости тела; в) направление движения тела (по оси х или против оси х); г) запишите уравнение координаты.
Типовая задача «График координаты. Движение нескольких тел»
Задача № 4. На рисунке изображены графики движения трех тел. Изучив рисунок, для каждого тела определите: а) начальную координату; б) скорость; в) направление движения; г) запишите уравнение координаты.
ЗАДАЧИ ПОСЛОЖНЕЕ
Задача № 5. На рисунке представлены графики зависимости координаты х от времени t для пяти тел. Определите скорости этих тел. Проанализируйте точки пересечения графиков. Постройте графики зависимости скорости от времени.
РЕШЕНИЕ:
РЕШЕНИЕ:
Алгоритм решения ЗАДАЧИ на Прямолинейное равномерное движение.
Задачи, описывающие движение, содержат два типа величин: векторные (имеющие направление) и скалярные (выражающиеся только числом). К векторным величинам при описании равномерного прямолинейного движения относятся скорость и перемещение.
Для перехода от векторов к скалярам выбирают координатную ось и находят проекции векторов на эту ось, руководствуясь следующим правилом: если вектор сонаправлен с осью, то его проекция положительна, если противоположно направлен — отрицательна. (Могут быть и более сложные случаи, когда вектор не параллелен координатной оси, а направлен к ней под некоторым углом.) Поэтому при решении задачи обязательно нужно сделать чертеж, на котором изобразить направления всех векторов и координатную ось. При записи «дано» следует учитывать знаки проекций.
При решении задач все величины должны выражаться в международной системе единиц (СИ), если нет специальных оговорок.
В решении задачи единицы величин не пишутся, а записываются только после найденного значения величины.
Это конспект по теме «ЗАДАЧИ на Прямолинейное равномерное движение с решениями». Выберите дальнейшие действия: