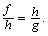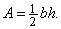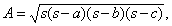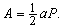Геометрия это наука о чем

Геометрия

Содержание

Классификация

Общепринятую в наши дни классификацию различных разделов геометрии предложил Феликс Клейн в своей «Эрлангенской программе» (1872). Согласно Клейну, каждый раздел изучает те свойства геометрических объектов, которые сохраняются (инвариантны) при действии некоторой группы преобразований, специфичной для каждого раздела. В соответствии с этой классификацией, в классической геометрии можно выделить следующие основные разделы.

Современная геометрия включает в себя следующие дополнительные разделы.

По используемым методам выделяют также такие инструментальные подразделы.

История

Традиционно считается, что родоначальниками геометрии как систематической науки являются древние греки, перенявшие у египтян ремесло землемерия и измерения объёмов тел и превратившие его в строгую научную дисциплину. При этом античные геометры от набора рецептов перешли к установлению общих закономерностей, составили первые систематические и доказательные труды по геометрии. Центральное место среди них занимают составленные около 300 до н. э. «Начала» Евклида. Этот труд более двух тысячелетий считался образцовым изложением в духе аксиоматического метода: все положения выводятся логическим путём из небольшого числа явно указанных и не доказываемых предположений — аксиом.

Геометрия греков, называемая сегодня евклидовой, или элементарной, занималась изучением простейших форм: прямых, плоскостей, отрезков, правильных многоугольников и многогранников, конических сечений, а также шаров, цилиндров, призм, пирамид и конусов. Вычислялись их площади и объёмы. Преобразования в основном ограничивались подобием.

Средние века немного дали геометрии, и следующим великим событием в её истории стало открытие Декартом в XVII веке координатного метода («Рассуждение о методе», 1637). Точкам сопоставляются наборы чисел, это позволяет изучать отношения между формами методами алгебры. Так появилась аналитическая геометрия, изучающая фигуры и преобразования, которые в координатах задаются алгебраическими уравнениями. Примерно одновременно с этим Паскалем и Дезаргом начато исследование свойств плоских фигур, не меняющихся при проектировании с одной плоскости на другую. Этот раздел получил название проективной геометрии. Метод координат лежит в основе появившейся несколько позже дифференциальной геометрии, где фигуры и преобразования все ещё задаются в координатах, но уже произвольными достаточно гладкими функциями.

Ф. Клейн в «Эрлангенской программе» систематизировал все виды однородных геометрий; согласно ему геометрия изучает все те свойства фигур, которые инвариантны относительно преобразований из некоторой группы. При этом каждая группа задаёт свою геометрию. Так, изометрии (движения) задаёт евклидову геометрию, группа аффинных преобразований — аффинную геометрию.

Источник

Наука геометрия

Помните: точка, прямая, отрезок, угол, аксиома, теорема, доказательство? Да-да, это всё оттуда.

Кто придумал геометрию?

Достоверно известно, что наука геометрия появилась примерно в 300 году до нашей эры. И спасибо за это стоит сказать великому ученому, философу Евклиду. Именно он собрал все познания в единую науку, составив так называемые «Элементы» Евклида. Ими на протяжении двух тысяч лет пользовались все учёные мира.

Зачем нужна геометрия современным детям?

Главная задача при изучении геометрии состоит в том, чтобы:

Многие актуальные сегодня профессии просто немыслимы без знаний геометрии. Это и дизайнер, и конструктор, и модельер, и инженер, и простой строитель. А как мужчина построит дом, если не сможет вычислить необходимые параметры? Сделать элементарный ремонт в квартире, и то нужно просчитать площадь и закупить материалы.

Да и никто не поспорит, что геометрия очень хорошо тренирует мозг. Лишних и ненужных знаний не бывает. Сегодня кажется, что геометрия нам ни к чему, а завтра жизнь приподнесет сюрприз, и без нее мы не сможем мыслить свои будни. Кто знает, что будет завтра? Поэтому учиться никогда не поздно! Учитесь, господа!

Надо признаться, что попытка трактовать естественные проблемы без геометрии есть попытка сделать невозможное (Галилео Галилей)

Существует ли самое большое число, читайте здесь.

Источник

Что такое геометрия? Наука геометрия

Геометрия является важной частью математики, которую начинают изучать в школах с 7 класса в качестве отдельного предмета. Что такое геометрия? Что она изучает? Какие полезные выводы можно из нее извлечь? Все эти вопросы подробно рассматриваются в статье.

Понятие о геометрии

Вам будет интересно: Гудериан Гейнц: биография, личная жизнь, семья, карьера

В ходе своего развития геометрия обзавелась набором понятий, которыми она оперирует с целью решения различных задач. К таким понятиям относятся точка, прямая, плоскость, поверхность, отрезок, окружность, кривая, угол и другие. Основой этой науки являются аксиомы, то есть концепции, связывающие геометрические понятия в рамках утверждений, которые принимаются в качестве истинных. На основании аксиом строятся и доказываются теоремы.

Когда появилась эта наука

Вам будет интересно: «Временный» или «временной»: как правильно? Разница между словами

Что такое геометрия с точки зрения истории? Здесь следует сказать, что она является очень древним учением. Так, ее использовали древние вавилоняне при определении периметров и площадей простых фигур (прямоугольников, трапеций и др.). Развита она была и в Древнем Египте. Достаточно вспомнить знаменитые пирамиды, строительство которых было бы невозможно без знания свойств объемных фигур, а также без умения ориентироваться на местности. Отметим, что знаменитое число «пи» (его приблизительное значение), без которого невозможно определить параметры круга, было известно египетским жрецам.

Разрозненные знания о свойствах плоских и объемных тел были собраны в единую науку только во времена Античной Греции благодаря деятельности ее философов. Самым важным трудом, на котором основываются современные геометрические учения, являются «Элементы» Евклида, которые были им составлены приблизительно в 300 году до нашей эры. Около 2000 лет этот трактат являлся основой для каждого ученого, который занимался исследованием пространственных свойств тел.

В XVIII веке французский математик и философ Рене Декарт заложил основы так называемой аналитической науки геометрии, которая описывала с помощью численных функций любой пространственный элемент (прямую, плоскость и так далее). С этого времени начинают появляться многие ветви в геометрии, причиной существования которых является пятый постулат в «Элементах» Евклида.

Евклидова геометрия

Что такое геометрия Евклида? Это достаточно стройное учение о пространственных свойствах идеальных объектов (точек, прямых, плоскостей и т.д.), которое основывается на 5 постулатах или аксиомах, изложенных в труде под названием «Элементы». Аксиомы приведены ниже:

Евклидова геометрия составляет основу любого современного школьного курса по этой науке. Более того, именно ею человечество пользуется в ходе своей жизнедеятельности при конструировании зданий и сооружений и при составлении топографических карт. Здесь важно отметить, что набор постулатов в «Элементах» не является полным. Он был расширен немецким математиком Давидом Гильбертом в начале XX века.

Виды евклидовой геометрии

Мы разобрались, что такое геометрия. Рассмотрим, какие ее виды бывают. В рамках классического учения принято выделять два вида этой математической науки:

Неевклидовы геометрии

Что такое геометрия в ее широком понимании? Помимо привычной нам науки о пространственных свойствах тел, существуют также неевклидовы геометрии, в которых пятый постулат в «Элементах» нарушается. К ним относятся эллиптическая и гиперболическая геометрии, которые были созданы в XIX веке немецким математиком Георгом Риманом и русским ученым Николаем Лобачевским.

Изначально полагали, что неевклидовы геометрии имеют узкую область применения (например, в астрономии при изучении небесной сферы), а само физическое пространство является евклидовым. Ошибочность последнего утверждения показал Альберт Эйнштейн в начале XX века, разработав свою теорию относительности, в которой он обобщил понятия пространства и времени.

Геометрия в школе

Как было сказано выше, изучение в школе геометрии начинается с 7 класса. При этом школьникам демонстрируют основы планиметрии. Геометрия 9 класса уже включает изучение трехмерных тел, то есть стереометрию.

Главная задача школьного курса состоит в том, чтобы развить у школьников абстрактное мышление и воображение, а также научить их мыслить логически.

Многие исследования показали, что при изучении этой науки у школьников наблюдаются проблемы с абстрактным мышлением. Когда формулируется для них геометрическая задача, они часто не понимают ее суть. У старшеклассников к проблеме с воображением добавляются трудности понимания математических формул для определения объема и площади поверхности разверстки пространственных фигур. Часто старшеклассники при изучении геометрии 9 класса не знают, какой формулой следует воспользоваться в конкретном случае.

Школьные учебники

Существует большое количество учебных пособий для обучения школьников этой науке. Одни из них дают только базовые знания, например, учебники Л. С. Атанасяна или А. В. Погорелова. Другие преследуют цель углубленного изучения науки. Здесь можно выделить учебник А. Д. Александрова или полный курс геометрии Бевза Г. П.

Поскольку в последние годы для сдачи всех экзаменов в школе введен единый стандарт ЕГЭ, стали необходимы учебники и решебники, которые позволяют ученику быстро самостоятельно разобраться с необходимой темой. Хорошим примером таких пособий можно назвать геометрию Ершовой А. П., Голобородько В. В.

Любой из названных выше учебников имеет как положительные, так и отрицательные отзывы со стороны учителей, поэтому преподавание в школе геометрии часто осуществляется с использованием нескольких учебников.

Источник

ГЕОМЕТРИЯ

ГЕОМЕТРИЯ, раздел математики, занимающийся изучением свойств различных фигур (точек, линий, углов, двумерных и трехмерных объектов), их размеров и взаимного расположения. Для удобства преподавания геометрию подразделяют на планиметрию и стереометрию. В планиметрии рассматриваются фигуры на плоскости; в стереометрии изучаются пространственные фигуры.

ИСТОРИЯ

Египет.

Если не учитывать весьма скромный вклад древних обитателей долины между Тигром и Евфратом и Малой Азии, то геометрия зародилась в Древнем Египте до 1700 до н.э. Во время сезона тропических дождей Нил пополнял свои запасы воды и разливался. Вода покрывала участки обработанной земли, и в целях налогообложения нужно было установить, сколько земли потеряно. Землемеры использовали в качестве измерительного инструмента туго натянутую веревку. Еще одним стимулом накопления геометрических знаний египтянами стали такие виды их деятельности, как возведение пирамид и изобразительное искусство.

Основным источником наших знаний о древнеегипетской геометрии является относящийся примерно к 1700 до н.э. папирус Ринда, названный по имени владельца, египтолога Ринда (этот папирус также называется папирусом Ахмеса) и хранящийся ныне в Лондоне в Британском музее. Папирус Ринда свидетельствует о том, что древних египтян интересовали главным образом практические аспекты геометрии и что при накоплении геометрических фактов египтяне почти всецело руководствовались интуицией, экспериментом и приближенными представлениями.

Греция.

Около 600 до н.э. ионийские греки, совершившие путешествие в Египет, привезли на родину первые сведения о геометрии. Самым известным путешественником в Египет был Фалес (ок. 640 – ок. 546 до н.э.). Он был преуспевающим купцом, посвятившим последние годы жизни науке и политике. Фалес первым начал доказывать истинность геометрических соотношений, последовательно выводя их логически из некоторого набора общепринятых утверждений, называемых аксиомами или постулатами. Этот метод дедуктивного рассуждения, которому предстояло стать доминирующим в геометрии и фактически – во всей математике, сохраняет свое фундаментальное значение и в наши дни.

Одним из наиболее знаменитых учеников Фалеса был Пифагор (ок. 570 – ок. 500 до н.э.). Он много путешествовал, а потом поселился в Кротоне, в Италии, где основал общество, занимавшееся изучением арифметики, музыки, геометрии и астрономии. Пифагор и его последователи доказали много новых теорем о треугольниках, окружностях, пропорциях и некоторых трехмерных телах. Пифагор доказал также знаменитую теорему, носящую ныне его имя, согласно которой площадь квадрата, построенного на гипотенузе прямоугольного треугольника, равна сумме площадей квадратов, построенных на катетах.

Пифагор умер в изгнании, но его влияние на греческих математиков ощущалось на протяжении многих веков. После его кончины в Элее (город в Италии) новыми центрами развивающейся геометрии становились по очереди Афины и Александрия. Архит Тарентский (ок. 428 – ок. 365 до н.э.) и Гиппий Элидский (р. ок. 425 до н.э.) затратили много усилий на решение трех задач, игравших важную роль в древнегреческой математике: это задачи о трисекции угла, о построении квадрата, площадь которого равна площади данного круга (задача о квадратуре круга), и о построении куба, имеющего вдвое больший объем, чем данный куб (задача об удвоении куба). Хотя ныне известно, что с помощью циркуля и линейки (единственных орудий геометрических построений, известных древнегреческим математикам) эти задачи решить нельзя, тем не менее попытки это сделать не были напрасны. Они стимулировали изучение конических сечений и способствовали совершенствованию математических методов.

Александрия.

Афинская школа числила в своих рядах таких великих людей, как Платон и Аристотель. После смерти Аристотеля центр научной мысли переместился в Александрию (Египет), где в начале 3 в. до н.э. был основан знаменитый Александрийский Мусейон – один из главных научных центров античного мира. Живший в Александрии математик Евклид (3 в. до н.э.), биографические сведения о котором крайне скудны, собрал в 13 книгах своего сочинения значительную часть математических знаний того времени. Семь книг из 13 были посвящены геометрии, предмет которой был им тщательно и систематически изложен, различные утверждения и теоремы расположены в определенном порядке и перенумерованы. Была включена также теория пространственных тел, ограниченных плоскими поверхностями. Называлось это великое сочинение Начала, и последующие издания, точно придерживающиеся оригинала, стали основой обучения геометрии вплоть до нашего времени. Величайшим математиком античности был грек Архимед (ок. 287–212 до н.э.). Кроме множества других полученных им научных результатов и открытий, Архимед расширил ту часть Начал Евклида, в которой рассматривались пространственные тела, включив в их число сферу, цилиндр и конус. Другими великими александрийскими геометрами были Аполлоний Пергский (3 в. до н.э.; конические сечения), Птолемей (2 в. н.э.; астрономия) и Папп (3 в. н.э.; плоские кривые высших порядков). В 641 н.э. арабы разграбили Александрию и разрушили Мусейон и его библиотеку. Впрочем, греческая математика вступила в период застоя еще в начале 4 в. н.э, после кончины Паппа. См. также ДРЕВНЯЯ ГРЕЦИЯ.

Средневековье.

После падения Александрии большинство работ древнегреческих математиков были рассеяны или утрачены. Некоторые из них, в том числе Начала Евклида, были переведены и изучались арабами и индийцами. И хотя эти народы породили нескольких великих математиков, среди которых наиболее известны индийские математики Ариабхата (ок. 476 – ок. 550) и Бхаскара II (ок. 1114–1185), все же их самой большой заслугой следует считать сохранение геометрии в период Средневековья.

После падения Римской империи в 5 в. наука в Европе долгое время находилась почти в полном забвении. В 12 и 13 вв. Начала были переведены с греческого и арабского на латынь и современные европейские языки, а геометрия вошла в программу монастырских школ. Первый из этих переводов был выполнен Аделардом Батским в 1120.

Новое время.

За последние 300 лет доказательная геометрия была существенно расширена, а по своим методам и степени общности результатов она стала заметно отличаться от элементарной геометрии (т.е. геометрии, изложенной в Началах). Французский математик Ж.Дезарг (1593–1662) в связи с развитием учения о перспективе занялся исследованием свойств геометрических фигур в зависимости от их проекций. Тем самым он заложил основу проективной геометрии, которая изучает те свойства фигур, которые остаются неизменными при различных проекциях. В 19 в. это направление получило существенное развитие. Проективная геометрия, конические сечения и новая геометрия треугольников и окружностей составили содержание современной т.н. чистой геометрии.

Тесно связанная с проективной, начертательная геометрия была введена французским математиком Г.Монжем (1746–1818). Эта новая область геометрии была связана с представлением изображений геометрических фигур на плоскости и определением геометрическими средствами расстояний, углов и линий пересечения. Начертательная геометрия представляет собой основу технического черчения.

В 1637 Р.Декарт (1596–1650), французский философ и математик, опубликовал свою Геометрию – первый труд по аналитической геометрии, позволивший применить в геометрии мощные алгебраические методы. Геометрические задачи всех видов теперь могли решаться в рамках единого подхода; кроме того, благодаря новым методам стала возможной постановка и решение новых задач, о которых древние не могли даже помыслить, но которые ныне находятся в самом центре математики и математической физики.

Со времен первого появления Начал математики тщетно пытались доказать пятый постулат Евклида: через точку, не лежащую на прямой, можно провести только одну прямую, ей параллельную. В 19 в. было доказано, что можно построить непротиворечивую геометрию, используя все аксиомы и постулаты Евклида и отрицание постулата о параллельных, а это означало, что искомого доказательства пятого постулата не существует. Любая такая непротиворечивая геометрия получила название неевклидовой геометрии. Около 1830 Я.Бойяи (1802–1860) и Н.И.Лобачевский (1792–1856) независимо друг от друга построили геометрию, использовавшую постулат, согласно которому через точку, лежащую вне прямой, можно провести много прямых, ей параллельных. В 1854 Б.Риман (1826–1866) сформулировал постулат, согласно которому через точку вне прямой невозможно провести ни одной параллельной, что дало начало т.н. римановой геометрии. Неевклидова математика расширилась и стала включать в себя тригонометрию, аналитическую и дифференциальную геометрии, охватив не только планиметрию, но и стереометрию, а также геометрию пространств размерности больше трех (геометрию гиперпространств). Евклидова и обе неевклидовы геометрии одинаково хорошо служат для описания той ограниченной области пространства, в которой мы живем, хотя геометрия Евклида проще по форме. В то же время при переходе к римановой геометрии некоторые современные физические теории существенно упрощаются. См. также МАТЕМАТИКИ ИСТОРИЯ.

ЭЛЕМЕНТАРНАЯ ПЛАНИМЕТРИЯ

Аксиомы и постулаты.

Существует набор исходных посылок, называемых аксиомами и постулатами, на которых базируется вся структура геометрии.

Аксиомы.

Аксиомы – это утверждения, принимаемые за истинные без доказательств. Аксиомы обычно подразделяются на две группы: общие, относящиеся ко всей математике, и геометрические.

К числу общих аксиом относятся следующие.

1. Равные одному и тому же равны между собой.
2. Если к равным прибавляются равные, то суммы будут равны.
3. Если от равных отнимаются равные, то остатки будут равны.
4. Если равные умножить на равные, то произведения будут равны.
5. Если равные разделить на равные, то частные будут равны. Деление на нуль запрещается.
6. Одинаковые степени равных, а также корни одинаковой степени из равных равны.
7. Целое больше любой своей части.
8. Целое равно сумме своих частей.

К числу геометрических аксиом относятся следующие.

1. Через любые две данные точки можно провести только одну прямую.
2. Геометрическую фигуру можно перемещать в пространстве, не изменяя ни ее размеров, ни ее формы.
3. Геометрические фигуры, которые совпадают после наложения, конгруэнтны (т.е. равны).
4. Прямая есть кратчайшее расстояние между двумя точками.

Постулаты.

Следующие постулаты касаются построений и принимаются за истинные без доказательств.

1. Через любые две данные точки можно провести прямую.
2. Прямая может быть продолжена бесконечно или же ограничена в любой своей точке.
3. Окружность может быть описана вокруг любой данной точки как центра и с любым радиусом.
4. Все прямые углы равны.
5. Через точку, не лежащую на прямой, можно провести одну и только одну прямую, ей параллельную.

Некоторые геометрические фигуры, построения и заключения.

Многие термины, используемые для описания фигур в геометрии, настолько фундаментальны, что определить их не представляется возможным. Все попытки сделать это приводили лишь к замене одних терминов другими, столь же неопределимыми, или к простому описанию некоторых свойств фигур. Например, термин «точка» не поддается определению.

Линии.

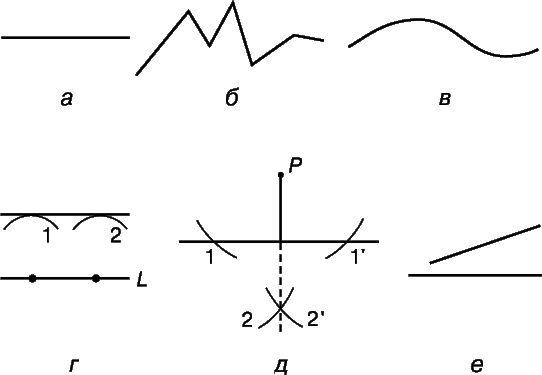
Термин «линия» (или «кривая» в широком смысле слова) не имеет определения, хотя мысленно линию можно представить как след движущейся точки. Бесчисленные попытки определить прямую линию (рис. 1,а) не имели успеха. Многие из этих попыток апеллировали к физическому эксперименту, например, «прямая – это туго натянутая линия». Чаще других приводится описание прямой, предложенное Архимедом: «Прямая – это кратчайшее расстояние между двумя точками». Это «определение», однако, лишь заменяет неопределяемое понятие прямизны столь же неопределяемым понятием расстояния. Предполагается, что прямая бесконечна, т.е. ее можно неограниченно продолжить в обе стороны. Часть прямой называется отрезком. Ломаная (рис. 1,б) состоит из прямолинейных отрезков. Кривой (рис. 1,в) называется линия, никакая часть которой не является прямой.

Как показано на рис. 1,г, 1,д и 1,е, прямые могут быть параллельными, перпендикулярными и наклонными. Параллельные прямые – это прямые, расстояние между которыми всюду одинаково. На рис. 1,г показано, как построить прямую, параллельную данной прямой L и отстоящую от нее на заданное расстояние. Берется окружность, радиус которой равен данному расстоянию. Проводятся две дуги с центрами в двух различных точках прямой L. Прямая, касательная к обеим дугам, и есть та прямая, которую требовалось построить.

На рис. 1,д показано, как построить прямую, проходящую через точку Р и перпендикулярную прямой L. Порядок, в котором делаются засечки дугами, указаны номерами [первыми следует провести (в любой последовательности) либо дугу 1, либо дугу 1ў]. Для проведения дуг 2 и 2ў циркуль устанавливается в точки пересечения прямой L дугами 1 и 1ў соответственно, радиусы остаются те же самые. Прямая, проходящая через точку Р и точку пересечения дуг 2 и 2ў, есть искомый перпендикуляр. Перпендикуляр – это кратчайшая линия, которую можно провести от точки до прямой, на которую он опущен, и расстояние от точки до прямой по определению равно длине перпендикуляра, опущенного из нее на прямую.

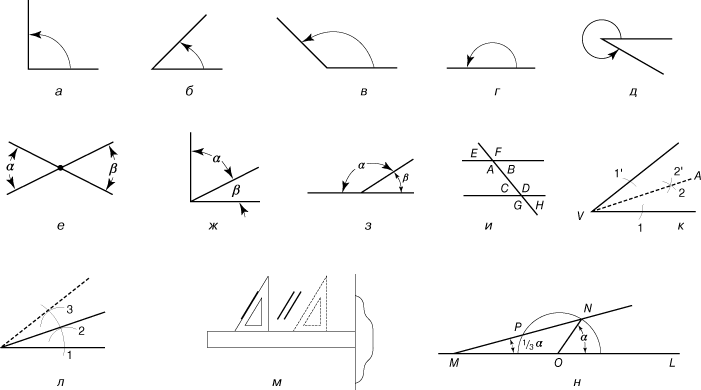
Углом называется фигура, образованная двумя полупрямыми, исходящими из одной точки. Эта точка называется вершиной угла, а полупрямые – сторонами угла. Если стороны угла перпендикулярны друг другу, то образуемый ими угол называется прямым (рис. 2,а). Углы меньше прямого называются острыми (рис. 2,б), а углы больше прямого – тупыми (рис. 2,в). Развернутым называется угол, обе стороны которого лежат на одной прямой (рис. 2,г); такой угол равен двум прямым углам. Биссектрисой угла называется прямая, проходящая через его вершину и делящая угол пополам. Углы можно измерять количественно, если определить единицу измерения угла (угол в один градус) как 1/180 развернутого угла. Таким образом, прямой угол содержит 90°, а угол на рис. 2,д содержит больше 180°, но меньше 360°.

На рис. 2,е, 2,ж, 2,з и 2,и показано, как соотносятся между собой углы некоторых фигур. Два угла называются вертикальными, если стороны одного угла являются дополнительными полупрямыми сторон другого (рис. 2,е). Вертикальные углы равны. Дополнительные углы в сумме составляют 90° (рис. 2,ж), а смежные углы в сумме дают 180° (рис. 2,з). Если прямая пересекает две параллельные прямые, как на рис. 2,и, то углы E, B, C и H равны, и углы F, A, D и G также равны между собой. Углы между параллельными (углы А, В, С, D на рисунке) называются внутренними, а углы, лежащие вне параллельных – внешними. Тот факт, что параллельные образуют с пересекающей их прямой равные углы, используется при вычерчивании параллельных прямых (рис. 2,м).

На рис. 2,к показано, как с помощью циркуля и линейки разделить пополам данный угол: прямая VA – биссектриса угла. На рис. 2,л показано, как удвоить данный угол.

Традиционно в элементарной геометрии выполнялись лишь геометрические построения, которые можно осуществить, используя только циркуль и линейку без делений. Общего подхода к таким построениям не существует, и успех почти целиком зависит от настойчивости и изобретательности. Так, например, может показаться, что задача о разделении угла на три равные части, т.н. трисекция угла, достаточно легка, поскольку сходная с ней задача деления угла пополам решается довольно просто. Однако на протяжении веков все усилия как любителей, так и профессионалов осуществить трисекцию угла неизменно оканчивались неудачей. Правда, эту задачу удалось решить, используя некоторые плоские кривые высших порядков, например, конхоиду и квадратриссу, а Архимед показал, как можно было бы решить задачу о трисекции угла с помощью линейки с двумя отметинами (рис. 2,н). В предложенном им решении задачи на ребре линейки откладывается расстояние МР, равное радиусу ON. Линейка кладется так, чтобы ее край проходил через точку N, тогда точка М попадает на продолжение прямой OL, а точка P – на окружность. Задача о трисекции угла эквивалентна поиску геометрического построения, позволяющего находить корни уравнения x 3 – 2 = 0. В 1837 вопрос о трисекции был окончательно решен французским математиком П.Ванцелем, давшим строгое доказательство невозможности точной трисекции угла в общем случае с помощью циркуля и линейки.

Треугольники.

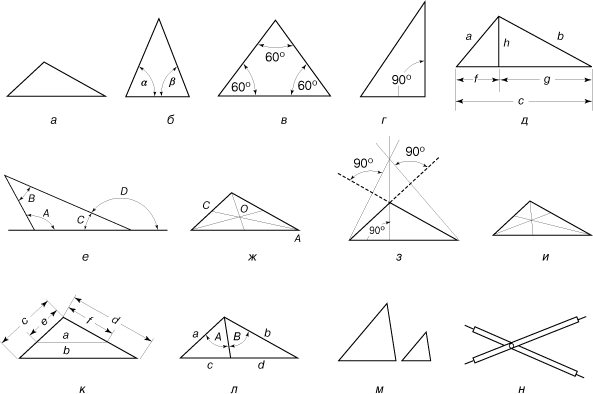
Треугольником называется плоская фигура, ограниченная тремя прямыми. У треугольника могут быть три неравные стороны (разносторонний треугольник), две равные стороны (равнобедренный треугольник) или три равные стороны (равносторонний треугольник) (рис. 3,а, 3,б, 3,в). В равнобедренном треугольнике углы, лежащие против равных сторон (углы a и b на рис. 3,б), равны; в равностороннем треугольнике все углы равны.

Длина перпендикуляра h, опущенного из вершины прямого угла на гипотенузу, есть среднее пропорциональное длин отрезков, на которые основание перпендикуляра делит гипотенузу:

Углы внутри треугольника называются внутренними; углы, которые образуются, если стороны треугольника продлить за их вершины, называются внешними (рис. 3,е). Сумма внутренних углов треугольника равна развернутому углу. Любой внешний угол равен сумме двух внутренних углов, не имеющих с ним общей вершины (РD = РA + РB).

Отрезок прямой, соединяющий вершину треугольника с серединой противолежащей стороны, называется медианой. Три медианы треугольника пересекаются в одной точке, которая делит каждую медиану в отношении 2:1, считая от вершины. Например, на рис. 3,ж отрезок АО составляет 2/3 от длины отрезка АС. Точка пересечения медиан является также центром тяжести треугольника (треугольник, вырезанный из однородного по толщине и плотности материала и подвешенный в этой точке, будет находиться в равновесии). Высотой треугольника называется перпендикуляр, опущенный из одной из его вершин на противоположную сторону (или ее продолжение). Все три высоты треугольника пересекаются в одной точке, которая называется ортоцентром (рис. 3,з); биссектрисы всех углов треугольника также пересекаются в одной точке, которая является центром вписанной окружности (рис. 3,и) и равноудалена от всех сторон треугольника.

Прямая, пересекающая треугольник и параллельная одной из его сторон, делит две другие стороны на пропорциональные отрезки. На рис. 3,к a/b = e/c = f/d. Биссектриса любого угла треугольника делит противоположную сторону на отрезки, пропорциональные длинам сторон, образующих угол. На рис. 3,л, если РA = РB, то c/a = d/b.

Два треугольника (любые фигуры) называются равными (или конгруэнтными), если они переводятся друг в друга преобразованиями движения. Преобразование одной фигуры в другую называется движением, если оно сохраняет расстояния между точками. Можно доказать три признака равенства треугольников: два треугольника равны, если 1) две стороны и угол между ними одного треугольника равны соответственно двум сторонам и углу между ними другого треугольника; 2) сторона и прилежащие к ней углы одного треугольника равны соответственно стороне и прилежащим к ним углам другого треугольника; и 3) три стороны одного треугольника равны соответственно трем сторонам другого треугольника. Если треугольники можно перевести друг в друга преобразованием движения, не выводящим их из плоскости, в которой оба они лежат, то они называются собственно конгруэнтными; если же один из треугольников необходимо перевернуть, то треугольники называются несобственно конгруэнтными.

Преобразование одной фигуры в другую называется преобразованием подобия, если при этом преобразовании расстояния между точками изменяются в одно и то же число раз. Две фигуры подобны, если они переводятся друг в друга преобразованием подобия.

Если два треугольника подобны (рис. 3,м), то их углы равны, а соответствующие стороны пропорциональны. Пропорциональным делителем, изображенным на рис. 3,н, пользуются для того, чтобы увеличить или уменьшить чертеж в требуемое число раз.

Площадь любого треугольника равна половине произведения его стороны на проведенную в ней высоту:

Если треугольник равносторонний, то его площадь равна 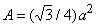, где а – длина стороны. Если а, b, c – длины сторон треугольника, то его площадь определяется по формуле

вывод которой приписывают Герону (s – полупериметр).

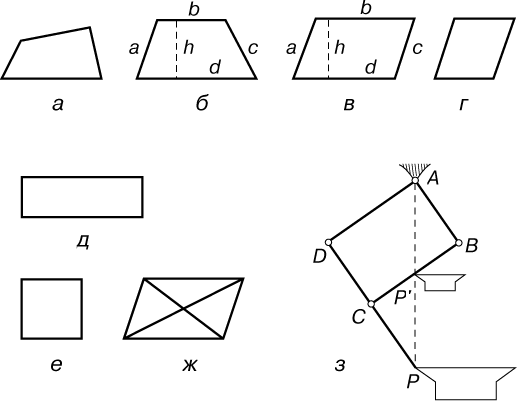
Четырехугольники.

Четырехугольником является всякая плоская фигура, ограниченная четырьмя прямыми (рис. 4). Параллелограммом называется четырехугольник, у которого противоположные стороны имеют равную длину. Ромб (рис. 4,г) – это параллелограмм, все стороны которого равны, а прямоугольник (рис. 4,д) – это параллелограмм, у которого все углы прямые. Диагонали параллелограмма (рис. 4,ж) в точке пересечения делятся пополам; в прямоугольнике диагонали равны. Трапецией называется четырехугольник, у которого две стороны параллельны, а две другие – непараллельны. Параллельные стороны называются основаниями. Площадь трапеции равна произведению высоты на полусумму ее оснований: A = h [(b + d)/2]. Площадь параллелограмма A = bh. Один из методов определения площади четырехугольника состоит в разбиении фигуры на два треугольника с помощью диагонали и в вычислении суммы площадей образовавшихся треугольников.

Интересным приложением свойств параллелограмма служит шарнирный пантограф (рис. 4,з), используемый для перечерчивания чертежей и других графических изображений в большем или меньшем масштабе. Пантограф представляет собой шарнирный механизм, имеющий форму параллелограмма, закрепленный в вершине А, со звеном DC, продленным до точки Р. Прямая РА пересекает звено СВ в точке Р ў. Звено СВ всегда параллельно звену DA, следовательно, треугольники PDA и PCP ў подобны. Поэтому CP ў = DAЧPC/PD, а эта величина постоянна, поэтому точка Р ў звена СВ также лежит на прямой, соединяющей точки Р и А. Из двух рассмотренных выше подобных треугольников следует, что отношение РА/Р ўА также постоянно. Следовательно, в любом положении пантографа перемещение точки Р ў пропорционально перемещению точки Р. Если точка Р движется по контуру какой-либо фигуры, то точка Р ў, в которой находится острие карандаша, повторяет без искажений этот контур в уменьшенном масштабе. Отношение масштабов оригинала и копии равно РА/Р ўА = PD/CD.

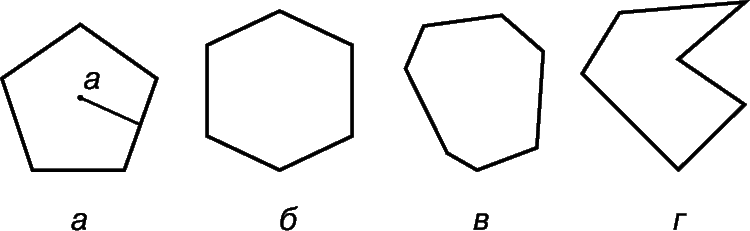
Многоугольники.

Многоугольником называется плоская фигура, ограниченная замкнутой ломаной линией, звенья которой называются сторонами. Многоугольник называется выпуклым, если он лежит в одной полуплоскости относительно любой прямой, содержащей его сторону. Выпуклый многоугольник называется правильным, если все стороны и углы его равны. Расстояние от центра правильного многоугольника до какой-либо его стороны равно радиусу вписанной в него окружности (обозначен на рис. 5,а буквой а). Площадь правильного многоугольника равна произведению половины радиуса на периметр:

В табл. 1 приведены названия и формулы для площадей некоторых правильных многоугольников (s означает длину стороны).

Таблица 1. НАЗВАНИЯ И ПЛОЩАДИ МНОГОУГОЛЬНИКОВ

Число сторон

Название многоугольника

Площадь правильного многоугольника

Источник