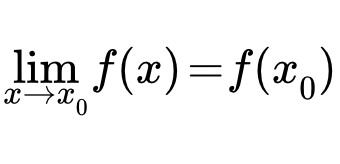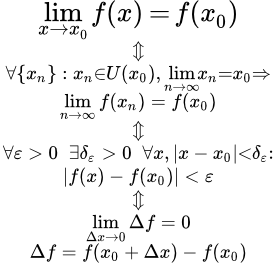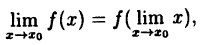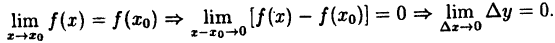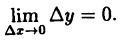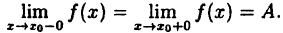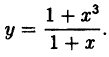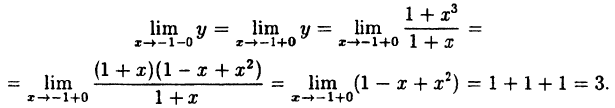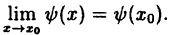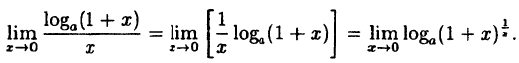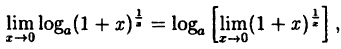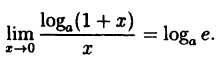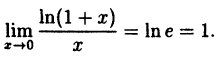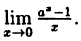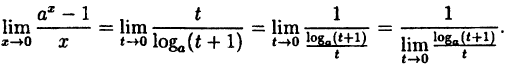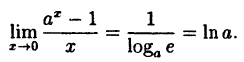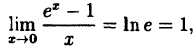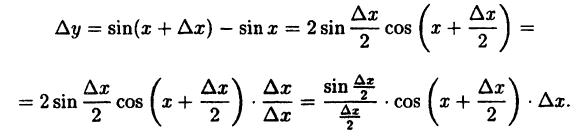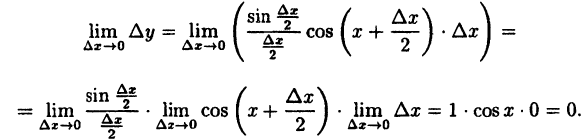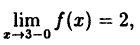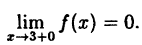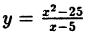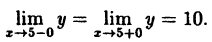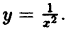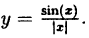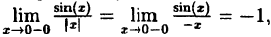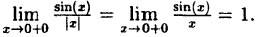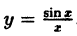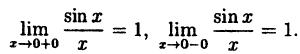Геометрическая непрерывность функции в точке x0 означает что ее график
Непрерывность функции в точке, разрывы первого и второго рода
Процесс исследования функции на непрерывность неразрывно связан с навыком нахождения односторонних пределов функции. Поэтому, чтобы приступить к изучению материала данной статьи, желательно предварительно разобрать тему предела функции.
Непрерывность функции в точке
Данное определение позволяет вывести следствие: значение предела функции в точках непрерывности совпадает со значением функции в этих точках.
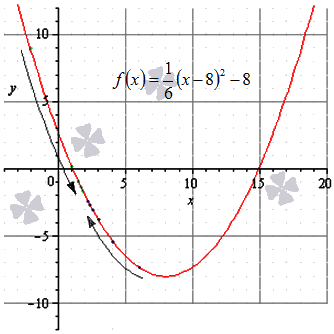
Решение
Соответствующая последовательность значений функций выглядит так:
на чертеже они обозначены зеленым цветом.
Соответствующая последовательность функций:
на рисунке обозначена синим цветом.
После вычисления значения функции в заданной точке очевидно выполнение равенства:
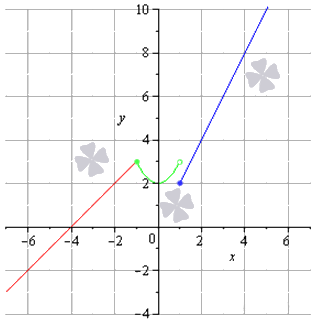
Устранимый разрыв первого рода
Решение
Ответ: пределы справа и слева являются равными, а заданная функция в точке х 0 = 5 не определена, т.е. в этой точке функция имеет устранимый разрыв первого рода.
Неустранимый разрыв первого рода
Неустранимый разрыв первого рода также определяется точкой скачка функции.
Решение
Определим пределы справа и слева от этих точек и значение заданной функции в этих точках:
Ответ: в конечном счете мы получили:
Нам остается только подготовить чертеж данного задания.
Разрыв второго рода (бесконечный разрыв)
Решение
Зададим произвольную последовательность значений аргумента, сходящуюся к х 0 слева. К примеру:
Ей соответствует последовательность значений функции:
Непрерывность функций – теоремы и свойства
Определение непрерывности функции
Определение непрерывности справа (слева)
Функция f ( x ) называется непрерывной справа (слева) в точке x 0 , если она определена на некоторой правосторонней (левосторонней) окрестности этой точки, и если правый (левый) предел в точке x 0 равен значению функции в x 0 :
.
Свойства непрерывных в точке функций
Свойство непрерывности слева и справа
Функция непрерывна в точке тогда и только тогда, когда она непрерывна в справа и слева.
Доказательства свойств приводятся на странице «Свойства непрерывных в точке функций».
Непрерывность сложной функции
Предел сложной функции
Точки разрыва
Определение точки разрыва 1-го рода
Точка называется точкой разрыва первого рода, если является точкой разрыва и существуют конечные односторонние пределы слева и справа :
.
Определение скачка функции
Скачком Δ функции в точке называется разность пределов справа и слева
.
Таким образом, точка устранимого разрыва – это точка разрыва 1-го рода, в которой скачек функции равен нулю.
Определение точки разрыва 2-го рода
Точка называется точкой разрыва второго рода, если она не является точкой разрыва 1-го рода. То есть если не существует, хотя бы одного одностороннего предела, или хотя бы один односторонний предел в точке равен бесконечности.
Свойства функций, непрерывных на отрезке
Вторая теорема Вейерштрасса о максимуме и минимуме непрерывной функции
Непрерывная на отрезке функция достигает на нем своих верхней и нижней граней или, что тоже самое, достигает на отрезке своего максимума и минимума.
Обратные функции
Аналогичным образом можно сформулировать теорему о существовании и непрерывности обратной функции на полуинтервале.
Свойства и непрерывность элементарных функций
Элементарные функции и обратные к ним непрерывны на своей области определения. Далее мы приводим формулировки соответствующих теорем и даем ссылки на их доказательства.
Показательная функция
Логарифм
Экспонента и натуральный логарифм
Степенная функция
Тригонометрические функции
Теорема о непрерывности тригонометрических функций
Тригонометрические функции: синус ( sin x ), косинус ( cos x ), тангенс ( tg x ) и котангенс ( ctg x ), непрерывны на своих областях определения.
Теорема о непрерывности обратных тригонометрических функций
Обратные тригонометрические функции: арксинус ( arcsin x ), арккосинус ( arccos x ), арктангенс ( arctg x ) и арккотангенс ( arcctg x ), непрерывны на своих областях определения.
Использованная литература:
О.И. Бесов. Лекции по математическому анализу. Часть 1. Москва, 2004.
Л.Д. Кудрявцев. Курс математического анализа. Том 1. Москва, 2003.
С.М. Никольский. Курс математического анализа. Том 1. Москва, 1983.
Определение непрерывности функции в точке
Непрерывность в точке
Определение непрерывности
Определение непрерывности функции в точке
Функция f ( x ) называется непрерывной в точке x 0 , если она определена на некоторой окрестности U ( x 0) этой точки, включая саму точку, и если предел при x стремящемся к x 0 существует и равен значению функции в x 0 :
.
Здесь подразумевается, что x 0 – это конечная точка. Значение функции в ней может быть только конечным числом.
Если привлечь сюда определение конечного предела функции в конечной точке, то можно дать развернутую формулировку определения непрерывности функции. Поскольку имеется два равносильных определения предела функции (по Коши и по Гейне), то можно дать, как минимум, еще два эквивалентных определения непрерывности.
Запишем эти определения с помощью логических символов существования и всеобщности.
По Гейне:
.
По Коши:
.
Определение отсутствия непрерывности
Непрерывность на концах отрезка
Определение непрерывности справа (слева)
Функция f ( x ) называется непрерывной справа (слева) в точке x 0 , если она определена на некоторой правосторонней (левосторонней) окрестности этой точки, и если правый (левый) предел в точке x 0 равен значению функции в x 0 :
.
Примеры
Пример 1
Используем определение по Гейне
Используем определение по Коши
Пример 2
Использованная литература:
О.И. Бесов. Лекции по математическому анализу. Часть 1. Москва, 2004.
Л.Д. Кудрявцев. Курс математического анализа. Том 1. Москва, 2003.
С.М. Никольский. Курс математического анализа. Том 1. Москва, 1983.
Непрерывность функции
Понятие непрерывности функции.
Функция \(f(x)\), определенная в некоторой окрестности точки \(a\), называется непрерывной в точке \(a\), если
$$
\displaystyle \lim_
$$
Таким образом, функция \(f\) непрерывна в точке \(a\), если выполнены следующие условия:
Определение непрерывности функции \(f(x)\) в точке \(a\), выраженное условием \eqref
Следует обратить внимание на то, что в определении непрерывности функции, в отличие от определения предела, рассматривается полная, а не проколотая окрестность точки \(a\), и пределом функции является значение этой функции в точке \(a\).
Назовем разность \(x-a\) приращением аргумента и обозначим \(\Delta x\), а разность \(f(x)-f(a)\) — приращением функции, соответствующим данному приращению аргумента \(\Delta x\), и обозначим \(\Delta y\). Таким образом,
$$
\Delta x=x-a,\;\Delta y=f(x)-f(a)=f(a+\Delta x)-f(a).\nonumber
$$
При этих обозначениях равенство \eqref
$$
\lim_<\Delta x\rightarrow 0>\Delta y=0.\nonumber
$$
Таким образом, непрерывность функции в точке означает, что бесконечно малому приращению аргумента соответствует бесконечно малое приращение функции.
Показать, что функция \(f(x)\) непрерывна в точке \(a\), если:
По аналогии с понятием предела слева (справа) вводится понятие непрерывности слева (справа). Если функция \(f\) определена на полуинтервале \((a-\delta,a]\) и \(\displaystyle \lim_
Аналогично, если функция \(f\) определена на полуинтервале \([a,a+\delta)\) и \(f(a+0)=f(a)\), то эту функцию называют непрерывной справа в точке \(a\).
Например, функция \(f(x)=[x]\) непрерывна справа в точке \(x=1\) и не является непрерывной слева в этой точке, так как \(f(1-0)=0,\;f(1+0)=f(1)=1\).
Очевидно, функция непрерывна в данной точке тогда и только тогда, когда она непрерывна как справа, так и слева в этой точке.
Точки разрыва.
Будем предполагать, что функция \(f\) определена в некоторой проколотой окрестности точки \(a\).
Точку \(a\) назовем точкой разрыва функции \(f\), если эта функция либо не определена в точке \(a\), либо определена, но не является непрерывной в точке \(a\).
Следовательно, \(a\) — точка разрыва функции \(f\), если не выполняется по крайней мере одно из следующих условий:
Если \(a\) — точка разрыва функции \(f\), причем в этой точке существуют конечные пределы слева и справа, то есть \(\displaystyle \lim_
Если \(x=a\) — точка разрыва первого рода функции \(f(x)\), то разность \(f(a+0)-f(a-0)\) называют скачком функции в точке \(a\). В случае когда \(f(a+0)=f(a-0)\), точку \(a\) называют точкой устранимого разрыва. Полагая \(f(a)=f(a+0)=f(a-0)=A\), получим функцию
$$
f(x)=\left\<\begin
$$
непрерывную в точке \(a\) и совпадающую с \(f(x)\) при \(x\neq a\). В этом случае говорят, что функция доопределена до непрерывности в точке \(a\).
Пусть \(x=a\) — точка разрыва функции \(f\), не являющаяся точкой разрыва первого рода. Тогда ее называют точкой разрыва второго рода функции \(f\). В такой точке хотя бы один из односторонних пределов либо не существует, либо бесконечен.
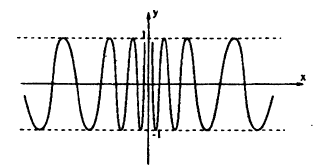
Например, для функции \(f(x)=\displaystyle x\sin<\frac<1>
$$
\overline
x\sin<\frac<1>
0,\;если\;x=0,
\end
$$
непрерывную в точке \(x=0\), так как
$$
\lim_
$$
Для функций \(\displaystyle \sin<\frac<1>
Если функция \(f\) определена на отрезке \([a,b]\) и монотонна, то она может иметь внутри этого отрезка точки разрыва только первого рода.
\(\circ\) Пусть \(x_0\) — произвольная точка интервала \((a,b)\). Функция \(f\) имеет в точке \(x_<0>\) конечные пределы слева и справа. Если, например, \(f\) — возрастающая функция, то
$$
f(x_<0>-0)\leq f(x_<0>)\leq f(x_<0>+0),\nonumber
$$
где \(f(x_<0>-0)\) и \(f(x_<0>+0)\) — соответственно пределы функции \(f\) слева и справа в точке \(x_<0>\).
Свойства функций, непрерывных в точке.
Локальные свойства непрерывной функции.
Если функция \(f\) непрерывна в точке \(a\), то она ограничена в некоторой окрестности этой точки, то есть
$$
\exists\delta>0\quad\exists C>0:\;\forall x\in U_<\delta>(a)\rightarrow|f(x)|\leq C\nonumber
$$
Если функция \(f\) непрерывна в точке \(a\), причем \(f(a)\neq 0\), то в некоторой окрестности точки \(a\) знак функции совпадает со знаком числа \(f(a)\), то есть
$$
\exists\delta>0:\quad\forall x\in U_<\delta>(a)\rightarrow \operatorname
$$
\(\circ\) Эти утверждения следуют из свойств пределов. \(\bullet\)
Непрерывность суммы, произведения и частного.
Если функции \(f\) и \(g\) непрерывны в точке \(a\), то функции \(f+g\), \(fg\) и \(f/g\) (при условии \(g(a)\neq 0\)) непрерывны в точке \(a\).
\(\circ\) Это утверждение следует из определения непрерывности и свойств пределов. \(\bullet\)
Непрерывность сложной функции.
Напомним, что такое сложная функция.
Пусть функции \(y=\varphi(x)\) и \(z=f(y)\) определены на множествах \(X\) и \(Y\) соответственно, причем множество значений функции \(\varphi\) содержится в области определения функции \(f\). Тогда функция, которая принимает при каждом \(x\in X\) значение \(F(x)=f(\varphi(x))\), называется сложной функцией или суперпозицией (композицией) функций \(\varphi\) и \(f\).
Если функция \(z=f(y)\) непрерывна в точке \(y_0\), а функция \(y=\varphi(x)\) непрерывна в точке \(x_0\), причем \(y_0=\varphi(x_0)\), то в некоторой окрестности точки \(x_0\) определена сложная функция \(f(\varphi(x_0))\), и эта функция непрерывна в точке \(x_0\).
\(\circ\) Пусть задано произвольное число \(\varepsilon>0\). В силу непрерывности функции \(f\) в точке \(y_0\) существует число \(\rho=\rho(\varepsilon)>0\) такое, что \(U_\rho(y_0)\subset D(f)\) и
$$
\forall y\in U_\rho(y_0)\rightarrow f(y)\in U_<\varepsilon>(z_<0>),\label
$$
где \(z_<0>=f(y_<0>)\).
В силу непрерывности функции \(\varphi\) в точке \(x_<0>\) для найденного в \eqref
$$
\forall x\in U_\delta(x_0)\rightarrow \phi (x)\in U_\rho (y_0).\label
$$
Из условий \eqref
$$
\forall x\in U_\delta(x_0)\rightarrow f(y)=f(\varphi(x))\in U_<\varepsilon>(z_<0>),\nonumber
$$
где \(z_0=f(\varphi(x_0))=f(y_<0>)\), то есть
$$
\forall \varepsilon>0\;\exists \delta>0:\quad \forall х\in U_\delta(x_0)\rightarrow f(\varphi(х))\in U_\varepsilon(\varphi(x_0)).\nonumber
$$
Это означает, в силу определения непрерывности, что функция \(f(\varphi(x))\) непрерывна в точке \(x_0\). \(\bullet\)
Соответствие между окрестностями точек \(x_0,\ y_0,\ z_0\) представлено на рис. 11.1. По заданному числу \(\varepsilon>0\) сначала находим \(\rho>0\), а затем для чисел \(\rho>0\) находим \(\delta>0\).
Рис. 11.1
Свойства функций, непрерывных на отрезке.
Функцию \(f(x)\) называют непрерывной на отрезке \([a,b]\), если она непрерывна в каждой точке интервала \((a,b)\) и, кроме того, непрерывна справа в точке \(a\) и непрерывна слева в точке \(b\).
Ограниченность непрерывной на отрезке функции.
Если функция \(f\) непрерывна на отрезке \([a,b]\), то она ограничена, то есть
$$
\exists C>0:\forall x\in[a,\ b]\rightarrow|f(x)|\leq C.\label
$$
\(\circ\) Предположим противное, тогда
$$
\forall C>0\;\exists x_
$$
Полагая в этом выражении \(C=1,2\ldots,n,\ldots,\) получим, что
$$
\forall n\in\mathbb
$$
Последовательность \(x_n\) ограничена, так как \(a\leq x_
$$
\lim_
$$
где в силу условия \eqref
$$
a\leq x_
$$
Из условий \eqref
$$
\displaystyle \lim_
$$
С другой стороны. утверждение \eqref
$$
|f(x_
$$
откуда следует, что \(\displaystyle \lim_
Теорема Вейерштрасса неверна для промежутков, не являющихся отрезками. Например, функция \(f(x)=\displaystyle \frac<1>
Достижимость точных граней.
Если функция \(f\) непрерывна на отрезке \([a,b]\), то она достигает своей точной верхней и нижней грани, то есть
$$
\exists\xi\in[a,b]:\quad f(\xi)=\sup_
$$
\(\circ\) Так как непрерывная на отрезке функция \(f(x)\) ограничена (теорема 3), то есть множество значений, принимаемых функцией \(f\) на отрезке \([a,b]\), ограничено, то существуют \(\displaystyle \sup_
Докажем утверждение \eqref
$$
\forall х\in [a,b]\rightarrow f(x)\leq M,\label
$$
$$
\forall\varepsilon>0\;\exists x(\varepsilon)\in[a,b]:\quad f(x(\varepsilon))>M-\varepsilon.\label
$$
Полагая \(\varepsilon=\displaystyle \frac<1><2>, \displaystyle \frac<1><3>,\ldots,\frac<1>
$$
x_n\in [a,b],\label
$$
$$
f(x_
$$
Из соотношений \eqref
$$
\forall n\in\mathbb
Теорема 4 неверна для интервалов: функция, непрерывная на интервале, может не достигать своих точных граней. Например, функция \(f(x)=x^<2>\) не достигает на интервале (0,1) своей точной нижней грани, равной нулю, и точной верхней грани, равной единице.
Промежуточные значения.
(теорема Коши о нулях непрерывной функции)
Если функция \(f\) непрерывна на отрезке [a,b] и принимает в его концах значения разных знаков, то есть \(f(a)f(b)\; Доказательство
\(\circ\) Разделим отрезок \([a,b]\) пополам. Пусть \(d\) — середина этого отрезка. Если \(f(d)=0\), то теорема доказана, а если \(f(d)\neq 0\), то в концах одного из отрезков \([a,d],\ [d,b]\) функция \(f\) принимает значения разных знаков. Обозначим этот отрезок \(\Delta_<1>=[a_<1>,b_<1>]\). Пусть \(d_<1>\) — середина отрезка \(\Delta_1\). Возможны два случая:
Продолжая эти рассуждения, получим:
С другой стороны, из неравенства \eqref
$$
\exists n_0\in\mathbb
Теорема 5 утверждает, что график функции \(y=f(x)\), непрерывной на отрезке \([a,b]\) и принимающей в его концах значения разных знаков, пересекает ось \(Ox\) (рис. 11.2) хотя бы в одной точке отрезка \([a,b]\).
Рис. 11.2
(теорема Коши о промежуточных значениях)
Если функция \(f\) непрерывна на отрезке \([a,b]\) и \(f(a)\neq (b)\), то для каждого значения \(C\), заключенного между \(f(a)\) и \(f(b)\), найдется точка \(\xi\in [a,b]\) такая, что \(f(\xi)=C\).
\(\circ\) Обозначим \(f(a)=A,\ f(b)=B\). По условию \(А\neq В\). Пусть, например, \(A 0\) и по теореме 5 найдется точка \(\xi\in [a,b]\) такая, что \(\varpi(\xi)=0\), то есть \(f(\xi)=C\). Утверждение \eqref
Если функция \(f\) непрерывна на отрезке \([a,b],\ m=\displaystyle \inf_
\(\circ\) Для всех \(x\in[a,b]\) выполняется неравенство \(m\leq f(x)\leq M\), причем согласно теореме 4 функция \(f\) принимает на отрезке \([a,b]\) значения, равные \(m\) и \(М\). Все значения из отрезка \([m,M]\) функция принимает по теореме 6. Отрезок \([m,M]\) вырождается в точку, если \(f(x)=const\) на отрезке \([a,b]\). \(\bullet\)
Существование и непрерывность функции, обратной для непрерывной и строго монотонной функции.
Ранее мы уже рассматривали понятие обратной функции. Докажем теорему о существовании и непрерывности обратной функции.
Если функция \(y=f(x)\) непрерывна и строго возрастает на отрезке \([a,b]\), то на отрезке \([f(a),(b)]\) определена функция \(x=g(y)\), обратная к f, непрерывная и строго возрастающая.
\(\circ\) Существование обратной функции. Обозначим \(A=f(a),\;B=f(b)\). Так как f — возрастающая функция, то для всех \(х\in [a,b]\) выполняется неравенство \(A\leq f(x)\leq B\), где \(A= \displaystyle \inf_
Согласно определению обратной функции (\S\ 9,п. 9) нужно доказать, что для каждого \(у_0\in [A,В]\) уравнение
$$
f(x)=y_<0>\label
$$
имеет единственный корень \(x=x_<0>\), причем \(x_0\in [a,b]\).
Существование хотя бы одного корня уравнения \eqref
Предположим, что наряду с корнем \(x=x_<0>\) уравнение \eqref
Пусть, например, \(\widetilde
$$
g(f(x))=x,\quad x\in[a,b],\quad f(g(y))=y,\quad u\in [A,B].\label
$$
Монотонность обратной функции. Докажем, что \(g(y)\) — строго возрастающая на отрезке [A,В] функция, то есть
$$
\forall\;y_<1>,\;y_<2>\in [A,B]:\quad y_<1>\; Замечание 6
Если функция \(f\) непрерывна и строго убывает на отрезке \([a,b]\), то обратная к ней функция \(g\) непрерывна и строго убывает на отрезке \([f(b),f(a)]\).
Аналогично формулируется и доказывается теорема о функции \(g\), обратной к функции \(f\), для случаев, когда функция \(f\) задана на интервале (конечном либо бесконечном) и полуинтервале.
Если функция \(f\) определена, строго возрастает и непрерывна на интервале \((a,b)\), то обратная функция \(g\) определена, строго возрастает и непрерывна на интервале \((A,B)\), где
$$
A=\lim_
$$
Непрерывность функций с примерами решения и образцами выполнения
Непрерывность функции:
Непрерывные функции, точки разрыва и их классификация, действия над непрерывными функциями, свойства функций, непрерывных на сегменте.
Определение:
Функция у = f(x) называется непрерывной в точке х₀, если:
Если в точке x₀ функция непрерывна, то точка x₀ называется точкой непрерывности функции.
Пример:
Исследовать на непрерывность функцию 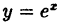
Решение:
Чтобы доказать, что функция 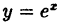
Таким образом, доказано, что функция 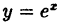
Замечание:
Формулу (10.1) можно записать в виде
(10.2)
так как 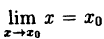
Введем понятие непрерывности функции в точке х₀ справа и слева.
Если, существует 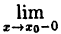
Так как ∆x = x-x₀, a ∆y = f(x)-(x₀), то условие (10.1) равносильно следующему:
Определение:
Функция у = f(x) называется непрерывной в точке х₀, если бесконечно малому приращению аргумента соответствует бесконечно малое приращение функции
(10.3)
Пример:
Показать, что функция у = х³ непрерывна для любого значения аргумента х.
Решение:
Найдем приращение функции ∆y.
Используя теоремы о пределе суммы и произведения функции, получим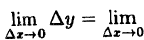
Следовательно, функция у = х³ непрерывна при — ∞ Точки разрыва функции и их классификация
Определение:
Точка х₀ называется точкой разрыва функции у = f(x), если она принадлежит области определения функции или ее границе и не является точкой непрерывности.
Так, например, функция 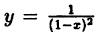
Определение:
Точка разрыва x₀ функции у = f(x) называется точкой устранимого разрыва, если существуют оба односторонних предела в точке x₀ и они равны, т. е.
Пример:
Исследовать на непрерывность функцию
Решение:
В точке x=-1 функция не определена, так как, выполнив подстановку, получаем неопределенность 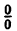
Определение:
Если в точке x₀ односторонние пределы слева и справа существуют, но не равны, точка x₀ называется точкой разрыва I рода.
Пример:
Исследовать на непрерывность функцию
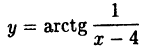
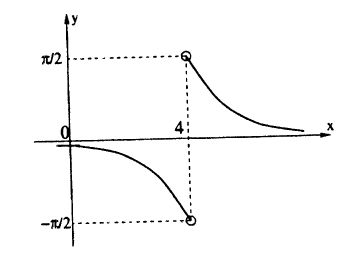
Решение: Вычислим односторонние пределы функции в точке ее разрыва х = 4.
Предел слева —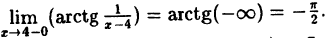
Предел справа — 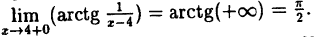
Пределы слева и справа существуют, но не равны, следовательно, точка x = 4 для данной функции — точка разрыва I рода (точка скачка).
Определение:
Точки разрыва, не являющиеся точками разрыва I рода, называются точками разрыва II рода.
В точках разрыва II рода не существует хотя бы один из односторонних пределов. Функция 
Действия над непрерывными функциями
Теорема:
Непрерывность суммы, произведения и частного непрерывных функций. Если функции ϕ(x) и ψ(x) непрерывны в точке Хо, то их сумма и произведение также непрерывны в точке x₀. Если, кроме того, знаменатель в рассматриваемой точке не равен нулю, то частное непрерывных функций есть функция непрерывная.
Докажем непрерывность произведения.
Дано: непрерывность функций в точке x₀:
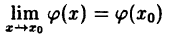
Доказать, что f(x) — ϕ(x) ∙ ψ(x) есть функция непрерывная в точке x₀, т. е. 
Доказательство:




Можно строго доказать, что все основные элементарные функции непрерывны при всех значениях х, для которых они определены.
Например, степенная у = xⁿ, показательная у = 
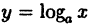
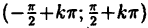
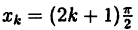
Теорема:
Непрерывность сложной функции. Если функция и = ϕ(x) непрерывна в точке x₀, а функция у = f(u) непрерывна в точке и₀ = ϕ(x₀), то сложная функция у = f [ϕ(x)] непрерывна в точке x₀.
В заключение этого раздела рассмотрим два предела, которые нам понадобятся в дальнейшем.
Пример:
Вычислить
Решение:
Заметим, что при х → 0 числитель и знаменатель одновременно стремятся к нулю, т.е. имеет место неопределенность вида 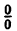
Так как данная логарифмическая функция непрерывна в окрестности точки х = 0, то можно перейти к пределу под знаком функции ( 

но 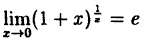
Следовательно,
(10.4)
В частности, при а = е
(10.5)
Таким образом, у = ln( 1 + х) и у = х — эквивалентные бесконечно малые функции при х → 0.
Пример:
Вычислить
Решение:
Здесь мы имеем дело с неопределенностью вида 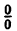
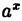
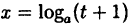
Так как на основании результата, полученного в предыдущем примере, 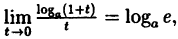
(10.6)
В частности, если а = е, имеем
т.е. у = 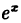
Свойства функций, непрерывных на сегменте
Определение:
Функция у = f(x) непрерывна на сегменте [а, b], если она непрерывна во всех внутренних точках Этого сегмента, а на концах сегмента (в точках a и b) непрерывна соответственно справа и слева.
Теорема:
Если функция у = f(x) непрерывна на сегменте [а, b], то она достигает на этом сегменте своего наибольшего и(или) наименьшего значения.
Простым доказательством этой теоремы, является геометрическая иллюстрация функции у = f(x) на рисунке 91. Непрерывная на сегменте [α, b] функция достигает наименьшего своего значения в точке х = x₁= а, а наибольшего значения в точке х₂.
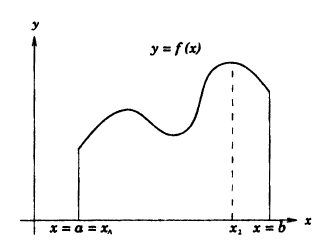
Следствие:
Если функция у = f(x) непрерывна на сегменте [a, b], то она ограничена на этом сегменте.
Действительно, если по теореме 10.3 функция достигает на сегменте наибольшего M и наименьшего т значений, то имеет место неравенство m ≤ f(x) ≤ M для всех значений функции на рассматриваемом сегменте. Т. е. |f(x)| ≤ M и, следовательно, функция у = f(x) ограничена на сегменте [а, b].
Теорема:
Теорема Больцано-Коши. Если функция у = f(x) непрерывна на сегменте [а, b] и на ее концах принимает значения разных знаков, то внутри этого сегмента найдется, по крайней мере, одна тонка С, в которой функция равна нулю.
Геометрический смысл теоремы заключается в следующем: если точки графика функции у = f(x), соответствующие концам сегмента [a, b], лежат по разные стороны от оси ОХ, то этот график хотя бы в одной точке сегмента пересекает ось OX. На данном рисунке 92 это три точки x₁, x₂, x₃.
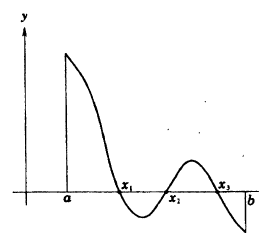
Теорема:
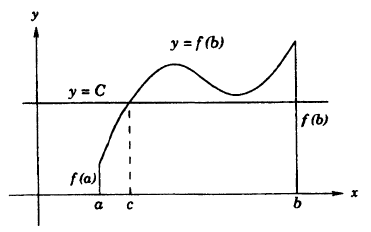
О промежуточных значениях функции. Если функция у = f(x) непрерывна на сегменте [α, b] и f(α) = A и f(b) = В, то для любого числа С, заключенного между A и B, найдется внутри этого сегмента такая точка с, что f(c) = С.
Из графика на рисунке 93 видно, что непрерывная функция, переходя от одного значения к другому, обязательно проходит через все промежуточные значения.
Теорема:
О непрерывности обратной функции.) Если функция у = f(x) непрерывна на сегменте [а, b] в возрастает (убывает) на этом сегменте, то обратная функция х = f⁻¹(y) на соответствующем сегменте оси OY существует и является также непрерывной возрастающей (убывающей) функцией.
Эту теорему мы принимаем без доказательства.
Решение на тему: Непрерывная функция
Пример:
Показать, что функция у = 4x² непрерывна в точке х = 2.
Решение:
Для этого необходимо показать, что в точке х = 2 выполняется все три условия непрерывности функции:
1) функция у = 4х² определена в точке х = 2 ⇒ f(2) = 16;
2) существует 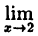
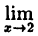
3) этот предел равен значению функции в точке х = 2
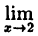
Пример:
Показать, что функция у = sin x непрерывна для любого значения аргумента х.
Решение:
Найдем приращение функции ∆y, используя формулы тригонометрических тождеств
Так как 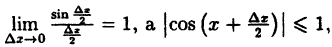
Эта функция (рис. 94) определена во всех точках сегмента [0,4] и ее значение при х = 3 ⇒ у = 2. Функция терпит разрыв, так как она не имеет предела при х → 3 :
Следовательно, точка х = 3, точка разрыва первого рода. При этом в граничных точках исследуемого сегмента [0,4], функция f(x) непрерывна справа (х = 0) и непрерывна слева (х = 4).
Пример:
Исследовать на непрерывность функцию
Решение:
В точке х = 5 функция не определена, т.к., выполнив подстановку, получаем неопределенность вида 0/0. Легко доказать, что
Следовательно, точка х = 5 точка устранимого разрыва.
Пример:
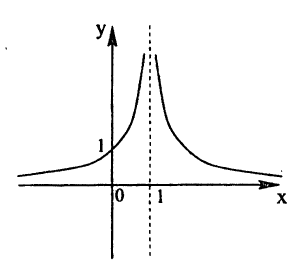
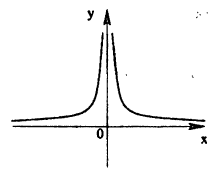
Исследовать на непрерывность функцию
Решение:
В точке х = 0 функция (рис. 95) терпит разрыв, так как она не определена в этой точке. Пределы функции слева и справа от точки х = 0 равны ∞. Следовательно, точка х = 0 для данной функции является точкой разрыва второго
Пример:
Исследовать на непрерывность функцию
Решение:
В точке х = 0 функция терпит разрыв 1-го рода, так как односторонние пределы существуют в этой точке, но не равны:
предел слева
предел справа
Пример:
Исследовать на непрерывность функцию 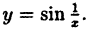
Решение:
Пример:
Исследовать на непрерывность функцию
Решение:
Функция 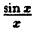
Если доопределить функцию 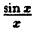
f(х) =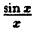
Доопределив функцию в точке х = 0, мы устранили разрыв.
Непрерывность функций



Решение заданий и задач по предметам:
Дополнительные лекции по высшей математике:
Образовательный сайт для студентов и школьников
Копирование материалов сайта возможно только с указанием активной ссылки «www.lfirmal.com» в качестве источника.
© Фирмаль Людмила Анатольевна — официальный сайт преподавателя математического факультета Дальневосточного государственного физико-технического института