Геоид и эллипсоид в чем разница
Геоид и эллипсоид в чем разница
Установить точное положение геоида под материками невероятно сложно, так как для математического выражения геоида используются коэффициенты сферических гармоник. Например, некоторые геоиды использует коэффициенты сферических гармоник для полиномов до 360 порядка и для полного уравнения требуется более 60 000 коэффициентов. Для расчета поверхности это все слишком сложно. Поэтому используется более простая фигура, но с достаточной точностью описывающая землю.
Для упрощения математических расчетов используется более удобный двухосный эллипсоид вращения, при этом он не сильно отличается от формы земли. Поверхности эллипсоида и геоида отличаются в пределах 100 метров в ту или иную сторону.
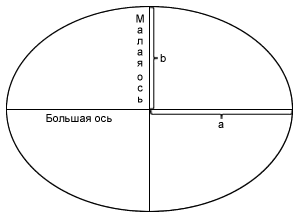
Форма эллипса определяется двумя радиусами. Более длинный радиус называется большой полуосью (как правило обозначается буквой a), а меньший (короткий)- малой полуосью (как правило обозначается буквой b).
Рисунок 26. Эллипсоид
Эллипсоид вращения, который наилучшим образом согласуется с поверхностью геоида называют общеземной эллипсоид или эллипсоид земли.
Эллипсоид, который наилучшим образом согласуется с геоидом на ограниченной части его поверхности называется референц-эллипсоид (от лат. referens – вспомогательный).
Эллипсоид вращения может быть определен либо большой полуосью, a, и малой полуосью, b, либо величиной a и сжатием.
Сжатие разность в длине между двумя осями, выраженная простой или десятичной дробью:
Сжатие является маленькой величиной, поэтому как правило вместо него используется величина 1/f.
Далее представлены некоторые референц-эллипсоиды и их параметры:
Помимо эллипсоида в геодезии используется такое понятие как датум. Датум (лат. Datum) — набор параметров, используемых для смещения и трансформации референц-эллипсоида в локальные географические координаты. Понятие датум используется в геодезии и картографии для наилучшей аппроксимации к геоиду в данном месте.
Датум задается смещением референц-эллипсоида по осям: X, Y, Z, а также поворотом декартовой системы координат в плоскости осей на угол rX, rY, rZ. Также необходимо знать параметры референц-эллипсоида а и f, где а — размер большой полуоси, f — сжатие эллипсоида.
Существуют два типа датумов- геоцентрический (глобальный) и локальный. Геоцентрический датум использует центр масс земли в качестве начала отсчета. Начало отсчета системы координат для локального датума сдвинуто относительно центра земли. Локальный датум изменяет положение эллипсоида так, чтобы наиболее близко совместить его поверхность с нужной областью. Локальный датум не следует применять вне области, для которой он был разработан.
Наиболее широко используемым датумом является Мировая геодезическая система 1984 года (World Geodetic System 1984- WGS84), базируется он на эллипсоиде WGS-84 с центром в центре масс земли. Так же один из достаточно распространенных датумов (используется в России и некоторых окружающих странах) является- Pulkovo-1942 (СК-42), который базируется на эллипсоиде Крассовского, начало координат у него смещено относительно центра масс расстояние около 100 м.
Система WGS-84 широко применяется за рубежом, ее используют практически для всех данных производимых в мире, так же она используется практически во всех навигаторах. СК-42 широко используется в российской картографии, на ней основываются все топографические материалы ВТУ ГШ РФ (Военно-топографического управления Генерального штаба Российской Федерации).
Далее представлены некоторые датумы:
Поддерживаемые ZuluGIS датумы приведены в приложении: Таблица 16, «Датумы».
Форма Земли, или что такое геоид
Всем привет. Из дискуссий о форме Земли я часто замечаю, что люди знают слово геоид, но зачастую не представляют, что именно это слово означает. Хочу тезисно осветить тему.
В последующие века геодезия (наука о фигуре Земли) продолжала развиваться, а с появлением космических аппаратов в 20 веке появилась и спутниковая геодезия, с помощью которой удалось дополнительно уточнить параметры фигуры Земли.
В качестве системы описания параметров Земли используется WGS 84 или её российский аналог ПЗ-90. В качестве отсчётного тела используется общеземной эллипсоид вращения с большой полуосью (то есть средним экваториальным радиусом) 6378 км и сжатием эллипсоида 1/298. [3]
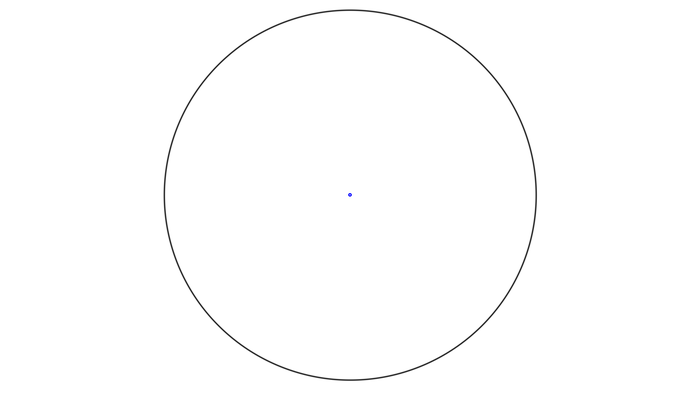
Например сверху Северный полюс, снизу Южный, вращаем этот эллипс вокруг оси, проходящей через полюса, и получаем общеземной эллипсоид вращения. Внимание, вопрос: видите ли вы отличие этого эллипса от окружности? Вряд ли. Поэтому если вы упоминаете сплюснутость Земли сами или слышите о сплюснутости от другого человека, вспоминайте эту картинку.
В некоторых сетевых дискуссиях люди меня уверяли, что если фигура хоть сколько-то отличается от шара, то это уже не шар. Вот такая, понимаете ли, принципиальность. Мои попытки рассказать этим людям, что идеальных геометрических фигур в физической реальности не существует, были не очень успешны. И когда я демонстрировал вышеприведённую картинку и спрашивал, чем же она так отличается от окружности, мне либо говорили, что я рисую вообще что-то не то, либо разводили руками.
Из вышесказанного вы уже понимаете, что вторым приближением к форме Земли является общеземной эллипсоид вращения (с вышеуказанными величинами большой полуоси и сжатия). Если представить себе Землю без суши, с ровным дном и без неоднородных вкраплений (плотные породы и тому подобное), то форма Земли (а именно поверхность мирового океана) с хорошей точностью совпадала бы с эллипсоидом вращения.
К слову, эллипсоид вращения и образовался как раз из-за суточного вращения нашей планеты, и когда возникает вопрос «почему нет горба воды в районе экватора из-за вращения», я отвечаю, что «горб» как раз есть, но он размазан между экватором и полюсом. Сумма гравитационной и центробежной сил как раз и дают направление силы тяжести (локальной вертикали), которая практически перпендикулярна к нашему эллипсоиду.
Практически перпендикулярна, однако в следующем, третьем приближении, есть отклонения направления силы тяжести (называется уклонением отвеса), связанные с неоднородностями: неровная поверхность суши и дна водоёмов, а также неравномерное распределение плотностей во внутренней структуре Земли. Это приводит к тому, что реальная поверхность мирового океана отличается от эллипсоида на величины до 100 метров. Такая уровенная поверхность невозмущённой поверхности мирового океана, причём продолженная под континентами, и называется геоидом. [4]
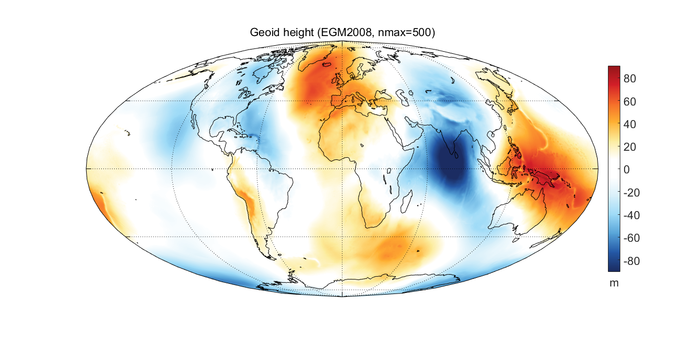
Так выглядит карта высот геоида относительно эллипсоида:
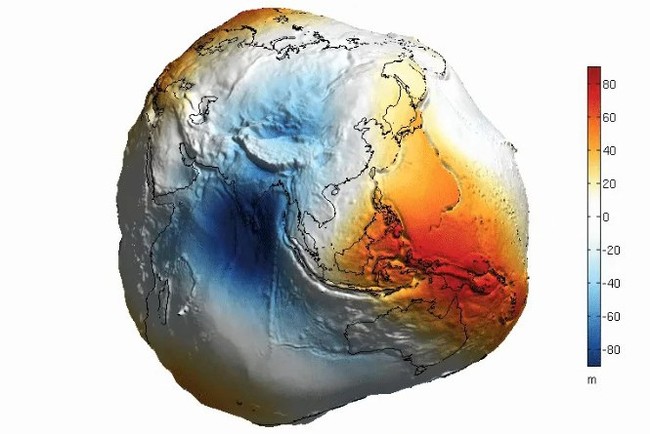
Понятно, что если на глаз трудно отличить даже 20-километровую сплюснутость Земли (эллипсоид в сравнении с шаром), то отличия геоида от эллипсоида в десятки метров в масштабе были бы тем более незаметны. Поэтому для целей визуализации отличий геоида от эллипсоида (не от шара, подчёркиваю) была сделана картинка, в которой эти отличия были утрированы на несколько порядков. А затем эту картинку кто-то вбросил со словами «так выглядит Земля без воды!» И почему-то этот вброс в своё время приобрёл вирусный характер, и до сих пор многие так и продолжают считать, что это форма Земли без воды:
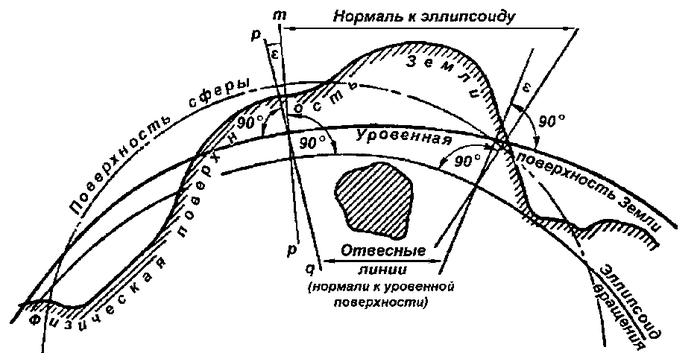
Ну и завершим мы такой, например, вполне подходящей картинкой, на которой не в масштабе, а условно приведены разные поверхности всех трёх приближений к форме Земли (сфера, эллипсоид вращения, геоид):
[1] Эти измерения проводили с помощью триангуляционной разметки на Земле и последующих астрономических измерений высоты кульминации выбранной звезды.
[3] Приведённые значения округлены, более точные значения составляют 6378136 метров и 1/298.258.
9. Какую форму имеет Земля?
Из книги «Восприятие и познание мира» З.С. Беловой:
(стр. 35) «Безусловно, целостная картина мира в сознании человека – это продукт эволюции, она меняется в разных культурах, в разные исторические эпохи. В этой связи особый познавательный интерес вызывает история становления представления людей о форме Земли.
Земля представлена была как плоский круг, обращённый лицом к зрителю. …Пытаясь убеждать и других, астрономы усовершенствовали эту модель. Теперь Земля представляла как выкуплый диск, лежащий на спине слона, который стоит на спине черепахи, а последняя плавает, в свою очередь, в безбрежном океане».
Думаю, данное видение было взято из мифологии и не правильно истолковано. Безбрежный океан – это космическое пространство, то есть не пустота. Выпуклый диск – это сфера. Слон – это основа, а именно ось вращения Земли. Черепаха имеет выпуклый панцирь, то есть положение слона (оси Земли) на ней устойчивое только в определённой точке. Так я мыслю скрытый смысл мифа. Конечно, он основан на тех знаниях, что я имею.
«На протяжении тысячелетий считалось очевидной истинной, что Земля плоская. Думать иначе казалось абсурдом. Но древнегреческий мыслитель Пифагор пришёл к выводу, что Земля имеет форму шара. Вероятно, этот вывод имел под собой эмпирическую базу, но аргументация, приведённая самим Пифагором, вытекала из идеи совершенства и гармонии мира, столь важной для мировоззрения. Воплощением гармонии формы является сфера, потому, по убеждению, Пифагора, Земля должна иметь сферическую форму.
Дальнейшее развитие концепции шарообразности Земли было осуществлено в IV веке до н.э. крупным учёным Древней Греции Аристотелем. Он указал на то, что при приближении к высоким объектам первоначально появляются из-за горизонта их верхние, а затем уже нижние части, а также на то, что при передвижении на север или на юг высота Полярной звезды над горизонтом изменяется. Эти явления, конечно же, свидетельствовали о кривизне земной поверхности и вполне согласовывались с предположением, что Земля – это шар, но ещё не доказывали его.
По мере углубления познания гипотеза о форме Земли уточняется, конкретизируется по схеме, близкой к логике восхождения от абстрактного к конкретному. История развития этой гипотезы показала, что первоначальная умозрительная идея является своего рода абстракцией, но такой, которая выполняет роль модельного представления реальности».
Получается, что окружающий мир, тот, который мы видим и ощущаем, существует только в нашем сознании и изменяется по мере его развития. Так ли это? А как же прошлое и будущее? Для нас существует только настоящее. Оно и влияет на наши представления о прошлом и будущем.
«На следующем этапе развития гипотезы Земля была представлена как эллипсоид вращения, то есть как тело, которое образуется от вращения эллипса вокруг его малой оси. Известно, что тело тем больше сплющено, чем быстрее совершается его вращение вокруг собственной оси. Предполагалось, что тело, переставшее вращаться снова примет форму шара».
Значит ли это, что изменчива сама форма Земли или же изменчивы наши представления об этой форме?
«В связи с этим выяснилось, что форма Земли явно отклоняется от правильного шара: во-первых, благодаря вращению вокруг своей оси приобрела форму эллипсоида, во-вторых, эллипсоид утончается в форме геоида.
Фигура Земли, построенная только по зональным характеристикам, имеет грушевидную форму, вытянутую к северу и сплюснутую с юга. Таким образом, Земля обладает ещё одной чётко выраженной формой – грушевидностью».
Неудивительно, так как один полюс Земли повёрнут к Солнцу.
«Шар, эллипсоид, геоид, грушевидность – суть различных гипотез. Они или исключают, или дополняют друг друга. Ответить на вопрос, какова же форма Земли, могли учёные не столько простыми умозаключениями, сколько измерениями, наблюдениями, экспериментом.
Карта Земли при некотором преувеличении должна выглядеть как эллипс. Считать Землю эллипсом удобно, ибо это – простая геометрическая поверхность и её легко отобразить на картах. Эллипсоид описывается простыми формулами геометрии и на его поверхности нетрудно решать различные геодезические задачи. Самые большие отклонения реальной физической поверхности Земли от хорошо подобранного эллипсоида не превышают восемь – девять километров (пики высочайших вершин), в среднем же они не больше сотен метров на континентах и десятков метров на океанах.
Эти данные требовали некоторой идеализации формы Земли. Практические данные показали, что Земля – геоид, который определяется как средняя поверхность моря.
Чтобы понять, как выглядит поверхность геоида на материках, надо вообразить себе, что через материки прорыты каналы, и вода в них стоит на уровне моря. Форма геоида зависит также от гравитационного притяжения Земли. О том, что ускорение свободного падения повсюду на Земле примерно одинаково, свидетельствует форма геоида и его почти гладкая поверхность.
В конце прошлого столетия было введено понятие геоида как геометрической фигуры, представляющей Землю. За геоид принимается уровень поверхности, которая совпадает с поверхностью воды в океанах, если отсутствуют волны, ветровой надув и прочие возмущающие явления. В районе континентов эта поверхность проходит под сушей. Вообще уровенной поверхностью называется поверхность равного потенциала силы тяжести (работы, совершаемой единичной массой при переносе её из безконечности в данную точку или на данную поверхность). Линии действия сил всегда перпендикулярны уровенной поверхности, и поэтому жидкость на ней находится в равновесии и не должна перетекать. Геоид как уровенная поверхность почти точно совпадает с поверхностью Земли на океанах и отклоняется от неё на континентах, и это отклонение тем больше, чем больше возвышается континент над уровнем моря. Учёные ввели понятие геоида как третье, более точное приближение к фигуре Земли по сравнению с шаром и эллипсоидом».
«Геоид – эквипотенциальная поверхность (геометрическое место точек равных потенциалов) земного поля тяжести, приблизительно совпадающая со средним уровнем вод Мирового океана в невозмущённом состоянии и условно продолженная под материками.
Геоид по форме больше похож на грушу, чем на шар. Форму геоида можно узнать только с помощью обширных гравитационных измерений и расчётов. Структура распределения тяготеющих масс Земли влияет на форму геоида. С геоидом связана система астрономических координат, с эллипсоидом вращения – система геодезических координат» (Википедия).
Получается, что геоид – это такая форма Земли, которая даст возможность понять, как Земля связана с окружающим её космическим пространством и с объектами, находящимися в нём.
В чём значение геоида для самой Земли, как её формы?
«Геоид является поверхностью, относительно которой ведётся отчёт высот над уровнем моря, в силу чего знание параметров геоида необходимо, в частности, в навигации – для определения высоты над уровнем моря на основе геодезической (эллипсоидной) высоты, измеряемой GPS – приёмниками, а также в физической океанологии – для определения высот морской поверхности.
Высота над уровнем моря – мнимая мера разности потенциалов в точке земной поверхности и в начале счёта высот. В исходном пункте высота принимается равной нулю.
Навигация – определение местоположения, скорости и ориентации движущихся объектов.
Уровень моря – положение свободной поверхности Мирового океана, измеряемое по отвесной линии относительно некоторого условного начала отсчёта.
Океанология или океанография изучает крупномасштабное взаимодействие океана и атмосферы и его длинноприродную изменчивость, химический обмен океана с материками, атмосферой и дном, биоту (исторически сложившаяся совокупность видов организмов) и её экологические взаимодействия.
Исследования с использование изменяющегося во времени геоида, рассчитанные по данным GRACE, позволили получить информацию о глобальных гидрологических циклах, балансах массы ледниковых щитов и гляциозостазии (очень медленные горизонтальные и вертикальные движения земной поверхности на территориях древнего и современного оледенения). Данные экспериментов GRACE также могут использоваться для определения вязкости мантии Земли» (Википедия).
Для чего это нужно человечеству? Для того, что понять механизм смены полюсов Земли, а, следовательно, суметь пережить очередной глобальный катаклизм. Из древних учений следует, что такие катаклизмы происходят примерно каждые 6000 лет, чередуясь огненным и водным.
«В отличие от эллипсоида, геоид ближе к реальной фигуре Земли и совпадает с ней. Теория геоида подтверждается эмпирическими следствиями. При геодезических измерениях горные породы, обладающие сравнительно большей массой, чем их окружающая среда, отклоняют отвес от центра Земли и притягивают к себе. При этом отвес отклоняется от расчётного направления на центр тяжести эллипсоида, совпадая с направлением на местный центр тяжести. Последнее перпендикулярно истинной горизонтальной плоскости, касательно к поверхности геоида, поэтому плоскость, касательная к поверхности эллипсоида, является мнимой.
Земля имеет слегка грушевидную форму, причём «черенок груши» располагается у северного полюса. Грушевидность частично объясняется существованием пары, расположенных в противоположных направлениях гравитационных «впадин» в северном и южном полушариях. Глубина этих впадин достигает семидесяти пяти метров».
Необходимо заметить, что изменения во взглядах на форму Земли происходили с усложнением самой формы, причём предыдущий взгляд становился часть последующего.
«Известно, что познающий субъект на каждом историческом отрезке развития общества ограничен в воспроизведении мира. Окружающий мир безконечен и никогда не может быть познан полностью».
То есть представление о форме Земли будет развиваться и усложнятся и дальше, по мере эволюции самого человечества.
«Но важно и другое. Познавательный образ, воспринимаемый зрительно, в некотором роде богаче, чем объективная действительность и практика, в ходе которой он возникает.
Теория, как правило, развивается, уточняется, проходит через горнило острых противоречий дискуссий, тем самым она всё более приближается к истине. И в этих условиях она не должна покидать реалистическую почву, ибо из всех видов информации только логическая информация и связанные с ней принципы рационализма, как метода познания могут достаточно аргументировано претендовать не только на описание, но и логическое объяснение происходящего вокруг нас».
Влияние модели геоида при ГНСС-измерениях
Эллипсоид – это фигура с известными геометрическими свойствами, основными параметрами которой являются
a – большая полуось
b – малая полуось
α = (a-b)/a – полярное сжатие
Из-за сложной формы земной поверхности нельзя подобрать такую фигуру эллипсоида, которая одинаково хорошо подходила бы ко всем участкам Земли. Для минимизации ошибок локализации были введены различные референц-эллипсоиды для отдельных стран/континентов.
В России примером референц-эллипсоида является всем хорошо известный эллипсоид Красовского с параметрами по ГОСТ Р 51794-2008:
a = 6378245 м
α =1/298,3
Геоид – это уровенная (эквипотенциальная) поверхность, приблизительно совпадающая с уровнем мировых вод в невозмущенном состоянии, в каждой точке которой направление силы тяжести перпендикулярно. Поверхность геоида неравномерна и пересекается с поверхностью эллипсоида.
Самые популярные модели геоида – EGM96 и EGM2008, но на самом деле их гораздо больше.
Модели могут быть как глобальными, так и региональными или даже локальными, рассчитанными специально для вашей территории работ. Могут различаться по частоте шага сетки измерений, например, EGM2008 2,5′ или EGM2008 1′. Вторая, естественно, более точная, но и вес такой модели больше.
Посмотреть основные модели геоида, скачать, а также обрезать их под свой регион, чтобы уменьшить вес модели, можно на сайте:
http://icgem.gfz-potsdam.de/calcgrid
Также, обрезка глобальной модели геоида возможна в ПО Trimble TBC.
Модель геоида загружается либо в полевое ПО, либо в ПО для постобработки, а затем назначается для использования.
Высота геоида над эллипсоидом называется аномалией высоты. В зарубежных источниках или ПО также распространено понятие undulation, т.е. ондуляция. С точки зрения геодезии эти понятия являются синонимами, однако в других дисциплинах ондуляция может иметь иной смысл!
1. От референц-эллипсоида – эллипсоидальная (геодезическая) высота. Такую высоту мы получаем с помощью ГНСС-измерений, когда модель геоида не учитывается в расчетах.
2. От геоида – ортометрическая высота или высота над уровнем моря.
2.1 От квазигеоида по нормали – нормальная (нивелирная) высота. Нормальную высоту мы получаем с помощью любого прибора, связанного с гравиметрическими измерениями на поверхности Земли. Это может быть нивелир, теодолит или тахеометр – горизонтируя прибор с помощью уровня, мы устанавливаем его в соответствии с направлением силы тяжести – по нормали.
Если необходимо увязать спутниковые измерения с измерениями на основе силы тяжести, то используем модель геоида
При ГНСС-измерениях превышения рассчитываются математически по эллипсоиду.
Применяя в расчете модель геоида, мы можем привести эллипсоидальную высоту к нормальной благодаря значениям ондуляции.
Если нам необходимо перейти к Балтийской системе высот или любой другой системе высот, основанной на нивелирных измерениях, то используем модель геоида + калибровку на местности.
Можно обойтись только калибровкой в том случае, если участок работ небольшой (несколько десятков км), а аномальные зоны на нем исключены. К аномальным зонам можно отнести горы, плотности и пустоты в земле, неоднородности земной коры, нефтяные и газовые моря.
Например, при вычислении объемов тел нет такой необходимости, потому что измерения относительные
В заключение хочется сказать, что применение или неприменение модели геоида всегда зависит от ваших задач. Хорошо обдумайте ее, а затем принимайте решение. Главное, следите за тем, чтобы во время работы (в одном проекте) не произошло переключения между ортометрической и эллипсоидальной высотой!
Что касается терминов, то споры о них до сих пор ведутся как внутри российской школы гравиметрии, так и в сравнении с зарубежной. Поэтому зачастую в теории высот могут быть расхождения в разных источниках.