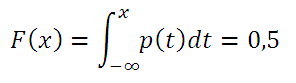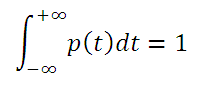Что возвращает функция медиана
Функция МЕДИАНА
В этой статье описаны синтаксис формулы и использование функции МЕДИАНА в Microsoft Excel.
Описание
Возвращает медиану заданных чисел. Медиана — это число, которое является серединой множества чисел.
Синтаксис
Аргументы функции МЕДИАНА описаны ниже.
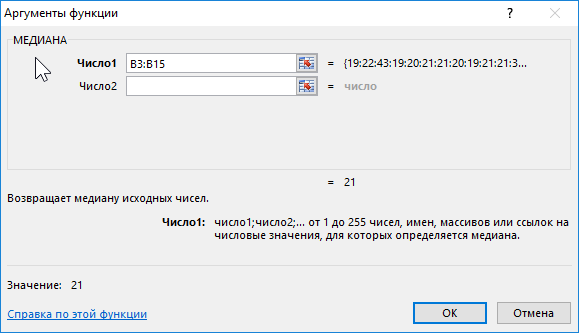
Число1, число2. Аргумент «число1» является обязательным, последующие числа необязательные. От 1 до 255 чисел, для которых требуется определить медиану.
Замечания
Если в наборе имеется ряду чисел, медиана вычисляет среднее значение двух чисел в середине. См. вторую формулу в примере.
Аргументы могут быть либо числами, либо содержащими числа именами, массивами или ссылками.
Учитываются логические значения и текстовые представления чисел, которые непосредственно введены в список аргументов.
Если аргумент, который является массивом или ссылкой, содержит текст, логические значения или пустые ячейки, то такие значения пропускаются; однако ячейки, которые содержат нулевые значения, учитываются.
Аргументы, которые являются значениями ошибки или текстами, не преобразуемыми в числа, приводят в возникновению ошибок.
Примечание: Функция МЕДИАНА измеряет центральную тенденцию, которая является центром множества чисел в статистическом распределении. Существует три наиболее распространенных способа определения центральной тенденции:
Среднее значение — это среднее арифметическое, которое вычисляется путем сложения набора чисел с последующим делением полученной суммы на их количество. Например, средним значением для чисел 2, 3, 3, 5, 7 и 10 будет 5, которое является результатом деления их суммы, равной 30, на их количество, равное 6.
Медиана — это число, которое является серединой множества чисел, то есть половина чисел имеют значения большие, чем медиана, а половина чисел имеют значения меньшие, чем медиана. Например, медианой для чисел 2, 3, 3, 5, 7 и 10 будет 4.
Мода — это число, наиболее часто встречающееся в данном наборе чисел. Например, модой для чисел 2, 3, 3, 5, 7 и 10 будет 3.
При симметричном распределении множества чисел все три значения центральной тенденции будут совпадать. При смещенном распределении множества чисел значения могут быть разными.
Пример
Скопируйте образец данных из следующей таблицы и вставьте их в ячейку A1 нового листа Excel. Чтобы отобразить результаты формул, выделите их и нажмите клавишу F2, а затем — клавишу ВВОД. При необходимости измените ширину столбцов, чтобы видеть все данные.
Расчет медианой группы чисел
Предположим, что вы хотите узнать, что такое средний балл в распределении о оценкам учащихся или в образце данных для контроля качества. Чтобы вычислить медиану группы чисел, используйте функцию МЕДИАНА.
Функция МЕДИАНА измеряет центральную тенденцию, которая является центром множества чисел в статистическом распределении. Существует три наиболее распространенных способа определения центральной тенденции:
Среднее значение — это среднее арифметическое, которое вычисляется путем сложения набора чисел с последующим делением полученной суммы на их количество. Например, средним значением для чисел 2, 3, 3, 5, 7 и 10 будет 5, которое является результатом деления их суммы, равной 30, на их количество, равное 6.
Медиана — это число, которое является серединой множества чисел, то есть половина чисел имеют значения большие, чем медиана, а половина чисел имеют значения меньшие, чем медиана. Например, медианой для чисел 2, 3, 3, 5, 7 и 10 будет 4.
Мода — это число, наиболее часто встречающееся в данном наборе чисел. Например, модой для чисел 2, 3, 3, 5, 7 и 10 будет 3.
При симметричном распределении множества чисел все три значения центральной тенденции будут совпадать. При смещенном распределении множества чисел значения могут быть разными.
Снимки экрана в этой статье получены в Excel 2016. Если вы используете другую версию, интерфейс может немного отличаться, но функции будут такими же.
Пример
Чтобы этот пример проще было понять, скопируйте его на пустой лист.
Откройте пустую книгу или лист.
Выберите пример ниже.
Примечание: Не выделяйте заголовки строк или столбцов.
Функция МЕДИАНА
В этой статье описаны синтаксис формулы и использование функции МЕДИАНА в Microsoft Excel.
Описание
Возвращает медиану заданных чисел. Медиана — это число, которое является серединой множества чисел.
Синтаксис
Аргументы функции МЕДИАНА описаны ниже.
Число1, число2. Аргумент «число1» является обязательным, последующие числа необязательные. От 1 до 255 чисел, для которых требуется определить медиану.
Замечания
Если в наборе имеется ряду чисел, медиана вычисляет среднее значение двух чисел в середине. См. вторую формулу в примере.
Аргументы могут быть либо числами, либо содержащими числа именами, массивами или ссылками.
Учитываются логические значения и текстовые представления чисел, которые непосредственно введены в список аргументов.
Если аргумент, который является массивом или ссылкой, содержит текст, логические значения или пустые ячейки, то такие значения пропускаются; однако ячейки, которые содержат нулевые значения, учитываются.
Аргументы, которые являются значениями ошибки или текстами, не преобразуемыми в числа, приводят в возникновению ошибок.
Примечание: Функция МЕДИАНА измеряет центральную тенденцию, которая является центром множества чисел в статистическом распределении. Существует три наиболее распространенных способа определения центральной тенденции:
Среднее значение — это среднее арифметическое, которое вычисляется путем сложения набора чисел с последующим делением полученной суммы на их количество. Например, средним значением для чисел 2, 3, 3, 5, 7 и 10 будет 5, которое является результатом деления их суммы, равной 30, на их количество, равное 6.
Медиана — это число, которое является серединой множества чисел, то есть половина чисел имеют значения большие, чем медиана, а половина чисел имеют значения меньшие, чем медиана. Например, медианой для чисел 2, 3, 3, 5, 7 и 10 будет 4.
Мода — это число, наиболее часто встречающееся в данном наборе чисел. Например, модой для чисел 2, 3, 3, 5, 7 и 10 будет 3.
При симметричном распределении множества чисел все три значения центральной тенденции будут совпадать. При смещенном распределении множества чисел значения могут быть разными.
Пример
Скопируйте образец данных из следующей таблицы и вставьте их в ячейку A1 нового листа Excel. Чтобы отобразить результаты формул, выделите их и нажмите клавишу F2, а затем — клавишу ВВОД. При необходимости измените ширину столбцов, чтобы видеть все данные.
Медиана в EXCEL
history 23 октября 2016 г.
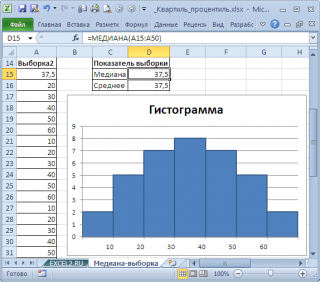
Начнем с медианы для выборок (т.е. для фиксированного набора значений).
Медиана выборки
Для вычисления медианы необходимо сначала отсортировать множество чисел (значения в выборке ). Например, медианой для выборки (2; 3; 3; 4 ; 5; 7; 10) будет 4. Т.к. всего в выборке 7 значений, три из них меньше, чем 4 (т.е. 2; 3; 3), а три значения больше (т.е. 5; 7; 10).
Если множество содержит четное количество чисел, то вычисляется среднее для двух чисел, находящихся в середине множества. Например, медианой для выборки (2; 3; 3 ; 6 ; 7; 10) будет 4,5, т.к. (3+6)/2=4,5.
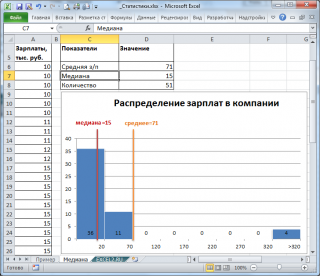
Очевидно, что средняя зарплата (71 тыс. руб.) не отражает тот факт, что 86% сотрудников получает не более 30 тыс. руб. (т.е. 86% сотрудников получает зарплату в более, чем в 2 раза меньше средней!). В то же время медиана (15 тыс. руб.) показывает, что как минимум у половины сотрудников зарплата меньше или равна 15 тыс. руб.
Медиана непрерывного распределения
Если Функция распределения F (х) случайной величины х непрерывна, то медиана является решением уравнения F(х) =0,5.
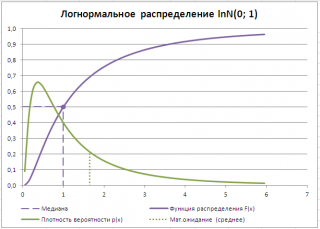
Например, решив аналитическим способом это уравнение для Логнормального распределения lnN(μ; σ 2 ), получим, что медиана вычисляется по формуле =EXP(μ). При μ=0, медиана равна 1.
Примечание : Напомним, что интеграл от функции плотности вероятности по всей области задания случайной величины равен единице.
Поэтому, линия медианы (х=Медиана) делит площадь под графиком функции плотности вероятности на две равные части.
Функция МЕДИАНА в Excel для выполнения статистического анализа
Функция МЕДИАНА в Excel используется для анализа диапазона числовых значений и возвращает число, которое является серединой исследуемого множества (медианой). То есть, данная функция условно разделяет множество чисел на два подмножества, первое из которых содержит числа меньше медианы, а второе – больше. Медиана является одним из нескольких методов определения центральной тенденции исследуемого диапазона.
Примеры использования функции МЕДИАНА в Excel
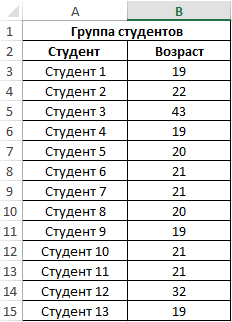
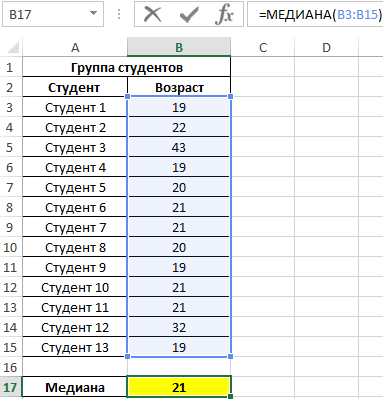
Пример 1. При исследовании возрастных групп студентов использовались данные случайно выбранной группы учащихся в ВУЗе. Задача – определить срединный возраст студентов.
Формула для расчета:
То есть в группе есть студенты, возраст которых меньше 21 года и больше этого значения.
Сравнение функций МЕДИАНА и СРЗНАЧ для вычисления среднего значения
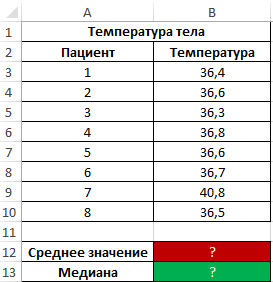
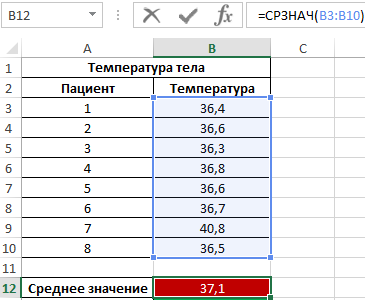
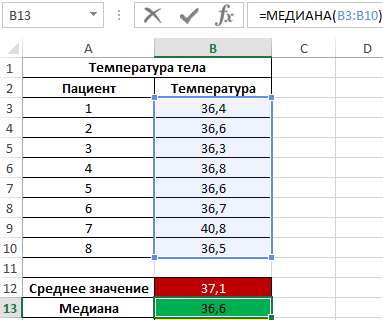
Пример 2. Во время вечернего обхода в больнице каждому больному была замерена температура тела. Продемонстрировать целесообразность использования параметра медиана вместо среднего значения для исследования ряда полученных значений.
Формула для нахождения среднего значения:
Формула для нахождения медианы:
Как видно из показателя среднего значения, в среднем температура у пациентов выше нормы, однако это не соответствует действительности. Медиана показывает, что как минимум у половины пациентов наблюдается нормальная температура тела, не превышающая показатель 36,6.
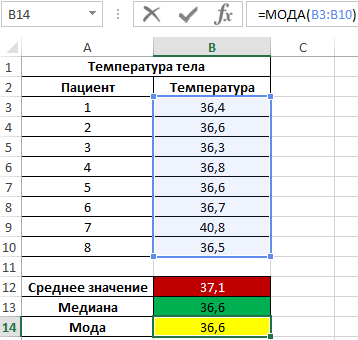
Внимание! Еще одним методом определения центральной тенденции является мода (наиболее часто встречающееся значение в исследуемом диапазоне). Чтобы определить центральную тенденцию в Excel следует использовать функцию МОДА. Обратите внимание: в данном примере значения медианы и моды совпадают:
То есть срединная величина, делящая одно множество на подмножества меньших и больших значений также является и наиболее часто встречающимся значением в множестве. Как видно, у большинства пациентов температура составляет 36,6.
Пример расчета медианы при статистическом анализе в Excel
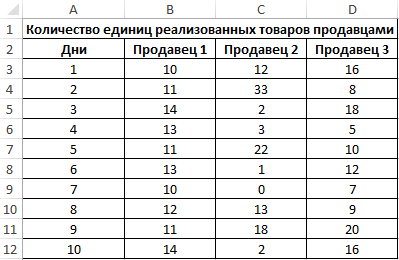
Пример 3. В магазине работают 3 продавца. По результатам последних 10 дней необходимо определить работника, которому будет выдана премия. При выборе лучшего работника учитывается степень эффективности его работы, а не число проданных товаров.
Исходная таблица данных:
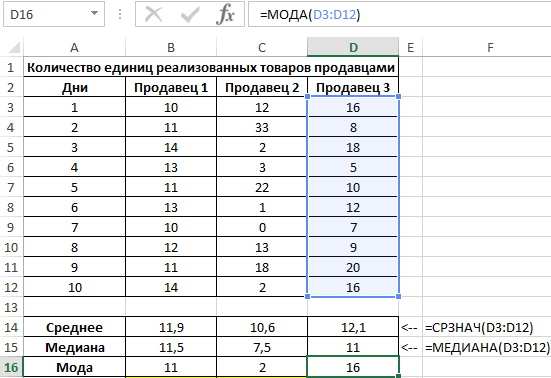
Для характеристики эффективности будем использовать сразу три показателя: среднее значение, медиана и мода. Определим их для каждого работника с использованием формул СРЗНАЧ, МЕДИАНА и МОДА соответственно:
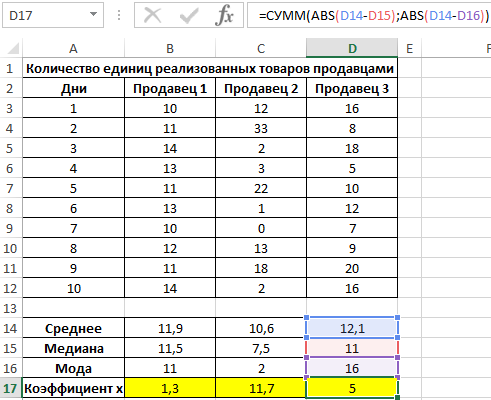
Для определения степени разброса данных используем величину, которая является суммарным значением модуля разницы среднего значения и моды, среднего значения и медианы соответственно. То есть коэффициент x=|av-med|+|av-mod|, где:
Рассчитаем значение коэффициента x для первого продавца:
Аналогично проведем расчеты для остальных продавцов. Полученные результаты:
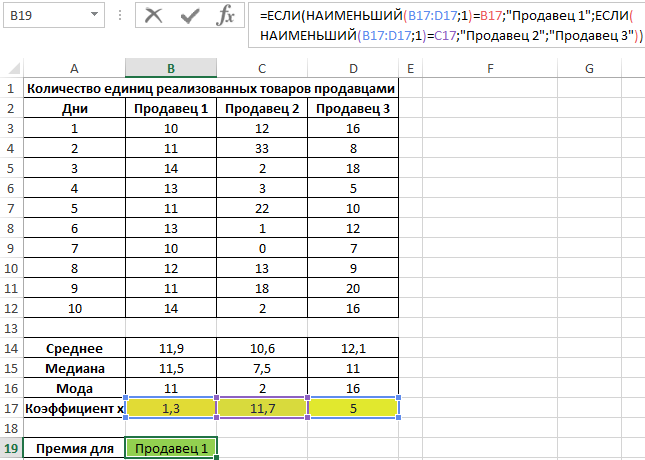
Определим продавца, которому будет выдана премия:
Примечание: функция НАИМЕНЬШИЙ возвращает первое минимальное значение из рассматриваемого диапазона значений коэффициента x.
Коэффициент x является некоторой количественной характеристикой стабильности работы продавцов, которую ввел экономист магазина. С его помощью удалось определить диапазон с наименьшими отклонениями значений. Этот способ демонстрирует, как можно использовать сразу три метода определения центральной тенденции для получения наиболее достоверных результатов.
Особенности использования функции МЕДИАНА в Excel
Функция имеет следующий синтаксис:
=МЕДИАНА( число1; [число2];. )