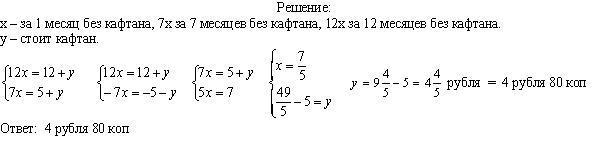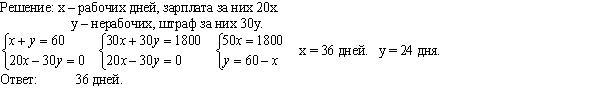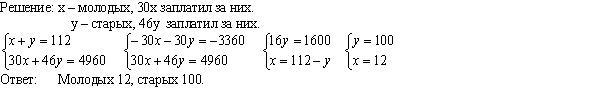Что восьмой взял у второго чтобы быть не хуже седьмого
Что восьмой взял у второго чтобы быть не хуже седьмого
вы знаете почему в июле и августе подряд по 31 дню, а в феврале максимум 29? день июль август февраль максимум
Император август указом положил для августа на один день больше, чтобы быть не хуже Юлия (июль) и отобрал этот день у февраля. Есть такая загадка: что восьмой взял у второго, чтобы быть не хуже седьмого)))
Июль назван честь Юлия Цезаря, а Август в честь его приемника Октавиана Августа, западло было месяцу, носящему имя императора быть коротким, вот и отняли у многострадального февраля тридцатый день
31 августа, что бы 1-*е сентября не резко наступало)))февраль, что бы 8е марта побыстрее настало))) в июле потому, что июнь короткий всего 30 для равномерности)))
Надя. мне вообще такой календарь не по душе..в своё время я разработал сввой..более удобный людям..но и только..он так и остался в проекте
самый капризный месяц и когда составляли календарь просто морозы сократили а солнечные дни продлили мысленно. это вариант фантазий.
лето продлить а зима что б по быстрей кончилась только не надо мне говарить что это в честь хороших и плохих провителей 
потому что не было императора по имени Февраль,который мог бы защитить свой месяц от посягательств Августа и Юлия
так решил император Август. Ему не понравилось, что у Юлия Цезаря ( в июле) 31 день, а в августе всего 30
Думаю связано с цикличностью природной, но можно конечно и просто порадоваться за школьников)
я сама иногда об этом задумываюсь. инитересно вообще, как составлялся теперешний календарь.
Император Август не хотел быть» ниже»императора Юлиана, и приказал сделать в августе 31 день
в августе из-за императора Августа ему обидно было, что в Июле 31 день, он от февраля и отнял
Где то читал но точно сейчас не помню но что то связано с обращением земли вокруг солнца
Где то читал но точно сейчас не помню но что то связано с обращением земли вокруг солнца
Где то читал но точно сейчас не помню но что то связано с обращением земли вокруг солнца
я была бы не против если бы летом было и по 40дней..а февралю и десятка бы хватило.)))
мат вертикаль, тестирование 7 кл
вот вам даже табличка. Вы просто не поняли сути и тупо считали в экселе. Должен быть именно расчет, чтобы суммы сошлись. Промежуточные, где они разнятся, не подходят. Это не жизненная задача, это школьная задача, и она должна решаться математически
Можно чуть проще увидеть
n это такое число, что нечётное количество месяцев, когда будет накоплена нужная сумма, представляется в виде 2n+1.
Авторы часто пренебрегают словами «минимальный» или подобными и тогда задача имеет несколько решений.
Да. у математиков да. Вы автор? Ваш ребенок прав. Доказать можно.
А авторам таких задач надо внимательно относиться к составлению.
Например, олимпиадные задачи (новые, не шаблонные) сначала составляют, потом обсуждают, исправляют и только потом предлагают для решения. Здесь пропущен этап обсуждения, состряпали и быстрее опубликовали.
Дали бы хотя бы ссылку где вы видите.
Я вот тут смотрю
https://clip2net.com/clip/m9117/116a8-clip-8kb.png?nocache=1
Надо получить 298. Это происходит на 9 месяце
А, дошло.
Из того, что цена вертолета неизвестна, вы предполагаете что он стоит не все деньги, которые есть у Вани в 6 месяцев, а лишь чуть больше, чем у него же было в 5.
Да, можно. Но только при таком подходе задача будет иметь множество решений, а это явно не предусматривалось составителями. Поэтому если не хочется с составителями долго бодаться, надо понять, что этот вариант тоже исключен.
Сказали бы давно, что предполагаете цену меньше, чем денег у Вани в 6 месяцев. Сколько человек не поняло ваше объяснение
Оно и в 9 месяцев точности так же всегда и ни от чего не зависит.
В 12 месяцев их деньги «всегда» равны, а в 9 месяцев денег у Дани «всегда» больше.
это если развернутое решение.
А если один ответ, то фиг что докажешь.
А если еще и поле для ввода единственного ответа, то правильный ответ вообще не введешь. Не говоря уже о том, что на обоснование этого длинного правильного ответа может уйти время на всю диагностику, и на остальные задания просто не хватит времени.
Копилка знаменитых задач продолжение 4
Внимание! Если вы увидите сообщение что количество опубликованных знаков превышает длину страницы, то вы можете разместить свои задачи на странице Копилка знаменитых задач продолжение 5
Содержание
Задачи участников ДООМ
Задача № 30. Крестьяне и картофель
Шли три крестьянина и зашли на постоялый двор отдохнуть и пообедать. Заказали хозяйке сварить картофель, а сами заснули. Хозяйка сварила картофель, но не стала будить постояльцев, а поставила миску с едою на стол и ушла. Проснулся один крестьянин, увидел картофель и, чтоб не будить товарищей, сосчитал картофель, съел свою долю и снова заснул. Вскоре проснулся другой; ему невдомек было, что один из товарищей уже съел свою долю, поэтому он сосчитал весь оставшийся картофель, съел третью часть и опять заснул. После чего проснулся третий; полагая, что он проснулся первым, он сосчитал оставшийся в чашке картофель и съел третью часть. Тут проснулись его товарищи и увидели, что в чашке осталось 8 картофелин. Тогда только объяснилось дело.
Сосчитайте, сколько картофелин подала на стол хозяйка, сколько съел уже и сколько должен еще съесть каждый, чтобы всем досталось поровну.
8*3/2=12- остаток после второго,
12*3/2=18- остаток после первого,
18*3/2=27- первоначальное число.
Каждый должен был съесть по 9 картофелин, первый съел свою долю, второму осталось съесть 3 картофелины, а третий должен съесть еще 5 картофелин.
—«Пифагор ID 220» 15:35, 27 октября 2008 (UZT)
Решение: За 24 подкованных гвоздя пришлось уплатить 1/4+1/2+1+2+2²+23+…+2(24-3) копеек. Сумма эта равна (2²∙2-1/4): (2-1) =2²²-1/4=4194303 ¾ коп., т.е. около 42 тысяч рублей. При таких условиях не обидно дать и лошадь в придачу.
Задача №3 Картина Богданова-Бельского «Трудная задача» известна многим, но мало кто из видевших эту картину вникал в содержание той «трудной задачи», которая на ней изображена. Состоит она в том, чтобы устным счетом быстро найти результат вычисления: (10²+11²2+12²+13²+14²):365
Решение: 10²+11²+12²=13²+14². Так как 100+121+144=365,то на картине выражение равно 2.
Задача 4. (из учебника «Введение в алгебру» Эйлера): Две крестьянки принесли на рынок вместе 100 яиц, одна больше, нежели другая; обе выручили одинаковые суммы. Первая сказала тогда второй: «Будь у меня твои яйца, я выручила бы 15 крейцеров». Вторая ответила: «А будь твои яйца у меня, я выручила бы за них 6 2/3 крейцера». Сколько яиц было у каждой?
Решение: У первой крестьянки было х яиц, у второй 100-х. Если бы первая имела 100-х яиц, она выручила бы, мы знаем 15 крейцеров. Значит, первая крестьянка продавала яйца по цене 15: (100-х) за штуку. Вторая крестьянка продавала яйца по цене 6 2/3 : х = 20: (3х) За штуку. Выручка первой крестьянки 15х: (100-х), второй 20(100-х): 3х. Так как выручки равны, то 15х: (100-х)= 20(100-х): 3х. После преобразования имеем: х²+160х-8000=0. Откуда х1=40, х2=-200.Отрицательный корень не имеет смысла; у задачи – только одно решение: Второй способ. Предположим, что вторая крестьянка имела в k раз больше яиц, чем первая. Выручили они одинаковые суммы; это значит, что первая крестьянка продавала свои яйца в k раз дороже, чем вторая. Если бы перед торговлей они поменялись яйцами, то первая крестьянка имела бы в k раз больше яиц, чем вторая, и продавала бы их в k раз дороже. Это значит, что она выручила бы в k² больше денег, чем вторая. Следовательно, имеем: k²=15 : 6 2/3=45:20=9:4. Откуда k=3,5Теперь остается 100 яиц разделить в отношении 3:2. Легко находим, что первая крестьянка принесла 40 яиц, вторая 60.
Задача 5. Стая обезьян (индусская задача) : На две партии разбившись, Забавлялись обезьяны. Часть восьмая их в квадрате В роще весело резвилась; Криком радостным двенадцать Воздух свежий оглашали. Вместе сколько, ты мне скажешь. Обезьян там было в роще?
Решение: Общая численность стаи х, тогда (х:8)²+12=х. Откуда х1=48, х2=16. Оба ответа удовлетворяют задаче.
Задача 6. Продажа кур. Три сестры пришли на рынок с курами. Одна принесла для продажи 10 кур, другая 16, третья 26. До полудня они продавали часть своих кур по одной и той же цене. После полудня, опасаясь, что не все куры будут проданы, они понизили цену и распродали оставшихся кур снова по одинаковой цене. Домой все они вернулись с одинаковой выручкой: каждая сестра получила от продажи 35 рублей. По какой цене продавали кур до и после полудня?
Задачи из книги Богдановича М.В. «Математические роднички».
1.Два брата получили в наследство землю, которую должны поделить поровну. Старший брат пожелал, чтобы у него было на 4 десятины больше, чем у младшего. Младший брат согласился, но попросил вернуть ему 200 рублей. Во сколько браться оценили десятину земли?
Решение: Т.е. младший брат должен передать старшему две десятины земли (тогда у старшего будет на 4 десятины земли больше). Значит, две десятины земли стоят 200 рублей, а одна – 200: 2 = 100р.
Ответ: Одна десятина земли стоит 100 рублей.
Решение: Пусть мужик купил х м сукна третьего вида, тогда второго вида он купил (х + 9) м, а первого вида – (х + 9) + 12. А всего он взял 120 м сукна трех видов.
Составим и решим уравнение:
х + (х + 9) + (х + 9) +12 = 120, х + х + 9 + х + 9 + 12 = 120, 3х + 30 = 120, 3х = 90, Х = 30.
Значит мужик взял 30 м сукна третьего вида. Тогда сукна второго вида он взял 30 + 9 = 39 м, а первого – 39 + 12 = 51м.
Ответ: 1 вида – 51м, 2 вида – 39м, 3 вида – 30 м.
3.У пастуха, который вел 60 быков спросили: «Какую часть быков своего многочисленного стада ты ведешь?» Он ответил: «Я веду половину от трети стада». Сколько быков было в стаде?
Решение: Если 60 быков – это половина трети стада, то треть всего стада – это 60*2 = 120 быков. Тогда все стадо – это 120*3 = 360 быков.
Ответ: В стаде было 360 быков.
4. Надо разделить 20 мер пшеницы между 10 людьми так, чтобы каждый мужчина получил 3, каждая женщина 2, а каждый ребенок 1 меру. Сколько мужчин, женщин и детей? (Решить методом перебора).
1 случай: 1 мужчина, 8 женщин и 1 ребенок.
2 случай: 2 мужчин, 6 женщин и 2 ребенка.
3 случай: 3 мужчины, 4 женщин и 3 ребенка.
4 случай: 4 мужчины, 2 женщины и 4 ребенка.
5. Расстояние между городом и селом 588 верст. Путник, который идет из села в город, проходит это расстояние за 21 день, а второй путник, который идет с города в село, проходит это расстояние за 28 дней. Оба путника вышли одновременно. На какой день они встретятся?
Решение: Первый путник проходит за один день 588: 21 = 28(км).
Второй путник проходит за один день 588: 28 = 21(км).
Вдвоем они проходят за день 21 + 28 = 49 (км).
Тогда встретятся она через 588:49 = 12 дней.
Задачи от команды Великолепная восьмерка ID 212
Задача Л.Н. Толстого. Покупатель выбрал в магазине шапку стоимостью в 10 рублей и дал продавцу двадцатипятирублевку. У того не оказалось сдачи, и он послал полученную двадцатипятирублевку для размена в соседнюю лавку. Покупатель получил шапку и 15 рублей сдачи. Когда покупатель ушел, пришел сосед купца, который сказал, что двадцатипятирублевка фальшивая. Первый купец вернул соседу 25 рублей. Спрашивается, сколько хозяин магазина понес в этом деле убытку
Решение. Хозяин из лавки отдал шапку стоимостью 10 руб, сдачу 15 руб и еще 25 рублей купцу соседу. Т.е. потерял 10+15+25=50 руб.
Задача Пауссона. Известному французскому математику Пауссону в детстве попала задача, решив которую, Пауссон увлекся математикой и посвятил ей жизнь. Некто имеет 12 пинт вина и хочет подарить из этого количества половину, но у него нет сосуда в 6 пинт. У него два сосуда: один — в 8 пинт, другой — в 5 пинт. Спрашивается: каким образом налить б пинт в сосуд на 8 пинт?
Решение 1) оставить 3 пинты вина в среднем. 2) перелить эти 3 пинты в пустой малый бидон. 3) из полного бидона отлить 2 пинты в малый
Старинная задача. Крестьянка несла на базар в корзине яйца. Всадник случайно толкнул корзинку, и все яйца разбились. «Сколько у тебя было яиц? — спросил он. «Не знаю, — ответила крестьянка. — Но помню, что когда я раскладывала их по 2, по 3, по 4, по 5, по 6, то каждый раз одно яйцо было лишним, а когда разложила по 7, то остатка не было». Сколько было яиц в корзине, если известно, что там их меньше сотни? Решение Яиц в корзине может быть больше 7 и их число кратно 7. но не делятся на 2, 3, 4, 5, 6. Если взять 49=7*7, то при делении на пять в остатке получим 4, а не 1, как в условии задачи. Следующие кратные7: 7*8, 7*9, и т.д до 7*10 мы взять не можем, т.к получим числа кратные 2, 3, 4, 5, 6. Если взять 77= 7*11, то при делении на 5 получим остаток 2. 7*12 кратно 6. Проверим 7*13=91, это число удовлетворяет всем условиям задачи. Ответ : в корзине было 91 яйцо.
Задача Ньютона о быках. Задача, впрочем, придумана не самим Ньютоном; она является продуктом народного математического творчества. «Три луга, покрытые травой одинаковой густоты и скорости роста, имеют площади: 3 га, 10 га и 24 га. Первый прокормил 12 быков в продолжение 4 недель; второй — 21 быка в течение 9 недель. Сколько быков может прокормить третий луг в течение 18 недель?». РешениеВведем вспомогательное неизвестное у, означающее, какая доля первоначального запаса травы прирастает на 1 га в течение недели. На первом лугу в течение
недели прирастает травы 3 1/3у, а в течение 4 недель 3 1/3у* 4 = 40/3у того запаса, который первоначально имелся на 1 га. Это равносильно тому, как если бы первоначальная площадь луга увеличилась и сделалась равной (3 1/3 + 40/3 у) гектаров. Другими словами, быки съели столько травы, сколько покрывает луг площадью в (3 1/3 + 40/3 у) гектаров. В одну неделю 12 быков поели четвертую часть этого количества, а 1 бык в неделю 1/48 часть, т. е. запас, имеющийся на площади (3 1/3 + 40/3 у):48 = (10+40у)/144 гек¬таров. Подобным же образом находим площадь луга, кормящего одного быка в течение недели из данных для второго луга: недельный прирост на 1 га— у, 9-недельный прирост на 1 га— 9у, 9-недельный прирост на 10 га- 90у. Площадь участка, содержащего запас травы для прокормления 21 быка в течение 9 недель, равна 10+90у. Площадь, достаточная для прокормления 1 быка в течение недели,— (10+90у)/(9*21)=(10+90у)/189 гектаров. Обе нормы прокормления должны быть оди¬наковы: (10+40у)/144=(10+90у)/189 Решив это уравнение, находим у = 1/12 Определим теперь площадь луга, наличный запас травы которого достаточен для прокормления одного быка в течение недели: (10+40У)/144=5/54 гектаров. Наконец, приступаем к вопросу задачи. Обозначив искомое число быков через х, имеем: (24+24*18*1/12)/(18*х)=5/54 откуда х =36. Третий луг может прокормить в тече¬ние 18 недель 36 быков.
Дэдвудский экспресс Дэдвудский экспресс доставил в шахтерский городок два ящика для одной молодой леди. Между проводником и шахтерами, приятелями этой леди, которые явились за грузом, произошел спор. Дело в том, что проводник хотел взять уплату за провоз ящиков согласно прейскуранту – по 5 долларов за кубический фут. А шахтеры упрямо отказывались платить на подобных условиях, утверждая, что по действующим на шахтах законам всегда платят за погонный фут. Да и вообще молодые люди не могли понять, какое право имеет железнодорожная компания касаться «кубического содержимого» ящиков юной леди! Проводнику в конце концов пришлось принять их условия: он измерил длину ящиков и взял по 5 долларов за погонный фут. Оба ящика имели форму правильных кубов, и один был ровно вдвое ниже другого. Само странное состоит в том, что, приложив ящики друг к другу и измерив их суммарную длину, проводник обнаружил, что в обоих случаях цены за провоз не отличаются даже на одну тысячную цента: можно было с равным успехом брать по 5 долларов как за кубический, так и за погонный фут. Каковы размеры двух ящиков?
Сватовство сиамского короля
Принцесса хочет испытать своего, королевских кровей поклонника, показываю ему план ее любимого сада. В саду растут 8 яблонь и 8 грушевых деревьев, каждое дерево изображено на плане в виде соответствующего плода. Начав с любой из восьми груш, следует отметить наикратчайший путь, который проходил бы через все 16 плодов и кончался в «сердечке», на которое указывает принцесса. Числа на плодах расставлены просто для удобства «соискателей». Не сумеете ли вы обнаружить более короткий путь, чем тот, который предложил сиамский король?
Решение:Если все 4 источника заполнят бассейн за x дней то, 12x/12+6x/12+4x/12+3x/12=12/12,12x+6x+4x+3x=12,25x=12,x=12/25. Потребуется 12/25 дня.
Задача №31. Задача Ньютона
Два почтальона А и В находятся в 59 км друг от друга. Утром они отправляются навстречу друг другу. Почтальон А за два часа проходит 7 км, почтальон В проходит 8 км за 3 часа, причем он выходит на 1 час позднее, чем А. Сколько километров пройдет А до встречи с В?
скорость В: 8/3 км/ч, скорость сближения 7/2+8/3=(21+16)/6=37/6(км/ч)
за 1 час А проходит 3.5 км, до выхода В он пройдет 3,5км, значит,останется пройти 59-3,5=55,5 км. Время В до встречи: 55,5/37/6=9(ч)
Следовательно, А до встречи с В будет идти 10 часов.
Задача №32 Монах вышел в 8 часов утра из монастыря и за 12 часов поднялся на гору. На следующее утро в 9 часов он отправился той же дорогой в обратный путь и к 8 часам вечера попал в монастырь. Найдется ли на пути точка, в которой его часы показывали одинаковое время в первый и во второй день путешествия?
Представим, что у нас 2 путешественника выходят одновременно из разных пунктов. Они движутся на встречу друг другу. Они обязательно встретятся в какой-то момент времени в какой-то точке. Значит, такая точка найдется.
Задачи аналогичные №33, встречаются в разных вариантах у отдельных народов.
Египетский писец Ахмес, писавший свой конспект между 1780 и 1580 гг. до н.э. предлагает задачу:
По-видимому, смысл задачи следующий:
«В семи домах имеется по семь кошек (7*7=49), каждая кошка съедает по семь мышей (7*49=343), каждая мышь уничтожает по семь колосьев (7*343=2401), каждый колос дает по семь мер зерна (7*2401=16807), вместе составляет19607»
Задача интересна уже тем, что показывает знание египтянами степеней числа.
В книге Леонардо Пизанского (1202г) задача имеет форму:
Решение как в задаче №33
В 1801г в Соединенных Штатах Америки в «Школьной арифметике» Д.Адамса дана задача св стихотворной форме.
Русский перевод задачи (Е.И. Игнатьев):
В Сент-Айвз как-то я шагал
И семь женщин повстречал,
И у каждой семь мешков,
А в мешках по семь котов,
У котов по семь котят.
Сколько всех пройти хотят
В Сент-Айвз: женщин и мешков,
Решение как в задаче №33
Русская редакция задачи, записанная профессором И.Ю.Тимченко в Орловской губернии:
У каждого старца по семи костылей,
На каждом костыле по семи сучков,
На каждом сучке по семи кошелей,
В каждом кошеле по семи пирогов,
В каждом пироге по семи воробьев,
Решение как в задаче №33
—Гимназисты 11:30, 28 октября 2008 (UZT) Старинная задача Л.Ф. Магницкого
Условие: Един человек выпьет кадь пития в 14 дней, а со женою выпьет тоеже кадь в 10 дней, и ведательно есть, в колико дней жена его способно выпьет тоеже кадь?
Найдем, какую часть питья жена выпивает за один день:
1/10 – 1/14 = 2/70 = 1/35 кади
Следовательно, всю кадь питья жена выпивает за 35 дней.
Ответ: Жена способна выпить кадь питья за 35 дней.
—Гимназисты 11:30, 28 октября 2008 (UZT)
Старинная задача среднеазиатского ученого Бируни
Условие: Если 10 дирхемов приносят доход 5 дирхемов в два месяца, какой доход принесут 8 дирхемов за три месяца?
Найдем, сколько дирхемов дохода приносят 10 дирхемов за один месяц:
Тогда один дирхем за один месяц приносит доход:
Найдем, какой доход приносят 8 дирхемов за один месяц:
Тогда за три месяца 8 дирхемов приносят доход:
Задача Эйнштейна А. Эйнштейн придумал эту задачу в прошлом веке и полагал, что 98% жителей Земли не в состоянии ее решить. Принадлежите ли вы к 2% самых умных людей планеты? Здесь нет никакого фокуса, только чистая логика.
1. Есть 5 домов каждый разного цвета. 2. В каждом доме живет по одному человеку отличной друг от друга национальности. 3. Каждый жилец пьет только один определенный напиток, курит определенную марку сигарет и держит определенное животное. 4. Никто из 5 человек не пьет одинаковые с другими напитки, не курит одинаковые сигареты и не держит одинаковое животное.
Вопрос: кому принадлежит рыба?
Это всё, что необходимо для решения задачи.
Задача № 1—Искатели ID 249 18:54, 28 октября 2008 (UZT)
Три брата получили 24 яблока. Каждый получил столько, сколько ему лет. Младший предложил: «Я оставлю себе половину, а остальные разделю между вами. Пусть потом средний оставит себе половину. А остальные разделит между нами поровну. Потом старший оставит себе половину, а остальные разделит между мною и средним поровну.» Братья согласились. В результате у всех яблок оказалось поровну. Сколько лет каждому брату?
В конце обмена у каждого стало по 24:3=8 яблок. Старший оставил себе половину, а остальные разделил между братьями. Следовательно, у старшего было 8*2=16 яблок, у среднего 8-8:2=4 яблока и у младшего 8-8:2=4 яблока. Средний оставил себе половину, а остальные разделил между братьями. Следовательно, у среднего его было 4*2=8 яблок, у старшего 16-4:2=14 яблок и у младшего 4-4:2=2 яблока. Младший оставил себе половину, а остальные разделил между братьями. Следовательно, у младшего было 2*2=4 яблока, у среднего 8-2:2=7 яблок и у старшего 14-2:2=13 яблока.
Ответ: Старшему брату 13 лет, среднему 7 лет и младшему 4 года.
Задача № 2—Искатели ID 249 18:54, 28 октября 2008 (UZT)
в кашолке плюшки нёс.
И на лесной опушке
Он половину плюшек съел
И плюс ещё полплюшки.
Шёл, шёл. Уселся отдохнуть.
И под «ку-ку» кукушки
Вновь половину плюшек съел
И плюс ещё полплюшки.
Стемнело. Он ускорил шаг.
И на крыльце избушки
Он снова пол остатка съел
И плюс ещё полплюшки.
Он в дом вошёл уныло…
Хочу чтоб мне сказали вы, А сколько плюшек было?
Задача № 3—Искатели ID 249 18:58, 28 октября 2008 (UZT)
Осталось 8 картофелин. Следовательно, 3-й съел 8:2=4 картофелины. Когда он проснулся, было 8+4=12 картофелин. 2-й оставил 12, следовательно, съел 12:2=6. Когда он проснулся, было 12+6=18 картофелин. 1-й оставил 18, следовательно, съел 18:2=9. Когда он проснулся, было 18+9=27 картофелин.
Ответ: хозяйка сварила 27 картофелин.
Задача № 4—Искатели ID 249 18:58, 28 октября 2008 (UZT)
Андрей и Фёдор обменивались деньгами. Сначала Андрей отдал Фёдору часть денег, потом Фёдор Андрею, затем опять Андрей Фёдору, и, наконец, Фёдор Андрею в последний раз. После чего у каждого стало по 160 рублей. Количество переданных денег всякий раз было равно количеству денег у получавшего. Сколько денег было у Андрея и Фёдора первоначально?
Осталось по 160 рублей. Следовательно, во время 4-го обмена Фёдор отдал Андрею 160:2=80 рубле. До этого у Фёдора было 160+80=240 рублей, а у Андрея 160-80=80 рублей. Во время 3-го обмена Андрей отдал Фёдору 240:2=120 рубле. До этого у Фёдора было 120 рублей, а у Андрея 80+120=200 рублей. Во время 2-го обмена Фёдор отдал Андрею 20:2=100 рубле. До этого у Фёдора было 120+100=220 рублей, а у Андрея 200-100=100 рублей. Во время 1-го обмена Андрей отдал Фёдору 220:2=110 рубле. До этого у Фёдора было 110 рублей, а у Андрея 100+110=210 рублей.
Ответ: у Федора было 110 руб., у Андрея было 210 руб.
Задача № 5—Искатели ID 249 17:26, 13 ноября 2008 (UZT)
Человек покупал масло. Когда он давал деньги за 8 бочек масла, у него осталось 20 алтын. Когда он хотел купить 9 бочек, ему не хватало 1,5 рубля с гривною. Сколько денег было у этого человека? 
Задача № 6—Искатели ID 249 18:14, 13 ноября 2008 (UZT)
Хозяин нанял работника на 1 год и пообещал дать ему 12 рублей и кафтан. Но работник отработал только 7 месяцев. При расчёте хозяин дал ему 5 рублей и кафтан. Сколько стоит кафтан? 
Задача № 7—Искатели ID 249 18:14, 13 ноября 2008 (UZT)
Хозяин нанял работника с условием: за каждый рабочий день будет платить по 20 копеек, а за каждый нерабочий – вычитать 30 копеек. По прошествии 60 дней работник ничего не заработал. Сколько было рабочих дней? 
Задача № 8—Искатели ID 249 18:14, 13 ноября 2008 (UZT)
Один человек купил 112 баранов старых и молодых, заплатив за них 49 рублей и 20 алтын. За старого барана он платил по 15 алтын и 4 полушки, а за молодого по 10 алтын. Сколько каких баранов было куплено? 
Участник:Истина_ID_218
Старинные китайские задачи
19х+1 = 17y+14+12z
19x = 12z
x = 12z/19
Поскольку x, y, z суть целые положительные числа, можно принять, что
Возьмем наименьшее значение t при ктором у будет целым положительным(14)
x = 168
y = 187
z = 266
Задача о глубине озера.
В середине квадратного озера со стороной 10 футов растет тростник, выходящий из воды на 1 фут. Если нагнуть тростник, вершина достигнет берега. Как глубоко озеро? Ответ. 12 футов.
Задача о прямоугольном треугольнике.
Определить стороны прямоугольного треугольника, если известны площадь и периметр.
Решение. Составим систему из трех уравнений с тремя неизвестными:
a+b+c = p;
a^2+b^2 = c^2;
ab/2 = s;
Из 2-го и 3-го уравнений имеем:
(a+b)^2 = 4s+c^2
(p-c)^2 = 4s+c^2
Решая относительно с получим:
c = (p^2-4s)/2p
a+b = (p^2-4s)/2p
Присоединяя к этому уравнению 3-е, значения a и b определяем как корни квадратного уравнения:
x^2-(p^2-4s)/2p*x+2s = 0.
—Bookworm ID 213 14:54, 28 октября 2008 (UZT) Задача № 22. Задача Л. Н. Толстого: Пять братьев разделили после отца наследство поровну. В наследстве было три дома. Так как три дома разделить было нельзя на 5 частей, то их взяли три старших брата, а меньшим за то выделили деньги. Каждый из трех братьев заплатил по 800 р. Меньшие братья разделили эти деньги между собой, и тогда у всех стало поровну. Много ли стоит один дом? Решение: Сначала узнаем, сколько денег получили младшие братья: 800*3:2=1200 рублей. След-но у всех братьев наследство оценивается в 1200*5=6.000 рублей. Значит стоимость дома 6000:3=2000 рублей. Ответ: 2000 рублей.
Участник:Максимум ID-251
Летела стая уток. Одна впереди, две позади; одна позади и две впереди; одна между двумя и три в ряд. Сколько летело уток? Ответ: Летели одна за другой три утки
Задачка для второго класса церковноприходской школы. Придумана Львом Толстым. Сейчас ее правильно могут решить только 30% старшеклассников и только 20% студентов ВУЗов ЗАДАЧА Продавец продает шапку. Стоит 10 р. Подходит покупатель, меряет и согласен взять, но у него есть только 25 р. Продавец отсылает мальчика с этими 25 р. к соседке разменять. Мальчик прибегает и отдает 10+10+5. Продавец отдает шапку и сдачу в 15 руб. Через какое то время приходит соседкаи и говорит, что 25 р. фальшивые, требует отдать ей деньги. Ну что делать. Продавец лезет в кассу и возвращает ей деньги. ВОПРОС: на сколько обманули продавца? Ответ: Рассуждаем: доходы продавца: 25р от мальчика расходы: шапка (10р) + сдача (15р) + соседка(25р) итого 50-25=-25, т.е. убыток 25р Можно рассуждать и по другому: соседка осталась при своих деньгах (25р отдала на размен, потом 25р забрала у торговца), т.е. ее можно не учитывать. Покупатель ушел с 15р сдачи и шапкой за 10р, т.е. убыток торговца составил как раз 25р (15р сдачи + 10р шапка)
Как разделить 5 яблок между пятью лицами так, чтобы каждый получил по яблоку и одно яблоко осталось в корзине. Ответ: Один человек берет яблоко вместе с корзиной.
В банку попал 1 микроб, и через 35 минут банка была наполнена микробами, причем известно, что количество микробов ежеминутно удваивалось. За сколько минут банка была наполнена микробами на половину? Ответ: За 34 минуты, т. к. за 35 минут банка будет уже заполнена.
У Козьмы Пpуткова есть такая коpоткая басня, котоpая называется «Пастух, молоко и читатель»: Однажды нес пастух куда-то молоко, Да так ужасно далеко, Что уж назад не возвpащался. Читатель! Он тебе не попадался? И, пpи пpочтении этого четвеpостишия вспоминается такая очень дpевняя задача, на котоpую большинство дает ответ очень быстpо и очень непpавильно: ЗАДАЧА: Если идти все вpемя на севеpо-восток, то куда пpидешь? Hо вы-то пpежде чем писать ответ, подумаете, пpавда? А pешив эту несложную задачку, подумайте над втоpым вопpосом: Будет ли путь бесконечным? Ответ: Если идти все вpемя на севеpо-восток, то пpидешь на севеpный полюс. Путь бесконечным не будет, и это легко доказывается. Действительно, если мы пойдем со скоpостью v, то будем в нашем случае постоянно пpиближаться к полюсу со скоpостью v/sqrt(2), независимо от шиpоты местности. Так как pасстояние от любой точки земной повеpхности до полюса конечно, конечен и наш путь.
На столе лежат две одинаковые монеты. Пусть одна из них лежит неподвижно, а другая обкатывается вокруг нее, все время с нею соприкасаясь. Сколько оборотов вокруг своей оси сделает вторая монета, обойдя один раз вокруг неподвижной монеты? Ответ: Вторая монета дважды повернется вокруг своей оси.
Задачи из книги Р. Смаллиана «Как же называется эта книга?»
В темной комнате стоит шкаф, в ящике которого лежат 24 красных и 24 синих носка. Сколько носков следует взять из ящика, чтобы из них заведомо можно было составить по крайней мере одну пару носков одного цвета? (В этой и в следующей задаче речь идет о наименьшем числе носков.) Ответ: Обычно на вопрос задачи дают неправильный ответ: 25 носков. Если бы в задаче спрашивалось, сколько носков следует взять из ящика, чтобы среди них было по крайней мере 2 носка различного цвета, то правильный ответ действительно был бы таким: 25 носков. Но в нашей задаче речь идет о том, чтобы среди взятых из ящика носков по крайней мере 2 носка были одного цвета, поэтому правильный ответ задачи иной: 3 носка. Если я возьму из ящика 3 носка, то они либо все будут одного цвета (и в этом случае я заведомо смогу выбрать из них по крайней мере 2 носка одного цвета), либо 2 носка будут одного цвета, а третий носок другого, что позволит мне также составить пару одноцветных носков.
Поезд отправляется из Бостона в Нью-Йорк. Через час другой поезд отправляется из Нью-Йорка в Бостон. Оба поезда едут с одной и той же скоростью. Какой из них в момент встречи будет находиться на меньшем расстоянии от Бостона? Примечание: размерами (длиной) поездов можно пренебречь. Ответ: Поезда в момент встречи будут находиться на одинаковом расстоянии от Бостона.
—Максимум ID 251 16:44, 28 октября 2008 (UZT)
Задача №37. Из «Курса чистой математики» Е.Д. Войтяховского.
Служилому воину дано вознагрождение за первую рану 1 к., за вторую 2 к., за третью 4 к., и т.д. Всего воик получил 655 р. 35 к. Спрашивается число его ран.
1,2,4,8,10. Знаменатель равен 2.
Сумма 65535. S(n) = 1*(1-q^n)/(1-q)
(1-2^n)= 65535*(1-2), 65536=2^n, n =16
Задача №38. Древний Вавилон. Второе тысячелетие до нашей эры.
«10 братьев, 5/3 мины серебра. Брат над братом поднимается, на сколько поднимется не знаю. Доля восьмого 6 шекелей. Брат над братом на сколько выше?»
Здесь требуется по сумме первых 10 членов арифметической прогрессии 5/3 мины ( 1 мина = 60 шекелей) и известному 8-му члену определить разность арифметической прогрессии.
A + 7d = 6, 5*60/3 = (2A +9d)*10/2,
100/5 = 2A+9d, A= 6-7d. 2(6-7d)+9d=20, 5d=-8, d=-1,6.
Идёт крестьянин и плачет: «Эхма! Жизнь моя горькая! Заела нужда совсем! Вот в кармане только несколько грошей медных болтается, да и те сейчас нужно отдать. И как это у других бывает,что на всякие свои деньги они ещё деньги получают? Право, хоть бы кто помочь мне захотел».
Только успел это сказать, как глядь, а перед ним чёрт стоит.
Перешёл он через мост один раз, посчитал деньги. Действительно, стало вдвое больше. Бросил он 24 копейки чёрту и перешёл через мост второй раз. Опять денег стало вдвое больше, чем перед этим.Отсчитал он 24 копейки, отдал чёрту и перешёл через мост в третий раз. Денег стало снова вдвое больше. Но только и оказалось их ровнёхонько 24 копейки, которые по уговору. он должен был отдать чёрту. Отдал он их и остался без копейки.
Сколько же у крестьянина было денег сначала?
Задача разрешается очень легко, если решение её начать с конца, приняв во внимание, что после третьего перехода у крестьянина оказалось ровно 24 коп., которые он должен был отдоть.
Если после последнего перехода у крестьянина оказалось 24 коп., то, значит, перед этим переходом у него было 12 коп. Но зти 12 коп., получилось после того, как он отдап 24 коп., значит, всего у него было 36 коп. Следовательно, второй переход он начал с 18 коп., а эти 18 коп. получились у него после того, как он в первый разперешёл мост и отдал 24 коп. Значит всего после первого перехода у него было денег 18+24=42 коп. Отсюда ясно, что перед тем, как первый раз вступить на мост, крестьянин имел в кармане 21 коп. собственных денег.
1. (Задача, приписываемая Эйлеру). Решив все свои сбережения поделить поровну между всеми своими сыновьями, некто составил такое завещание. «Старший из моих сыновей должен получить 1000 руб. и 1/8 часть остатка; следующий – 2000 руб. и 1/8 нового остатка; третий сын – 3000 руб. и 1/8 часть третьего остатка и т.д.». Определить число сыновей и размер завещанного сбережения.
Решение: Так как все сыновья получили поровну, то 1/8 часть каждого нового остатка была на 1000 руб. меньше 1/8 части предыдущего остатка, а, значит, весь новый остаток был на 8000 руб. меньше предыдущего. Так как, по условию, все деньги были поделены полностью, то, когда младший сын получил по завещанию, кроме нескольких тысяч рублей, ещё 1/8 часть остатка, этого остатка не оказалось. Но тогда предыдущий остаток 8000 руб. Из него предпоследний сын получил 1/8 часть, равную 1000 руб., а остальные 7000 руб. получил младший сын, который, таким образом, был седьмым сыном. ОТВЕТ: сыновей было 7, а завещанная сумма 7000*7=49000 (руб.)
2. Задача №64 из папируса Райнда. «Пусть тебе сказано: раздели 10 мер ячменя между десятью людьми; разница между каждым человеком и его соседом должна составлять 1/8 меры зерна».
1) 1/8+2/8+3/8+4/8+5/8+6/8+7/8+8/8+9/8=45/8 (мер) – на столько меньше мер, если было бы поровну.
2) 10-45/8=35/8 (мер) – ячмень на 10 человек
3) 35/8/10=35/80=7/16 (мер) – получит 1 человек, остальные – каждый на 1/8 мер больше.
—Борей ID 238 12:40, 29 октября 2008 (UZT)
Внимание! Если вы увидите сообщение что количество опубликованных знаков превышает длину страницы, то вы можете разместить свои задачи на странице Копилка знаменитых задач продолжение 5