Что влияет на период маятника
Математический маятник
Содержание:
Определение
Представьте себе некую механическую систему, которая состоит из некой материальной точки (тела), которая висит на нерастяжимой невесомой нити (при этом масса нити ничтожно мала по сравнению с массой тела). Вот такая механическая система и является маятником или осциллятором, как его еще называют. Впрочем, могут быть и другие виды такого устройства. Чем же математический маятник, осциллятор интересен для нас? Дело в том, что с его помощью можно проникнуть в суть многих интересных природных явлений в физике.
Колебания
Формула периода колебания математического маятника впервые была открыта голландским ученым Гюйгенсом в далеком XVII веке. Будучи современником Исаака Ньютона, Гюйгенс был очень увлечен такими вот маятниками, увлечен настолько, что даже изобрел специальные часы с маятниковым механизмам, и часы эти были одними из самых точных для того времени.
Маятниковые часы Гюйгенса.
Появление подобного изобретения сослужило большую пользу физике, особенно в сфере физических экспериментов, где точное измерение времени является весьма важным фактором.
Но вернемся к маятнику, итак, в основе работы маятника лежат его колебания, которые можно выразить формулой, точнее следующим дифференциальным уравнением:
Где х (t) – неизвестная функция (это угол отклонения от нижнего положения равновесия в момент t, выраженный в радианах); w – положительная константа, которая определяется из параметров маятника (w = √ g/L, где g – это ускорение свободного падения, а L – длина математического маятника (подвес).
Помимо, собственно колебаний маятник может пребывать и в положении равновесия, при этом сила тяжести, действующая на него, будет уравновешиваться силой натяжения нити. Обычный плоский маятник, пребывающий на нерастяжимой нити, является системой с двумя степенями свободы. Но если, к примеру, нитку заменить на стержень, тогда наш маятник станет системой лишь с одной степенью свободы, так как его движения будут двухмерными, а не трехмерными.
Но если же наш маятник все-таки пребывает на нити и при этом совершает интенсивные колебания вверх-вниз, тогда механическая система приобретает устойчивое положение, именуемое «верх тормашками», еще ее называют маятником Капицы.
Свойства
У маятника есть ряд интересных свойств, подтвержденных физическими законами. Так период колебаний всякого маятника зависит от таких факторов, как его размер, форма тела, расстояние между центром тяжести и точкой подвеса. Поэтому определение периода маятника является не простой задачей. А вот период математического маятника можно рассчитать точно по формуле, которая будет приведена ниже.
В ходе наблюдений за маятниками были выведены следующие закономерности:
Период
Период маятника – показатель, который представляет период собственно колебаний маятника, их длительность. Формулу периода математического маятника можно записать следующим образом.
Где L – длина нити математического маятника, g – ускорение свободного падения, а π – число Пи, математическая константа.
Период малых колебания математического маятника никак не зависит от массы маятника и амплитуды колебания, в этой ситуации он двигается как математический маятник с заданной длинной.
Практическое применение
Вот мы добрались и до самого интересного, зачем нужен математический маятник и какое его применение на практике в жизни. В первую очередь ускорение математического маятника используется для геологоразведки, с его помощью ищут полезные ископаемые. Как это происходит? Дело в том, что ускорение свободного падения изменяется с географической широтой, так как плотность коры в разных местах нашей планеты далеко не одинакова и там где залегают породы с большей плотностью, ускорение будет немножко больше. А значит, просто подсчитав количество колебаний маятника можно отыскать в недрах Земли руду или каменный уголь, так как они имеют большую плотность, нежели другие рыхлые горные породы.
Также математическим маятником пользовались многие выдающиеся ученые прошлого, начиная с античности, в частности Архимед, Аристотель, Платон, Плутарх. Так Архимед и вовсе использовал математический маятник во всех своих вычислениях, а некоторые люди даже верили, что маятник может влиять на судьбы людей и пытались делать с его помощью предсказания будущего.
Видео
И в завершение образовательное видео по теме нашей статьи.
Система параметров маятника
Одним из механических объектов, демонстрирующих периодическое движение, является маятник.
Маятник-это устройство, которое движется вперед и назад, когда на него воздействует внешняя сила. Параметры маятника зависят от его длины, момента инерции и других условий. Устройства по этому принципу широко используются в часах, сейсмометрах и метрономах.
Когда на маятник воздействует внешняя сила из своего равновесного положения, он поднимается, а затем опускается под действием гравитационной силы. Угловая скорость увеличивается, когда частица находится в своей самой низкой точке, и уменьшается, когда частица достигает своей высшей точки.
История открытия
Маятники использовались в качестве сейсмометра для измерения землетрясений в первом веке династии Хань. После этого они были использованы для измерения времени египетским астрономом Ибн Юнусом в десятом веке.
Итальянский физик и астроном Галилео Галилей открыл принцип колебательного движения маятника и попытался изучить параметры и свойства этого простейшего устройства.
Заинтригованный, Галилей решил измерить, сколько времени уходит на каждый взмах, используя единственное приблизительно периодическое событие, к которому он был готов: биение собственного пульса. Он обнаружил кое-что интересное: число ударов сердца между качаниями люстры было примерно одинаковым, независимо от того, были ли качели широкими или узкими. Величина колебаний — как далеко качался маятник взад и вперед-не влияла на частоту этих колебаний.
В своих экспериментах Галилей установил, что параметр время, необходимое для возвратно-поступательного движения маятника заданной длины, остается неизменным, даже если его дуга, или амплитуда, уменьшается. Определив параметры маятника Галилей открыл изохронизмы, наиболее важные характеристики, которые делают их полезными для измерения времени.
Галилей открыл такие свойства и параметры маятника, как: временная и периодическая независимость маятника от его амплитуды и массы.
Он сказал, что период маятника прямо пропорционален квадратному корню из длины маятника. Кроме того в истории телескопа он также поучаствовал. Первые маятниковые часы были сконструированы сыном Галилея в 1641 году.
Маятник, происходящий от латинского слова «pendulus», означающего «висящий», — это тело, которое висит на неподвижной точке, которая, когда ее тянут назад и отпускают, качается взад и вперед.
Существует множество применений маятника в повседневной жизни. Некоторые примеры могут быть маятниковыми часами, которые использовались в качестве хранителя времени, метрономом, который используется для поддержания скорости музыки, акселерометрами, которые измеряют значения ускорения, и сейсмометрами, которые используются для измерения землетрясений.
Возможно, самым известным маятником является Маятник Фуко, который показал вращение Земли в середине 1800-х гг.
Почти в каждом крупном научном музее есть маятник, который можно увидеть в движении.
Система параметров устройства маятника
Инерция
Инерция маятника — сопротивление физического объекта — это то, что заставляет его качаться прямо и вверх. Нисходящая сила тяжести, которая заставляет два объекта притягиваться друг к другу, — это то, что тянет маятник прямо назад. Другая сила, сопротивление воздуха, определяющая скорость движения маятника, заставляет его раскачиваться по более коротким дугам.
Период
Период — это количество времени, которое требуется, чтобы сделать одно качание. Период маятника длиной 1 метр составляет 2 секунды.
Период связан с длиной устройства, но эта зависимость не линейна. Параметр маятника в виде периода, который в два раза длиннее другого, не просто имеет период, который также в два раза длиннее.
Амплитуда
Амплитуда-это максимальное смещение из равновесного положения. Когда маятник находится в покое, а не качается, он висит прямо вниз. Это положение называется «положением равновесия». Это положение удобно рассматривать как исходное, упомянутое в определении как «начало координат». При таком происхождении положение изменяется влево и вправо от начала координат. Величина наибольшего расстояния от начала координат называется амплитудой. Предмет качается на расстояние, равное амплитуде слева, а затем качается на расстояние, равное амплитуде справа.
Скорость
Скорость говорит о скорости изменения положения. Во всех случаях есть две вещи, чтобы указать скорость: скорость и направление скорости. Скорость измеряется в метрах в секунду или м/с. Направление описывается стрелкой, указывающей направление движения, или углом между этой стрелкой и исходным направлением, используемым для определения положения.
Ускорение
Ускорение — это скорость изменения скорости. Единицами измерения являются метры в секунду в квадрате или м/сек2. Указывается как величину ускорения, так и его направление. Если направление ускорения совпадает с направлением скорости, то объект ускоряется. Если направление ускорения противоположно скорости, то объект замедляется. Если направление ускорения перпендикулярно направлению скорости, то величина скорости не изменяется, но направление скорости изменяется.
Ускорение отличается от скорости удивительным образом, лучше всего описанным в трех шагах, если
Единственный способ, которым объект ускорится (изменит скорость), — это если он вынужден это сделать. Разумно сказать, что сила имеет направление, и это направление совпадает с направлением ускорения. Большая сила вызывает большее ускорение.
Равнодействующая сила
Равнодействующая сила — это сила, возникающая в результате сочетания двух или более сил. Две силы, действующие на маятник, — это сила тяготения, тянущая прямо вниз, и сила вращения, тянущая вдоль струны к оси. Эти две силы объединяются, чтобы произвести результирующую силу. Точно так же, как стрела толкается вперед двумя половинами тетивы, объект толкается равнодействующей силой, стрела которой «расщепляет» две составляющие силы стрелы.
Гравитация
Гравитация — это название явления, которое одновременно знакомо и загадочно. Нас так уверенно тянет к Земле, что мы принимаем это как должное. Мы используем это явление, чтобы сидеть, ходить, бегать и играть в догонялки.
Экспериментально установлено, что объект, которому позволено свободно падать под действием силы тяжести, ускоряется. Поскольку объект должен быть вынужден ускоряться, должна существовать сила, связанная с гравитацией; мы называем ее силой тяготения. Направление силы тяжести — вниз. На самом деле направление силы тяжести определяет то, что мы подразумеваем под словом «вниз».
Плоскость колебаний
Две силы: гравитация и струна определяют плоскость. Плоскость также определяется струной маятника и направлением вниз. Равнодействующая сила направлена вдоль линии, лежащей в этой плоскости. Ускорение также направлено вдоль линии, лежащей в этой плоскости.
Если объект оттянут назад и освобожден от покоя, скорость направлена вдоль той же линии, что и ускорение, и объект движется вдоль той же линии. Путь лежит вдоль плоскости, определяемой струной и гравитацией. Этот путь лежит в плоскости колебаний.
Поскольку струна и гравитация лежат в плоскости, предполагается, что плоскость колебаний никогда не изменится.
Вращение
Если положение объекта изменяется вдоль круговой траектории, говорят, что объект вращается вдоль этой окружности. Секундная стрелка аналоговых часов вращается по часовой стрелке. Особенность маятника Фуко состоит в том, что плоскость колебаний немного меняет направление по часовой стрелке в северном полушарии из-за суточного вращения Земли.
Работа
Работа — это расстояние, на которое перемещается объект, умноженное на силу, которая толкнула его на это расстояние.
Работа может быть положительной или отрицательной. Если объект движется в том же направлении, что и сила (например, когда грузовик разгоняется), то работа положительна. Если объект движется в направлении, противоположном силе (например, когда грузовик тормозит и замедляется), работа отрицательна.
Когда сила тяжести тянет вниз на предмет, который был сброшен, сила тяжести делает положительную работу на объекте.
Кинетическая энергия
Когда объект оттягивается назад и освобождается от покоя, сила тяжести положительно воздействует на него, когда он качается вниз. После того, как объект проходит через низшую точку, он качается обратно вверх, и во время этого подъема сила тяжести делает отрицательную работу, заставляя его остановиться на вершине качания.
На самом деле, объект качается назад на ту же высоту, что и высота выпуска, поэтому отрицательная работа гравитации на подъеме имеет тот же размер, что и положительная работа гравитации на спуске.
Это похоже на превращение энергии и на то, как если бы работа хранилась некоторое время, а затем возвращена обратно. При преобразовании в скорость работа, как говорят, преобразуется в кинетическую энергию. Говорят, что работа преобразуется в кинетическую энергию, когда работа делается для увеличения скорости.
Потенциальная энергия
Когда маятник оттянут назад, он готов качнуться вниз, приобретая кинетическую энергию. Количество кинетической энергии, которое он способен приобрести, определяется тем, насколько высоко был поднят объект, когда его потянули назад.
Поскольку объект обладает потенциалом для получения этой кинетической энергии, говорят, что он обладает «потенциальной энергией». Получается, что потенциальная энергия пропорциональна высоте над самой нижней точкой качания.
Таким образом, параметры маятника — период, инерция, скорость, ускорение, гравитация, вращение, работа, потенциальная и кинетическая энергии задают свойство этого простейшего механического устройства.
Маятник. Законы колебаний
Одна из легенд гласит, что Галилео Галилей открыл регулярное движение маятника, наблюдая за колебаниями большого светильника в Пизанском соборе. Регулярность этого движения полностью перевернула подход к отсчету времени и в дальнейшем вдохновила ученого на открытие принципов движения.
Даже если эта романтическая история и не совсем правдива, не остается сомнений в том, что Галилео занимался вопросами движения маятника в самом начале своей научной деятельности.
Примерно к 1602 году он обнаружил, что период колебаний обычного маятника пропорционален квадратному корню длины подвеса. Под периодом понимается время, за которое маятник совершает одно колебание, т.е. движение в обоих направлениях. Проще всего представить себе это как время, необходимое для движения из крайне левого положения в крайне правое и обратно, минуя центральную точку. Изменение массы груза маятника никак не повлияло на период его колебаний — с более тяжелым грузом маятник колебался с той же частотой, что и прежде.
Важно то, что Галилей открыл закон малых колебаний, период которых также не зависел и от амплитуды — максимального отклонения маятника от положения равновесия. Это означало, что все маятники одинаковой длины в любой точке Земли будут колебаться с одинаковым периодом. Такое свойство называется «изохронизмом» (что дословно означает «одинаковое время») и делает возможным использование маятника для счета времени. Все, что необходимо для этого, это маятник с периодом колебания 1 секунда. Так Галилей вновь совершил переворот в науке.
Тик-так Счет времени был очень важен для духовенства Средних веков, поскольку их встречи с прихожанами ограничивались лишь определенным временем суток. Механические часы, появившиеся в XIV веке (в Милане — в 1335 году), служили именно этой цели и приводились в движение опускающимся с определенной скоростью грузом.
Точность этих часов была весьма далека от современной, так что их приходилось периодически устанавливать по астрономическим наблюдениям. По причине смерти в 1642 году Галилей не успел построить свои часы с маятником, однако в 1656 году голландский ученый Христиан Гюйгенс сумел создать проект часов, который оказалось возможным реализовать в мастерских. Как и в прежних конструкциях, часы Гюйгенса приводились в движение за счет опускания груза. Однако в них впервые стал использоваться маятник для регуляции хода.
Гюйгенс также провел работу по замене механизма церковных механических часов, что сделало их более точными — за счет перемещения груза вверх и вниз по маятнику с целью подобрать период колебаний ровно в одну секунду. Эти первые механические часы при точной настройке теряли лишь считаные секунды за день.
Маятник является примером гармонических колебаний. Сами колебания происходят под действием так называемой «возвращающей» силы. Она называется так, поскольку всегда направлена в сторону центральной точки, а величина этой силы пропорциональна удалению от центральной точки. Теперь слово молодому английскому физику, применившему те же идеи к описанию того, как растягиваются и сжимаются предметы.
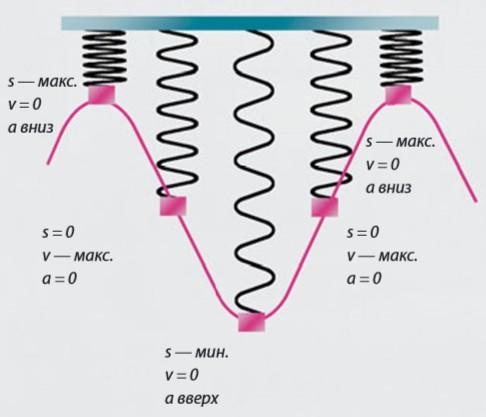
Простые гармонические колебания
Движение маятника является гармоническим колебанием. На рисунке нагруженная пружина совершает свободные колебания по тому же закону, и в идеальном случае, когда при колебаниях не расходуется энергия, это движение может стать моделью простых гармонических колебаний. Соответственно, v — это скорость груза, a — ускорение, s — смещение относительно центральной точки, и все эти параметры в идеальном случае подчиняются строгому механическому закону. В реальности всегда присутствует трение, которое замедляет колебания и через какое-то время их останавливает.
Светильник Галилея
Этот большой светильник все еще висит в Пизанском соборе, где Галилео пришла в голову идея изучать движение маятника. История донесла до нас рассказ о том, что Галилей во время церковных служб использовал ритм колебаний этого светильника, чтобы отсчитывать время. Однако туристам не советуем верить. Этот светильник датируется 1586 годом, т.е. спустя четыре года после исключения Галилея из Пизанского университета.
Физический маятник
Как выглядят колебания и период физического маятника. Узнайте про период колебаний, уравнение и формулу физического маятника, вращательный момент и инерцию.
Период у физического маятника находится в зависимости от момента инерции точки поворота и дистанции к центру масс.
Задача обучения
Основные пункты
Термины
Физический маятник
Простой маятник представлен подвешенным грузом к безмассовой нити или стержню, лишенным трения. Здесь можно не учитывать эффекты от нити. А вот в физическом маятнике нить приобретает вес и способна растягиваться. Тогда период зависит от момента инерции вокруг точки поворота.
Мы видим, как силы влияют сквозь центр масс. Можно вычислить период маятника, выявив момент инерции вокруг точки поворота
Гравитация влияет сквозь центр масс твердого тела. Тогда длина маятника приравнивается к линейной дистанции между осью вращения и центром массы (h).
Уравнение вращательного момента:
τ = Iα (α – угловое ускорение, τ – вращательный момент, I – момент инерции).
Гравитация создает вращательный момент:
τ = mghsinθ (h – дистанция от центра масс к точке поворота, а θ – угол от вертикали).
То есть при небольшом угловом приближении:
Та же форма, что и у обычного простого маятника, где период:
И частота физического маятника:
Если мы располагаем моментом инерции, то можем вычислить период у физического маятника. Рассмотрим однородный стержень, повернутый из рамы. Центр масс расположен на дистанции L/2 от точки подвеса:
Жесткий стержень с равномерным распределением массы свисает с точки поворота. Это пример физического маятника
Момент инерции жесткого стержня вокруг его центра:
Также нужно выявить момент инерции относительно точки поворота, а не центра масс, поэтому применим теорему о параллельной оси:
Добавим результат к уравнению за период:
Только отметьте, что период физического маятника все еще зависит от массы. Зато лишен влияния массового распределения твердого тела. Перемены в форме, размере или распределении массы повлияют и на момент инерции, а это изменит период.
Период колебаний математического маятника
Математический маятник — что это такое
Маятник — твердое тело, которое совершает под действием приложенных сил механические колебания около неподвижной точки или оси.
Простейший маятник состоит из небольшого груза массой m, подвешенного на невесомой нити или тонком стержне длиной l и совершающего колебания под воздействием земного притяжения. Если нить считать нерастяжимой, размер груза незначительным по сравнению с длиной нити, а массу нити незначительной по сравнению с массой груза, то груз можно считать материальной точкой массой m, находящейся на постоянном расстоянии l от точки подвеса. Такой маятник называют математическим.
Определение модели системы
Математические модели динамических систем часто используют для анализа самых разных технических, социально-экономических, естественнонаучных систем, в которых происходят циклические процессы.
Существуют различные классификации динамических процессов. Одна из них изображена на схеме:
Маятник Фуко
Отсюда следует, что если бы Земля не вращалась, данного эффекта просто не существовало бы. Это обстоятельство указывает на то, что причиной неинерциальности земной системы отсчета является вращение планеты.
Центробежное ускорение на экваторе равно 0,034 м/с^2. По сравнению с экваториальным ускорением свободного падения g = 9,78 м/с^2 это величина малая, но она заметно влияет на изменение веса тела на экваторе по сравнению с его весом на полюсе. Если, например, взвешивать на пружинных весах тело массой 10 кг, то уменьшение веса на экваторе за счет действия центробежной силы составит около 35 г.
Период колебаний математического маятника
Период колебаний — время, за которое происходит одно полное колебание. В СИ измеряется в секундах.
Чему равен, от чего зависит частота
Если за время t совершается N колебаний, то период, обозначаемый буквой T, равен
где v — частота колебаний. Она обратно пропорциональна периоду.
Колебания можно изобразить в виде графика:
Источник: physik.ucoz.ru.
Период колебаний математического маятника можно рассчитать по формуле
g — ускорение свободного падения. Не зависит от амплитуды колебаний и массы груза.
В случае математического маятника она определяется длиной подвеса и ускорением свободного падения:
Для физического маятника в уравнение добавляются инерция и масса подвеса:
Для пружинного маятника частоту определяет жесткость пружины k:
Уравнения движения и их решение, формулы с примерами
Математический маятник — это материальная точка, имеющая массу m и подвешенная на нити с неизменяемой длиной l. Покидая положение равновесия, подвес совершает колебательные движения по дуге.
Это дает нам дифференциальное уравнение гармонических колебаний
Из уравнения следует, что при малых углах отклонения от положения равновесия маятник будет колебаться с периодом
Из этого следует, что
Начальная фаза зависит от того, как маятник вывели из положения равновесия. Рассмотрим ситуацию, в которой маятник отклонили от положения равновесия на расстояние А и отпустили без начальной скорости. Запишем уравнение движения колеблющегося тела с учетом того факта, что в начальный момент координата тела будет равна А:
x = A × cos ω t + φ 0 ;
Уравнение движения маятника:
Если маятник толкнули, когда он находился в положении равновесия, начальная координата колеблющейся точки будет равна нулю:
Будет ли начальная координата положительной или отрицательной, определяет выбор положительного направления оси. Если направление оси совпадет с направлением начальной скорости, то в уравнении движения будет знак «плюс», если не совпадет — знак «минус».
Уравнение движения маятника:
Рассмотрим задачи, для которых требуется составлять и решать уравнения движения.
Необходимо определить амплитуду и частоту колебаний точки, если известно, что при смещении точки от положения равновесия на 5 см ее скорость равна 6 см/с, а при смещении на 3 см — 10 см/с.
Исключаем время из системы:
x 1 2 + v 1 2 ω 2 = А 2 x 2 2 + v 2 2 ω 2 = А 2
Преобразовав выражения и подставив значения, данные в условиях задачи, получаем:
Необходимо вычислить циклическую частоту колебаний точки, если известно, что при скорости 13 см/с ускорение равнялось 6 см/с^2, а при уменьшении скорости до 12 см/с произошло увеличение ускорения до 10 см/с^2.
Решение:
Координата точки меняется по закону
Запишем уравнения скорости и ускорения точки:
Преобразуем уравнение, исключив из него А, и подставим значения, данные в условиях задачи:
Практическое применение математического маятника
С помощью математического моделирования динамических систем можно обнаружить схожесть динамических процессов в реальных физических, технических, биологических, химических и социально-экономических системах. Разработка моделей, позволяющих предсказывать время и другие характеристики периодических процессов в этих системах, является эффективным способом анализировать, например, сельскохозяйственные или производственно-экономические процессы.