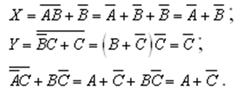Что включают в себя логические выражения
Логическое выражение может включать в себя логические переменные и константы, знаки логических операций, скобки, определяющие порядок выполнения логических операций.
Для формализации логических высказываний будем учитывать следующие положения:
Определение. Логической переменной называется переменная, значением которой может быть любое высказывание.
Существует две логические константы: 0 (ложь) и 1 (истина).
В логических выражениях операции имеют следующий приоритет:
Построение таблицы истинности логического выражения
Для любого логического выражения можно построить таблицу истинности, в которой определяется его истинность или ложность при всех наборах исходных значений логических переменных.
Пример. Построить таблицу истинности для логического выражения: ¬ x ∧ ( y ⇒ z )
При построении таблиц истинности будем использовать следующий алгоритм:
Равносильные логические выражения.
Определение. Формулы А и В, зависящие от одного и того же набора переменных х1 х2, х3, …, хn, называют равносильными или эквивалентными, если на любом наборе значений переменных х1 х2, х3, …, хn они имеют одинаковые значения.
Для обозначения равносильности формул используется знак равенства, например А = В.
Любую формулу можно преобразовать к равносильной ей, в которой используются только базовые логические операции ∧, ∨ и ¬.
Представим через базовый набор эквивалентность:
x ⇔ y = ¬ x ∧ ¬ y ∨ x ∧ y
Докажем равносильность логических формул с помощью построения таблицы истинности.
| x | y | x ⇔ y | ¬ x | ¬ y | ¬ x ∧ ¬ y | x ∧ y | ¬ x ∧ ¬ y ∨ x ∧ y |
|---|---|---|---|---|---|---|---|
| 0 | 0 | 1 | 1 | 1 | 1 | 0 | 1 |
| 0 | 1 | 0 | 1 | 0 | 0 | 0 | 0 |
| 1 | 0 | 0 | 0 | 1 | 0 | 0 | 0 |
| 1 | 1 | 1 | 0 | 0 | 1 | 1 | 1 |
Заметим, что результирующие столбцы в таблице истинности для левой и правой формулы совпали. Таким образом, формулы равносильные.
Copyright © 2014-2021, Урок информатики
Все права защищены
Что включают в себя логические выражения
2) Логическое сложение или дизъюнкция:
Таблица истинности для дизъюнкции
| A | B | F |
| 1 | 1 | 1 |
| 1 | 0 | 1 |
| 0 | 1 | 1 |
| 0 | 0 | 0 |
3) Логическое отрицание или инверсия:
Таблица истинности для инверсии
| A | ¬ А |
| 1 | 0 |
| 0 | 1 |
4) Логическое следование или импликация:
«A → B» истинно, если из А может следовать B.
Обозначение: F = A → B.
Таблица истинности для импликации
| A | B | F |
| 1 | 1 | 1 |
| 1 | 0 | 0 |
| 0 | 1 | 1 |
| 0 | 0 | 1 |
5) Логическая равнозначность или эквивалентность:
Что включают в себя логические выражения

2. Построение таблиц истинности и логических функций.
3. Законы логики и преобразование логических выражений.
Лабораторная работа № 3. Основы математической логики.

Исследования в алгебре логики тесно связаны с изучением высказываний (хотя высказывание — предмет изучения формальной логики). Высказывание — это языковое образование, в отношении которого имеет смысл говорить о его истинности или ложности (Аристотель).
Простым высказыванием называют повествовательное предложение, относительно которого имеет смысл говорить, истинно оно или ложно.
Считается, что каждое высказывание либо истинно, либо ложно и ни одно высказывание не может быть одновременно истинным и ложным.
Высказывания 1 и 3 являются истинными. Высказывание 2 – ложным , потому что число 27 составное 27=3*3*3.
Итак, отличительным признаком высказывания является свойство быть истинным или ложным, последние четыре предложения этим свойством не обладают.
С помощью высказываний устанавливаются свойства, взаимосвязи между объектами. Высказывание истинно, если оно адекватно отображает эту связь, в противном случае оно ложно.
Однако определение истинности высказывания далеко не простой вопрос. Например, высказывание «Число 1 +22 = 4294 967297 — простое», принадлежащее Ферма (1601-1665), долгое время считалось истинным, пока в 1732 году Эйлер (1707-1783) не доказал, что оно ложно. В целом, обоснование истинности или ложности простых высказываний решается вне алгебры логики. Например, истинность или ложность высказывания «Сумма углов треугольника равна 180°» устанавливается геометрией, причем в геометрии Евклида это высказывание является истинным, а в геометрии Лобачевского — ложным.
В булевой алгебре простым высказываниям ставятся в соответствие логические переменные, значение которых равно 1, если высказывание истинно, и 0, если высказывание ложно. Обозначаются логические переменные, большими буквами латинского алфавита.
Существуют разные варианты обозначения истинности и ложности логических переменных:
Сложные (составные) высказывания представляют собой набор простых высказываний (по крайней мере двух) связанных логическими операциями.
С помощью логических переменных и символов логических операций любое высказывание можно формализовать, то есть заменить логической формулой (логическим выражением).
Связки «НЕ», «И», «ИЛИ» заменяются логическими операциями инверсия, конъюнкция, дизъюнкция. Это основные логические операции, при помощи которых можно записать любое логическое выражение.
Введем перечисленные логические операции.
В алгебре множеств конъюнкции соответствует операция пересечения множеств, т.е. множеству получившемуся в результате умножения множеств А и В соответствует множество, состоящее из элементов, принадлежащих одновременно двум множествам.
Логические выражения и логические операции



Исследования в алгебре логики тесно связаны с изучением высказываний (хотя высказывание — предмет изучения формальной логики).
Высказывание — это языковое образование, в отношении которого имеет смысл говорить о его истинности или ложности (Аристотель).
Простым высказыванием называют повествовательное предложение, относительно которого имеет смысл говорить, истинно оно или ложно.
Считается, что каждое высказывание либо истинно, либо ложно и ни одно высказывание не может быть одновременно истинным и ложным.
Примеры высказываний:
1. Москва – столица России.
2. Число 27 является простым.
3. Волга впадает в Каспийское море.
Высказывания 1 и 3 являются истинными. Высказывание 2 – ложным , потому что число 27 составное 27 = 3*3*3.
Следующие предложения высказываниями не являются:
Отличительным признаком высказывания является свойство быть истинным или ложным, последние четыре предложения этим свойством не обладают.
С помощью высказываний устанавливаются свойства, взаимосвязи между объектами. Высказывание истинно, если оно адекватно отображает эту связь, в противном случае оно ложно.
Примеры высказываний:
1. Сегодня светит солнце.
В целом, обоснование истинности или ложности простых высказываний решается вне алгебры логики. Например, истинность или ложность высказывания «Сумма углов треугольника равна 180°» устанавливается геометрией, причем в геометрии Евклида это высказывание является истинным, а в геометрии Лобачевского — ложным.
В булевой алгебре простым высказываниям ставятся в соответствие логические переменные, значение которых равно 1, если высказывание истинно, и 0, если высказывание ложно. Обозначаются логические переменные, большими буквами латинского алфавита.
Существуют разные варианты обозначения истинности и ложности логических переменных:
| Истина | И | True | T |
| Ложь | Л | False | F |
Сложные (составные) высказывания представляют собой набор простых высказываний (по крайней мере двух) связанных логическими операциями.
С помощью логических переменных и символов логических операций любое высказывание можно формализовать, то есть заменить логической формулой (логическим выражением).
Введем перечисленные логические операции.
В алгебре множеств конъюнкции соответствует операция пересечения множеств, т.е. множеству получившемуся в результате умножения множеств А и В соответствует множество, состоящее из элементов, принадлежащих одновременно двум множествам.
| Таблица истинности | Диаграмма Эйлера-Венна | |||
| 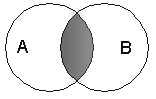 |
Если два высказывания соединены союзом «И», то полученное сложное высказывание истинно тогда и только тогда, когда истинны оба исходных высказывания.
В алгебре множеств дизъюнкции соответствует операция объединения множеств, т.е. множеству получившемуся в результате сложения множеств А и В соответствует множество, состоящее из элементов, принадлежащих либо множеству А, либо множеству В.
| Таблица истинности | Диаграмма Эйлера-Венна | |||
| 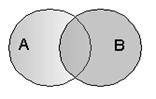 |
Если два высказывания соединены союзом «ИЛИ», то полученное сложное высказывание истинно когда истинно хотя бы одно из составляющих высказываний.
Рассмотренные выше операции были двуместными (бинарными), т.е. выполнялись над двумя операндами (высказываниями). В алгебре логики определена и широко используется и одноместная (унарная) операция отрицание.
В алгебре множеств логическому отрицанию соответствует операция дополнения до универсального множества, т.е. множеству получившемуся в результате отрицания множества А соответствует множество, дополняющее его до универсального множества.
| Таблица истинности | Диаграмма Эйлера-Венна | ||
| 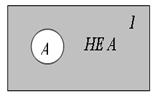 |
Если исходное выражение истинно, то результат отрицания будет ложным, и наоборот, если исходное выражение ложно, то результат отрицания будет истинным.
Логическое следование (импликация):
A => B
«Из А следует В»
«А равносильно В»
Новое высказывание, полученное с использованием эквивалентности, является истинным тогда и только тогда, когда оба исходных высказывания одновременно истинны или одновременно ложны.
В алгебре логики логические связки и соответствующие им логические операции имеют специальные названия и обозначаются следующим образом:
Примеры записи сложных высказываний с помощью обозначения логических связок:
2. «Если хочешь быть красивым, поступи в гусары.» (К. Прутков) А => В
Построение таблиц истинности и логических функций
Порядок выполнения логических операций в сложном логическом выражении:
Для изменения указанного порядка выполнения операций используются скобки.
Алгоритм построения таблиц истинности для сложных выражений:
1. Определить количество строк:
количество строк = 2 n + строка для заголовка,
2. Определить количество столбцов:
количество столбцов = количество переменных + количество логических операций;
— определить количество переменных (простых выражений);
— определить количество логических операций и последовательность их выполнения.
3. Заполнить столбцы результатами выполнения логических операций в обозначенной последовательности с учетом таблиц истинности основных логических операций.
Пример: Составить таблицу истинности логического выражения:
D = А & (B Ú C).
1. Определить количество строк:
на входе три простых высказывания: А, В, С поэтому n = 3 и количество строк = 2 3 +1 = 9.
2. Определить количество столбцов:
— простые выражения (переменные): А, В, С;
— промежуточные результаты (логические операции):
А — инверсия (обозначим через E);
B Ú C — операция дизъюнкции (обозначим через F);
а также искомое окончательное значение арифметического выражения:
D = А & (B Ú C). т.е. D = E & F — это операция конъюнкции.
3. Заполнить столбцы с учетом таблиц истинности логических операций.
Построение логической функции по ее таблице истинности:
Попробуем решить обратную задачу. Пусть дана таблица истинности для некоторой логической функции:
Составить логическую функцию для заданной таблицы истинности.
Правила построения логической функции по ее таблице истинности:
1. Выделить в таблице истинности те строки, в которых значение функции равно 1.
2. Выписать искомую формулу в виде дизъюнкции нескольких логических элементов. Число этих элементов равно числу выделенных строк.
3. Каждый логический элемент в этой дизъюнкции записать в виде конъюнкции аргументов функции.
4. Если значение какого-либо аргумента функции в соответствующей строке таблице равно 0, то этот аргумент взять с отрицанием.
1. В первой и третьей строках таблицы истинности значение функции равно 1.
2. Так как строки две, получаем дизъюнкцию двух элементов: ( ) V ( ).
3. Каждый логический элемент в этой дизъюнкции запишим в виде конъюнкции аргументов функции X и Y: (X & Y) V (X & Y).
4. Берем аргумент с отрицанием если его значение в соответствующей строке таблицы равно 0 и получаем искомую функцию:
Z (X, Y) =( X & Y) V (X & Y).
Законы логики и правила преобразования логических выражений
1. Закон двойного отрицания (двойное отрицание исключает отрицание):
А = 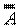
2. Переместительный (коммутативный) закон:
— для логического сложения: А Ú B = B Ú A;
— для логического умножения: A & B = B & A.
Результат операции над высказываниями не зависит от того, в каком порядке берутся эти высказывания.
3. Сочетательный (ассоциативный) закон:
— для логического сложения: (А Ú B) Ú C = A Ú (B Ú C);
— для логического умножения: (A & B) & C = A & (B & C).
При одинаковых знаках скобки можно ставить произвольно или вообще опускать.
4. Распределительный (дистрибутивный) закон:
— для логического умножения: (A & B) Ú C = (A Ú C) & (B Ú C).
Закон определяет правило выноса общего высказывания за скобку.
— для логического сложения: 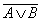
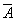
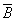
— для логического умножения: 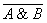
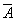
6. Закон идемпотентности (от латинских слов idem — тот же самый и potens — сильный; дословно — равносильный):
— для логического сложения: А Ú A = A;
— для логического умножения: A & A = A .
Закон означает отсутствие показателей степени.
7. Законы исключения констант:
— для логического сложения: А Ú 1 = 1, А Ú 0 = A;
— для логического умножения: A & 1 = A, A & 0 = 0.
— A & 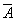
Невозможно, чтобы противоречащие высказывания были одновременно истинными.
— A Ú 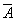
Из двух противоречащих высказываний об одном и том же предмете одно всегда истинно, а второе — ложно, третьего не дано.
10. Закон поглощения:
— для логического умножения: A & (A Ú B) = A.
Знание законов логики позволяет проверять правильность рассуждений и доказательств. Основываясь на законах, можно выполнять упрощение сложных логических выражений. Такой процесс замены сложной логической функции более простой, но равносильной ей, называется минимизацией функции.
Нарушения законов логики приводят к логическим ошибкам и вытекающим из них противоречиям.
Упрощение формул.
Пример 1. Упростить формулу (А Ú В) & (А Ú С).
4. Аналогично предыдущему пункту вынесем за скобки высказывание А. A Ú B & A Ú B & C = A & (1 Ú B) Ú B & C = A Ú B & C.
Таким образом, мы доказали закон дистрибутивности.
Пример 2. Упростить выражения 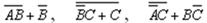
Решение :
Учитель информатики
Сайт учителя информатики. Технологические карты уроков, Подготовка к ОГЭ и ЕГЭ, полезный материал и многое другое.
Логические выражения.
Информатика. Учебник для 9 класса (по учебнику К. Ю. Полякова, Е.А. Еремина, базовый уровень)
§11. Логические выражения.
Формализация
Ключевые слова:
Обозначив простые высказывания буквами — логическими переменными и используя логические операции, можно записать любое высказывание в виде логического выражения.
Логическое выражение — это выражение, результат вычисления которого — логическое значение (истина или ложь).
Например, пусть система сигнализации должна дать аварийный сигнал, если вышли из строя два из трёх двигателей самолёта. Обозначим высказывания:
А = Первый двигатель вышел из строя;
В = Второй двигатель вышел из строя;
С = Третий двигатель вышел из строя;
X = Аварийная ситуация.
Тогда логическое высказывание X можно записать в виде логического выражения (логической формулы):
X = (А и В) или (А и С) или (В и С).
Это выражение может быть записано с помощью других обозначений:
X = (А • В) + (А • С) + (В • С). (*)
Таким образом, мы выполнили формализацию.
Формализация — это переход от конкретного содержания высказываний к записи с помощью формального языка.
При вычислении логических выражений установлен такой порядок выполнения операций:
1) действия в скобках;
2) отрицание (НЕ);
3) логическое умножение (И), слева направо;
4) логическое сложение (ИЛИ), слева направо.
Можно ли убрать скобки в выражении (*)? Почему?
Уберите лишние скобки в логических выражениях:
а) X = (А + (В • С) • (А + С));
б) X = (А + B) • (C • А) • (А + (B + C))).
Вычислите значение логического выражения X = (А • В + С) • (А + C) при:
а) А = О, В = О, С = 1;
б) А = О, В = 1, С = 1;
в) А = 1, В = 1, С = 0.
Таблицы истинности
Любую логическую функцию можно задать с помощью таблицы истинности, которая показывает, чему равно значение логического выражения при всех возможных комбинациях значений исходных переменных. Построим таблицу истинности для выражения
X = А и не В или не А и B,
которое можно также записать в виде
Сколько строк в таблице истинности выражения с двумя переменными?
Будем вычислять выражение по частям: добавим в таблицу истинности дополнительные столбцы А • B и А • В, а потом выполним операцию ИЛИ с этими значениями (рис. 2.18).
Рис. 2.18
Из этой таблицы истинности видно, что при некоторых значениях переменных значение X истинно, а при некоторых — ложно. Такие выражения называют вычислимыми.
Высказывание «Вася — школьник или он не учится в школе» всегда истинно (для любого Васи). Выражение, истинное при любых значениях переменных, называется тождественно истинным или тавтологией.
Высказывание «Сегодня безветрие, и дует сильный ветер» никогда не может быть истинным. Соответствующее логическое выражение всегда ложно, оно называется тождественно ложным или противоречием.
Выполните формализацию высказываний, о которых шла речь в последних двух абзацах. Запишите формулы для упрощения каждого из них.
Постройте самостоятельна таблицу истинности логического выражения X = (А + В) • (A + B). Сравните её с таблицей на рис. 2.18. Истинно ли высказывание «Разные логические выражения могут определять одну и ту же логическую функцию»?
Если два выражения принимают одинаковые значения при всех значениях переменных, они называются равносильными или тождественно равными. Равносильные выражения определяют одну и ту же логическую функцию, т. е. при одинаковых исходных данных приводят к одинаковым результатам.
Сколько строк в таблице истинности выражения с тремя переменными?
Постройте таблицу истинности логического выражения
Х = А • В + А • С + В • С.
Предположим, что нам известна только часть таблицы истинности для функции трёх переменных (рис. 2.19).
Рис. 2.19
Как вы думаете, можно ли по такой части таблицы истинности определить логическую функцию? Почему?
Всего в таблице истинности функции от трёх переменных 2 3 = 8 строк, для каждой из них нужно знать, чему равно значение функции. В нашем примере пять значений функции неизвестны, причём каждое из них может быть равно 0 или 1, т. е. у нас есть 5 свободных бит.
Сколько различных значений можно закодировать с помощью 5 бит?
Как вы нашли это значение?
Итак, таблице на рис. 2.19 могут соответствовать 32 различные логические функции. Проверим, подходят ли следующие варианты:
Прежде всего, заметим, что в столбце значений функции два нуля и одна единица. Следовательно, вариант а) не подходит, потому что цепочка операций ИЛИ со всеми переменными (или их инверсиями, обратными значениями) даст только один ноль — в случае, когда все слагаемые равны нулю.
Проверяем вариант б), подставляя значения переменных А, В и С сначала из первой строки таблицы, потом из второй и третьей. В первой строке получаем A • С + В = 1 • 1 + 0 = 1, этот результат совпадает со значением функции в этой строке. Для второй строки A • С + В = 1 • 1 + 1 = 1, значит, эта функция тоже не подходит.
Проверьте самостоятельно, подходят ли остальные варианты.
Скажите без вычислений, сколько нулей и сколько единиц должно быть в последнем столбце таблицы истинности функций с тремя переменными:
Теперь предположим, что нам известна часть таблицы какой-то логической функции, причём с пропусками (рис. 2.20).
Рис. 2.20
Выясним, какие из следующих функций могут соответствовать этой таблице:
Во-первых, обратим внимание, что в столбце значений функции две единицы, поэтому сразу делаем вывод, что это не могут быть цепочки двух операций И (ответы б) и г) неверные). Остались три цепочки из операций ИЛИ, причём для верхней строки (при А = 0 и С = 1) мы должны получить 0 при каком-то выборе неизвестного значения В. Подставляем А = 0 и С = 1 в формулы-кандидаты:
Видим, что в случае а) сумма не может быть равна нулю, это неверный ответ. А варианты в) и д) подходят: в первом из них нужно в первой строке поставить в пустую ячейку 1, а во втором — 0.
Кратко решение можно записать так:
1) поскольку в столбце значений функции один ноль, это не может быть цепочка операций И; остаются только цепочки операций ИЛИ;
2) для того чтобы получить нулевое значение функции в первой строке таблицы, нужно, чтобы переменная А (равная 0 в этой строке) входила в логическую сумму без инверсии (к ней не должна применяться операция НЕ) а переменная С (равная 1) — с инверсией;
3) этим условиям удовлетворяют функции в) и д).
Известна часть таблицы какой-то логической функции с пропусками (рис. 2.21).
Рис. 2.21
Выясните, какие из следующих функций могут соответствовать этой таблице:
Составление условий
Логические выражения часто используются при решении математических задач с помощью компьютеров.
Построим условия (логические выражения), соответствующие заштрихованным областям на числовой оси (рис. 2.22).
Рис. 2.22
На рисунке 2.22, а выделен отрезок [3; 6]. Для того чтобы определить такую область, нужно ограничить значение х с двух сторон: оно должно быть больше или равно трём и меньше или равно шести, причем эти два условия должны выполняться одновременно, т. е. их нужно связать с помощью операции И:
Область на рис. 2.22, б — это объединение двух отрезков. Мы можем отдельно записать условия для каждого отрезка и связать их с помощью операции ИЛИ:
Запишите условие, которое определяет область на рис. 2.22, в.
Теперь рассмотрим задачу с областью на плоскости. Запишем условие, соответствующее заштрихованной части (рис. 2.23).
Рис. 2.23
Требуется составить логическое выражение, зависящее от переменных х и у, которое будет равно 1 (истинно) внутри заштрихованной области и равно 0 вне её.
Рис. 2.24
Запишите условие, которое определяет области на рисунках (рис. 2.25).
Рис. 2.25
Построим логическое выражение для области на рис. 2.26.
Рис. 2.26
Можно разделить заштрихованную область на две части (рис. 2.27).
а вторая — выражением
Поскольку нам нужно «сложить» две области, эти выражения нужно объединить с помощью операции логического сложения (ИЛИ):
Попробуйте ещё упростить полученное условие.
Запишите условие, которое определяет области на рисунках (рис. 2.28).
Рис. 2.28
Логические схемы
Вернёмся снова к примеру с системой аварийной сигнализации самолёта. Предположим, что на каждом двигателе установлен логический датчик, который выдаёт условный сигнал 1 (например, высокий уровень напряжения), если двигатель неисправен, и условный сигнал 0, если двигатель исправен. Требуется построить логическую схему — схему логического устройства, — которая при аварии выдаёт условный сигнал 1, а в режиме нормальной работы — сигнал 0.
Сигналы от трёх двигателей назовём А, Б и С. В начале параграфа мы уже составили логическое выражение для запуска аварийной сигнализации:
Х = А • В + А • С + В • С.
Здесь три логических умножения и два логических сложения. Сначала выполняются все операции умножения (слева направо), а затем — все операции сложения (тоже слева направо). Расставим номера операций:
| 1 | 4 | 2 | 5 | 3 | ||||||||
| Х | = | А | • | В | + | А | • | С | + | В | • | С. |
Последней выполняется вторая операция сложения. Поэтому последний элемент в схеме — это элемент логического сложения ИЛИ (рис. 2.29).
Рис. 2.29
На первый вход этого элемента ИЛИ подаётся сигнал А • В + А • С, в этом выражении последняя операция — логическое сложение, добавляем ещё один элемент ИЛИ (рис. 2.30).
Рис. 2.30
Три операции логического умножения добавляют в схему три элемента И (рис. 2.31).
Рис. 2.31
Запишите в тетради логическое выражение по логической схеме (рис. 2.32).
Рис. 2.32
Постройте логическую схему, соответствующую выражению:
в) Z = A • B + A • B • C.
Работа в парах. Один из вас пусть нарисует логическую схему для выражения X = A + В • С (черта сверху обозначает, что операция отрицания применяется ко всему выражению), а второй — для выражения Y = (А + В) (А + С). Постройте таблицы истинности для своих выражений и сравните их. Какую формулу вы сейчас вместе доказали?
Работа в парах. Запишите логическое выражение, включающее 5-6 операций, и предложите соседу нарисовать логическую схему. Проверьте и обсудите с ним его решение.
Путешествуя по Зазеркалью, Алиса увидела дверь с тремя кнопками, которые были отмечены буквами А, В и С. На двери висела схема (рис. 2.33).
Рис. 2.33
На какую (одну!) из трёх кнопок нужно нажать Алисе, чтобы открыть дверь?
Выводы
• Формализация — это переход от конкретного содержания высказываний к записи с помощью формального языка.
• В логических выражениях операции выполняются в следующем порядке:
1) действия в скобках;
2) отрицание (НЕ);
3) логическое умножение (И), слева направо;
4) логическое сложение (ИЛИ), слева направо.
Для изменения порядка действий используются скобки.
• Таблица истинности логического выражения показывает, чему равно значение выражения при всех возможных комбинациях значений исходных переменных.
• Логические выражения, истинность которых зависит от значений исходных переменных, называют вычислимыми.
• Логическое выражение, которое всегда истинно, называется тождественно истинным или тавтологией. Выражение, которое всегда ложно, называют тождественно ложным или противоречием. Пример тождественно истинного выражения: А + А, пример тождественно ложного: А • А.
• Два выражения, принимающие одинаковые значения при всех значениях переменных, называются равносильными или тождественно равными. Равносильные выражения определяют одну и ту же логическую функцию.
Нарисуйте в тетради интеллект-карту этого параграфа.
Вопросы и задания
1. Что можно сделать для того, чтобы изменить порядок выполнения действий в логических выражениях?
2. Поясните разницу между терминами «логическое выражение» и «логическая функция».
3. Как можно доказать (или опровергнуть) логическую формулу?
4. Можно ли сказать, что таблица истинности однозначно определяет:
а) логическое выражение;
б) логическую функцию?
5. Что такое вычислимое логическое выражение?
6. Что такое равносильные выражения?
7. Выполните по указанию учителя задания в рабочей тетради.