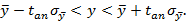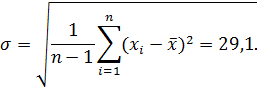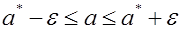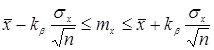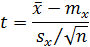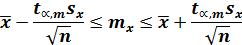чем больше доверительная вероятность тем
Доверительные вероятности и уровни значимости.



По выборочным характеристикам можно построить интервал, в котором с той или иной вероятностью находится генеральный параметр. Вероятности, признанные достаточными для уверенного суждения о генеральных параметрах на основании выборочных показателей, называют доверительными.
Понятие о доверительных вероятностях вытекает из принципа, что маловероятные события считаются практически невозможными, а события, вероятность которых близка к единице, принимают за почти достоверные. Обычно в качестве доверительных используют вероятности Р1 = 0.95, Р2 = 0.99, Р3 = 0.999. Определенным значениям вероятностей соответствуют уровни значимости, под которыми понимают разность α = 1–Р. Вероятности 0.95 соответствует уровень значимости α1= 0.05 (5%), вероятности 0.99 – α2 = 0.01 (1%), вероятности 0.999 – α3 = 0.001 (0.1%).
Это означает, что при оценке генеральных параметров по выборочным показателям существует риск ошибиться в первом случае 1 раз на 20 испытаний, т.е. в 5% случаев; во втором – 1 раз на 100 испытаний, т.е. в 1% случаев; в третьем – 1 раз на 1000 испытаний, т.е. в 0.1% случаев. Таким образом, уровень значимости обозначает вероятность получения случайного отклонения от установленных с определенной вероятностью результатов. Вероятности, принятые как доверительные, определяют доверительный интервал между ними. На них можно основывать оценку той или иной величины и те границы, в которых она может находиться при разных вероятностях.
Для различных вероятностей доверительные интервалы будут следующими:
— Р1 = 0.95 интервал – 1.96σ до + 1.96σ (рис. 5)
— Р2 = 0.99 интервал – 2.58σ до + 2.58σ
— Р3 = 0.999 интервал – 3.03σ до + 3.03σ
Доверительным вероятностям соответствуют следующие величины нормированных отклонений:
— вероятности Р1 = 0.95 соответствует t1 = 1.96σ
— вероятности Р2 = 0.99 соответствует t2 = 2.58σ
— вероятности Р3 = 0.999 соответствует t3 = 3.03σ
Выбор того или иного порога доверительной вероятности осуществляют исходя из важности события. Уровень значимости в таком случае – эта та вероятность, которой решено пренебрегать в данной исследовании или явлении.
Средняя ошибка  (m), или ошибка репрезентативности.
(m), или ошибка репрезентативности.
Выборочные характеристика, как правило, не совпадают по абсолютной величине с соответствующими генеральными параметрами. Величину отклонения выборочного показателя от его генерального параметра называют статистической ошибкой, или ошибкой репрезентативности. Статистические ошибки присущи только выборочным характеристикам, они возникают в процессе отбора вариант из генеральной совокупности.
Средняя ошибка вычисляется по формуле:
(5) 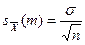
где σ – среднее квадратическое отклонение,
n – количество измерений (объем выборки).
Выражается в тех же единицах измерения, что и 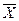
Величина средней ошибки обратно пропорциональна численности выборочной совокупности. Чем больше размеры выборки, тем меньше средняя ошибка, а следовательно, меньше расхождение между значениями признаков в выборочных и генеральной совокупностях.
Среднюю ошибку выборки можно использовать для оценки генеральной средней согласно закону нормального распределения. Так, в пределах ±1 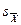
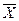
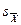
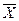
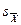
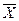
Поэтому, зная среднюю арифметическую выборки 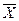
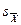
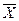
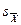
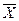
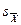
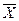
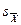
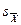
Теория выборочного метода
| Главная > Учебные материалы > Математика: Теория выборочного метода | |||
 | |||
 | |||
| 1.Выборочный метод. 2.Оценка параметров выборочной совокупности. 3.Доверительная вероятность. Предельная ошибка выборки. | |||
1.Выборочный метод.
Одним из недостатков, который возникает при использовании выборочного метода, является ошибка репрезентативности. Данная ошибка возникает по причине того, что исследуется не вся совокупность, а выборочная.
Критерий, который должен соблюдаться при отборе объектов для изучения, является случайность. Иными словами, все объекты, отобранные для обследования, должны случайным образом попасть в выборочную совокупность. В противном случае результаты могут оказаться ложными.
Для отбора объектов, которые должны будут подвергнуты изучению, обычно используют один из двух способов образования выборки. Первый способ предусматривает возвращение объекта обследования в общую совокупность после его изучения. Второй способ предусматривает, что отобранный объект не будет возвращен в общую совокупность после его изучения.
Числовые характеристики выборочной совокупности называются соответственно выборочными. Основные характеристики:
Основной задачей выборочного метода наблюдений заключается в том, что бы оценить характеристики генеральной совокупности объектов исследования по данным выборочной совокупности.
2.Оценка параметров выборочной совокупности.
Пусть задана генеральная совокупность объектов исследования. Число объектов генеральной совокупности равно N. Число N имеет большое значение и исследовать всю совокупность не представляется возможным. По этой причине исследуют выборочную совокупность. И параметр 

Например, пусть параметр θ является математическим ожиданием случайной величины Х. Тогда оценкой 
Свойства оценок. Основными свойствами оценок является несмещенность, состоятельность и эффективность.
Несмещенность оценки означает ее отклонение от этого же параметра генеральной совокупности, т.е. математическое ожидание этой оценки равно оцениваемому параметру.
Если это равенство не выполняется, то полученная оценка является завышенной или заниженной.
Состоятельность означает приближение оценки к оцениваемому параметру при стремлении n к бесконечности. Или сходимость по вероятности к параметру генеральной совокупности.
Отсюда можно сделать вывод, что чем больше выборка n, тем точнее оцениваемый параметр.
Эффективной оценкой параметра θ называется такая несмещенная оценка 

3.Доверительная вероятность. Предельная ошибка выборки.
При исследовании выборочной совокупности рассчитанная средняя арифметическая может иметь некоторое отклонение от средней арифметической генеральной совокупности. Это отклонение называется ошибкой репрезентативности, которая возникает по причине исследования не всей, а выборочной совокупности. Наибольшее отклонение выборочной средней от средней арифметической генеральной совокупности, которое возможно при заданной доверительной вероятности называется предельной ошибкой выборки.
Построение доверительного интервала для генеральной средней по большой выборке.
Доверительный интервал для генеральной средней при n порядка нескольких сотен рассчитывается по следующей формуле:
переменная t равна:
Отсюда следует, что при заданной доверительной вероятности γ предельная ошибка выборочной средней равна произведению t (значение функции Лапласа) и средней квадратической ошибки.
Доверительный интервал генеральной средней рассчитывается по формуле:
Для нахождения предельной ошибки Δ необходимо найти среднюю квадратическую ошибку. Средняя квадратическая ошибка рассчитывается по следующей формуле:
При достаточно большом объеме выборки n выборочная дисперсия приближается к генеральной дисперсии, поэтому чем больше n, тем точнее значение средней квадратической ошибки.
Построение доверительного интервала для генеральной доли по большой выборке.
Если распределение выборочной доли w считать приблизительно нормальным, то для нахождения доверительного интервала для генеральной доли используем формулу предельную ошибки:
Из графика (рис.2) можно увидеть, что доверительный интервал находится внутри эллипса между значениями p1 и p2. И чем больше объем выборки n, тем эллипс становится более вытянутым и доверительный интервал становится более узким.
Можно вспомнить, что и дисперсия случайной величины, которая равна D(X) = npq для биномиального распределения, так же имеет максимальное значение в этой точке.
Пример.
В коммерческом банке из 5000 вкладов отобраны 792, которые распределены по группам в зависимости от их величины. Распределение вкладов имеет показательный закон распределения. Данные представлены в таблице.

Необходимо найти вероятность того, что средний размер вклада отличается от выборочной средней не более, чем 20 д.е. по абсолютной величине и найти так же границы, в которых с вероятностью 0.99 заключен средний размер вклада. Данные величины найти для повторной и бесповторной выборки. Найти вероятность того, что размер вклада будет заключен в пределах от 600 до 1000 д.е.
Решение.
Найдем выборочную среднюю арифметическую и выборочную дисперсию и построим гистограмму распределения частот.



Найдем границы, в которых с вероятностью 0.99 заключен средний размер вклада.

Найдем вероятность того, что размер вклада будет заключен в пределах от 600 до 1000 д.е.
Доверительная вероятность и доверительный интервал.
Вероятность того, что истинное значение измеряемой величины лежит внутри некоторого интервала, называется доверительной вероятностью, или коэффициентом надежности,а сам интервал — доверительным интервалом.
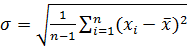
на так называемый коэффициент Стьюдента. Коэффициенты Стьюдента 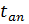
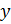
| Число измерений n | Доверительная вероятность y | ||
| 0,67 | 0,90 | 0,95 | 0,99 |
| 2,0 | 6,3 | 12,7 | 63,7 |
| 1,3 | 2,4 | 3,2 | 5,8 |
| 1,2 | 2,1 | 2,8 | 4,6 |
| 1,2 | 2,0 | 2,6 | 4,0 |
| 1,1 | 1,8 | 2,3 | 3,3 |
| 1,0 | 1,7 | 2,0 | 2,6 |
Окончательно, для измеряемой величины y при заданной доверительной вероятности y и числе измерений n получается условие
Величину 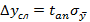
Пример: см. лекцию №5 – ряд чисел.
При числе измерений – 45 и доверительной вероятности – 0,95 получим, что коэффициент Стьюдента приблизительно равен 2,15. Тогда доверительный интервал для данного ряда измерений равен 62,6.
Источником грубых погрешностей нередко бывают резкие изменения условий измерения и ошибки, допущенные оператором:
— неправильный отсчет по шкале измерительного прибора, происходящий из-за неверного учета цены малых делений шкалы;
— неправильная запись результата наблюдений, значений отдельных мер использованного набора, например, гирь;
— хаотические изменения параметров напряжения, питающего средства измерения, например, его амплитуды или частоты.
Доверительный интервал. Азбука медицинской статистики. Глава III
Константин Кравчик доходчиво объясняет, что такое доверительный интервал в медицинских исследованиях и как его использовать
«Катрен-Стиль» продолжает публикацию цикла Константина Кравчика о медицинской статистике. В двух предыдущих статьях автор касался объяснения таких понятий, как размер выборки, генеральная совокупность, статистическая гипотеза и классификацию шкал.
Математик-аналитик. Специалист в области статистических исследований в медицине и гуманитарных науках
Очень часто в статьях по клиническим исследованиям можно встретить загадочное словосочетание: «доверительный интервал» (95 % ДИ или 95 % CI — confidence interval). Например, в статье может быть написано: «Для оценки значимости различий использовали t-критерий Стьюдента с расчетом 95 % доверительного интервала».
Какого же значение «95 % доверительного интервала» и зачем его рассчитывать?
Что такое доверительный интервал? — Это диапазон, в котором находятся истинные средние значения в генеральной совокупности. А что, бывают «неистинные» средние значения? В каком‑то смысле да, бывают. В прошлой статье мы объясняли, что невозможно измерить интересующий параметр во всей генеральной совокупности, поэтому исследователи довольствуются ограниченной выборкой. В этой выборке (например, по массе тела) есть одно среднее значение (определенный вес), по которому мы и судим о среднем значении во всей генеральной совокупности. Однако едва ли средний вес в выборке (особенно небольшой) совпадет со средним весом в генеральной совокупности. Поэтому более правильно рассчитывать и пользоваться диапазоном средних значений генеральной совокупности.
Например, представим, что 95 % доверительный интервал (95 % ДИ) по гемоглобину составляет от 110 до 122 г/л. Это означает, что с вероятностью 95 % истинное среднее значение по гемоглобину в генеральной совокупности будет находиться в пределах от 110 до 122 г/л. Иными словами, мы не знаем средний показатель гемоглобина в генеральной совокупности, но можем с 95 %-й вероятностью указать диапазон значений для этого признака.
Доверительный интервал особенно уместен для разницы в средних значениях между группами или, как это называют, в размере эффекта.
Допустим, мы сравнивали эффективность двух препаратов железа: давно присутствующего на рынке и только что зарегистрированного. После курса терапии оценили концентрацию гемоглобина в исследуемых группах пациентов, и статистическая программа нам посчитала, что разность между средними значениями двух групп с вероятностью 95 % находится в диапазоне от 1,72 до 14,36 г/л (табл. 1).
Табл. 1. Критерий для независимых выборок
(сравниваются группы по уровню гемоглобина)
| t-критерий | Значимость (2-сторонняя) | Разность средних | 95 % доверительный интервал для разности | |
| 2,609 | 0,014 | 8,048 | 1,7274 | 14,3678 |
Трактовать это следует так: у части пациентов генеральной совокупности, которая принимает новый препарат, гемоглобин будет выше в среднем на 1,72–14,36 г/л, чем у тех, кто принимал уже известный препарат.
Иными словами, в генеральной совокупности разность в средних значениях по гемоглобину у групп с 95 %-й вероятностью находится в этих пределах. Судить, много это или мало, будет уже исследователь. Смысл всего этого в том, что мы работаем не с одним средним значением, а с диапазоном значений, следовательно, мы более достоверно оцениваем разницу по параметру между группами.
В статистических пакетах, на усмотрение исследователя, можно самостоятельно сужать или расширять границы доверительного интервала. Снижая вероятности доверительного интервала, мы сужаем диапазон средних. Например, при 90 % ДИ диапазон средних (или разницы средних) будет уже, чем при 95 %.
И наоборот, увеличение вероятности до 99 % расширяет диапазон значений. При сравнении групп нижняя граница ДИ может пересечь нулевую отметку. Например, если мы расширили границы доверительного интервала до 99 %, то границы интервала расположились от –1 до 16 г/л. Это означает, что в генеральной совокупности есть группы, различие средних между которыми по изучаемому признаку равняется 0 (М=0).
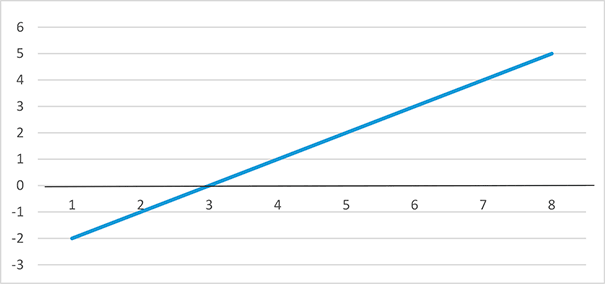
Почему рекомендуется смотреть на доверительный интервал? Для большей наглядности обратимся к рисунку.
95% доверительный интервал разницы по гемоглобину, (г/л)
На рисунке в виде линии изображен 95 % доверительный интервал разницы средних значений по гемоглобину между двумя группами. Линия проходит нулевую отметку, следовательно, имеет место разница между средними значениями, равная нулю, что подтверждает нулевую гипотезу о том, что группы не различаются. Диапазон разницы между группами лежит от –2 до 5 г/л, Это означает, что гемоглобин может как снизиться на 2 г/л, так и повыситься на 5 г/л.
Доверительный интервал — очень важный показатель. Благодаря ему можно посмотреть, были ли различия в группах действительно за счет разности средних или за счет большой выборки, т. к. при большой выборке шансы найти различия больше, чем при малой.
На практике это может выглядеть так. Мы взяли выборку в 1000 человек, измерили уровень гемоглобина и обнаружили, что доверительный интервал разницы средних лежит от 1,2 до 1,5 г/л. Уровень статистической значимости при этом p 22539 просмотров
Нашли ошибку? Выделите текст и нажмите Ctrl+Enter.
Доверительные интервалы и доверительная вероятность
Точечные оценки имеют тот недостаток, что по ним нельзя судить о точности полученных оценок. Поэтому возникает задача определения на основании выборочных значений такого интервала, который покрывал бы неизвестной значение параметра с заданной вероятностью.
В отличие от точечной оценки, интервальная оценка позволяет получить вероятностную характеристику точности оцениваемого параметра.
Выборочные параметры являются случайными величинами, их отклонения от генеральных (т.е. погрешности их определения) также будут случайными. Оценка этих отклонений носит вероятностный характер – можно лишь указать вероятность той или иной погрешности. Для этого в математической статистике пользуются доверительными интервалами и доверительными вероятностями.
Доверительный интервал – интервал, который с заданной вероятностью накроет неизвестное значение оцениваемого параметра распределения.
Доверительная вероятность – вероятность того, что доверительный интервал накроет действительное значение параметра, оцениваемого по выборочным данным.
Оценивание с помощью доверительного интервала – способ оценки, при котором с заданной доверительной вероятностью устанавливают границы доверительного интервала.
Пусть для генерального параметра a получена из опыта несмещенная оценка a*. Нужно оценить возможную при этом ошибку. Назначим достаточно большую вероятность β – такую, что событие с этой вероятностью можно считать практически достоверным, и найдем такое значение ε для которого

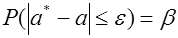
называемой уровнем значимости или риском. Уровень значимости часто выражают в процентах. Иначе формулу ( (5.8.1* ) можно интерпретировать как вероятность того, что истинное значение параметра а лежит в пределах
Вероятность β называется доверительной вероятностью, доверительным уровнем или надежностью, т.к. она характеризует надежность полученной оценки.
Интервал 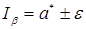
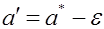
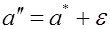
При этом отметим следующее. Ранее мы рассматривали вероятность попадания случайной величины на заданный (неслучайный) интервал. В данном случае дело обстоит иначе: величина ане случайна, зато случаен интервал I b . Случайно его положение на числовой прямой, определяемое его центром а * , случайна и длина интервала 2 e, так как величина e вычисляется, как правило, по опытным данным, т.е. по результатам эксперимента. Поэтому в рассматриваемом случае удобно толковать интервал I как вероятность того, что случайный интервал I b накроет величину а.
Величина доверительного интервала зависит от доверительной вероятности, с которой гарантируется нахождение параметра внутри доверительного интервала: чем больше величина β, тем больше и ε (т.е. с чем большей вероятностью мы хотим гарантировать полученный результат, тем в большем интервале он должен находиться).
Увеличение числа опытов проявляется в сокращении доверительного интервала при постоянной доверительной вероятности или в повышении доверительной вероятности при сохранении доверительного интервала.
ППри построении доверительного интервала решается задача об абсолютном отклонении:
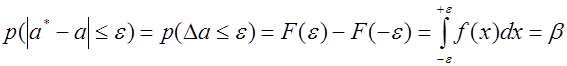
Таким образом, если известен закон распределения оценки a*, то задача определения доверительного интервала решается довольно просто.
Рассмотрим построение доверительного интервала для математического ожидания нормально распределенной случайной величины с известным генеральным стандартом σх.
Понятие генерального стандарта тесно связано с понятием точности прибора. Класс точности прибора – это выраженная в процентах относительная предельная погрешность измерения величины, равной пределу измерения прибора. В измерительной технике в большинстве отраслей промышленности под предельной погрешностью понимается величина, равная двум среднеквадратическим отклонениям
Пусть имеется выборка объема n значений случайной величины. Оценкой mx является среднее выборки:
Для построения доверительного интервала необходимо знать распределение этой оценки. Для выборок из генеральной совокупности, распределенной нормально можно показать, что 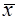
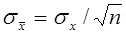
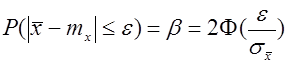
Задавшись доверительной вероятностью, определим по таблице значение функции Лапласа 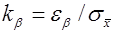
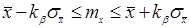
Из оценки видно, что уменьшение доверительного интервала обратно пропорционально квадратному корню из числа наблюдений. Следовательно, если надо уменьшить возможную ошибку в два раза надо увеличить число наблюдений в 4 раза.
Если закон распределения оценки не известен, то в математической статистике применяют обычно два метода:
1) приближенный – при n более 50 заменяют неизвестные параметры их оценками;
2) от случайной величины a * переходят к другой случайной величине, закон распределения которой не зависит от оцениваемого параметра а, а зависит только от объема выборки n и от вида распределения величины Х. Такого рода величины наиболее подробно изучены для нормального закона. В качестве доверительных границ берут симметричные квантили
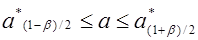
Если выразить через р,
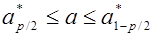
На практике, как правило, число измерений конечно и не превышает 10…30. При малом числе измерений фактическая дисперсия 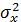
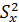
t – случайная величина, имеющая распределение, отличное от нормального, зависящее от числа степеней свободы(t – распределение или распределение Стьюдента). При больших значениях n распределение Стьюдента приближается к стандартному нормальному распределению. И, по аналогии, получаем построение доверительного интервала
Дата добавления: 2020-12-22 ; просмотров: 440 ; Мы поможем в написании вашей работы!
- чем больше длительность одного оборота оборотных средств
- чем больше докторов тем больше болезней значение пословицы